The development of information about whole numbers has been the emphasis of major current theories of numerical development, whereas the development of knowledge about other types of numbers, such as fractions and negative numbers has been relegated to secondary significance. To the degree that these concepts address the formation of knowledge of other types of numbers, it is usually to point out distinctions between their adoption and that of whole numbers, as well as to describe how whole number knowing impairs comprehension of them. Whole number learning is shown as radically different from and distinct from understanding other forms of numbers.
Definition
Whole numbers are the positive integers from 0 to infinity that are included in the number system. These figures can be found on the number line. As a result, they’re all genuine numbers. All whole numbers are real numbers, although not all real numbers are whole numbers, we can claim. As a result, whole numbers can be defined as the set of positive integers plus 0. The collection of whole numbers and negative natural numbers is known as integers. As a result, integers comprise both positive and negative numbers, as well as zero. Natural numbers, whole numbers, integers, and decimals are all forms of figures to make up real numbers. Whole numbers refer to the entire set of natural numbers, including ‘0.’
Examples
The following are some examples: 0, 110, 5, and 36, 999, 10200, 7, 99, 10, and so on.
The counter examples of whole numbers for the sake of better understanding are as follows
-1 , -100 , -6 , -5, -34, -99 , -12000 , -110, and so on are not whole numbers.
Symbol
Whole numbers are numbers that have no fractions and are made up of positive values and zero. The symbol for it is “W,” and the digits are 0 through 1, 2, 3, 4, 5, 6, 7, 8, 9,… .Nothing or a null value is represented by zero as a whole. Hence symbolically The set of whole numbers is as follows
W = {0, 1, 2, 3, 4…}
Relationship of whole numbers with other numbers
People frequently make the mistake of assuming that just because someone can count means they understand and can use numerical value relationships. That, however, is not the case. There is a huge gap between what people believe is required to learn can count and make logical sense of full numbers.
The principles or methods involved with counting and making sense of whole numbers and their relationships are listed below:
- Category
- Terms that are related are counted as one.
- Congruence
- One-on-one communication
- Numbers conservation
- Cardinality
- Counting in a structured manner
- Subsidize
The above list of concepts and techniques are required to count and build a strong understanding of whole number values and connections.
Hence, keeping in mind the above facts the whole numbers are related to natural numbers({1, 2, 3, …}), Real numbers, integers, positive integers rational numbers,
So, first of all listed the set in Roster notation
W = {0, 1, 2, 3, 4, … } ___________set of whole numbers
N = {1, 2, 3, 4, 5, 6, … } _________________set of natural numbers
Z = {…-3, -2, -1, 0, 1, 2, 3, … } _______________Set of integers
P = {2, 3,5, 7, 11, 13, 17, … } __________________set of prime numbers
O = {1, 3, 5, 7, 9, 11…} ___________________________set of odd numbers.
Let’s see graphically position of whole numbers.
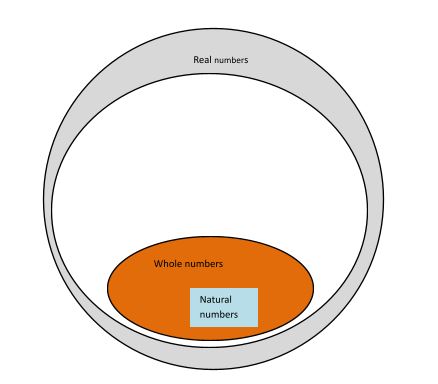
These are positive integers, including zero, without fractional or decimal portions (3/4, 2.2, or 5.3 are not whole numbers). On whole numbers, operations such as addition, subtraction, multiplication, and division are feasible. Hence, we conclude that
The alphabet ‘W’ in capital letters is used to indicate entire numbers.
W = 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, and so on.
As a result, the whole list of numbers contains 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12,…
Facts about whole numbers
- All whole numbers are real numbers
- All natural numbers are whole numbers
- All counting numbers are whole numbers
- All positive integers, including zero, are whole numbers
- Whole numbers never include negative numbers.
Number line representing whole numbers
A number line is a straight line with numbers put at regular spacing or sections along its course in mathematics. A number line can be drawn straight and can be extended in any dimension indefinitely. A number line representing whole numbers starts at 0 (Zero) and is marked 1, 2, 3, 4, 5, 6, 7, 8, … at equal distances on the right hand side of 0. As a result, a whole number on a number line has the following form:
0 1 2 3 4 5 6 …

The arrow-head on the right-hand side indicates that the complete numbers go on indefinitely.
Properties of whole numbers
Mathematical operations such as addition, deduction, division, and multiplication are used to define the properties of whole numbers. When two whole numbers are added or divided, the result is a whole number. Subtracting two whole numbers may or may not produce whole numbers, i.e., it can be an integer. Furthermore, in some circumstances, dividing two whole integers yields a fraction. Let us now look at some more properties of whole numbers and their demonstrations using examples.
Closure property
A set is closed for some arithmetic operations if it has the closure property. That really is, if the operation can always be performed with elements inside the set, then set is closed with respect to that operation. As a result, a set is either closed or open with regard to a certain operation. If x or y are two whole numbers, then x. y or x + y is also a whole number.
Hence, closure property hold in whole numbers with respect to addition as well as multiplication operation.
For example
2 and 3 are whole numbers/
2+3 = 5
5 is also a whole number hence it is closed with respect to addition.
Hence we generalize this property
Let,
a, b belongs to whole numbers then
a+ b = c is also whole number.
Now, let’s see for multiplication
Let 2 and 8 are whole numbers then
2 × 8 = 16
16 is also whole number.
Hence whole numbers also closed with respect to multiplication.
We can generalize this property for whole set of whole numbers is as follows
Let a and b are whole numbers
Then a × b = c
C is also closed.
Note: closure property does not hold for division and subtraction operations.
We prove this statement by the following result
Let 2 and 9 are whole numbers then
2-9 = -7 but -7 is not whole number that’s why it is not closed for subtraction.
Similarly when we divide two whole numbers in some cases their answers are not whole numbers for example, 5/2 =2.5it is not whole number.
Commutative property
The commutative property says that the values we work with can be changed or switched from their original positions without affecting the result. The characteristic applies to addition and multiplication, but not subtract or division. If two whole numbers are combined or multiplied in any order, both sum and output would be the same, i.e., if x and y represent two whole numbers, then x + y = y + x and x. y =
Example
Consider the numbers 4 and 10 as an example.
Let a = 4 b = 10
a + b = 4+10
= 14 —————– (1)
b + a = 10 + 4
=14 —————— (2)
Hence, equation (1) and (2) shows that
a + b = b + a
Hence it is commutative with respect to addition according to the definition of commutative property.
Now, let’s check the result for the multiplication operation
Let a = 5 b = 15
a × b = 5 × 15
= 75 ————— (A)
b × a = 15 × 5
= 75 —————- (B)
Hence , from equation (A) and (B) it is proved that whole numbers satisfy the commutative by the definition of commutative property
The commutative property with respect to addition and multiplication
As a result, when it comes to algebraic, whole numbers are commutative.
Additive identity
Additive identity refers to a characteristic of numbers that is used in adding operations. It’s the number that, when multiplied by another, yields the number on its own. ‘When a value is added to zero, it gives the very same number,’ says the characteristic. The identity element is referred to as ‘zero’ (also known as additive identity). When we multiply any integer by zero, the outcome is the same number. If x is a complete number, then 0+x = x +0
If ‘a’ can be any whole number, then
0 + a = a + 0 = some whole number.
For Example:
- 2+0 = 2
0+ 2 = 2
- 45 + 0 = 45
0 + 45 = 45
As a result, 0 is known as the whole number’s additive identity.
Multiplicative identity
The multiplicative identity property asserts that when a number is multiplied by one, the output, or product, is the same as the previous value. If a whole number is multiplied by one, its value remains the same; for example, if x is a whole number, x.1 = x = 1.x
For Example:
1 ×5 = 5
115 × 1 = 115
98 × 1 = 98
Here, also notice that 98 × 1 = 1 × 98 = 98
As a result, whole numbers have a multiplicative identity of 1.
Associative property
First of all we define associative property then we will apply on the set of whole numbers and see either it is hold or not for whole numbers.
Whenever three or even more numbers are added (or multiplied), this characteristic indicates that the sum (or result) is the same regardless of how the addends are grouped (or the multiplicands).
The use of parenthesis or brackets to group numbers is known as grouping.
Three or more numerals are involved in the associative characteristic.
The numbers included in a parenthesis or bracket is treated as a single unit. Just addition and multiplication, not subtraction or division, can be employed with the associative attribute. When adding or multiplying numerous numbers, the associative characteristic comes in handy. We may break down the problem into smaller pieces by grouping them together. It simplifies and speeds up multi-number addition and multiplication calculations.
X + (Y + Z) = (X + Y) + Z
Let us suppose three whole numbers
X =6 y = 9 z = 5
X+(Y + Z) = 6 + (9 + 5)
= 6 + 14
= 20 ————- (i)
(X + Y) + Z = (6 + 9 ) + 5
= 15 + 5
= 20 ——————— (ii)
Hence from equation (i) and (ii) shows that associative property hold in the set of whole numbers.
Let’s solve one more example of associative property
A = 0 B = 6 c = 100
A + (B + C) = 0 + (6 + 100)
= 0 + 106
= 106
(A + B) + C
= (0 + 6) + 100
= 6 + 100
= 106
Hence it is hold for any whole numbers.
Fact: The term “associative property” derived from the term “associate,” which refers to the gathering of numbers.
Distributive property
To “distribute” anything is to split it or to provide a piece or part of it.
Simply multiply the sum of two or even more addends by a number produces the very same result as multiplication each addend individually by the number and then combining the products collectively, according the distributing property. Symbolically,
A × (B + C ) = (A × B)+ ( A × C)
Now we check it for the whole numbers either it is hold in it or not.
Let A = 2 B = 4 C = 7
A × (B + C) = 2 × (4 + 7)
= 2 × 11
= 22 ————- (1)
( A × B ) + ( A × B) = ( 2 × 4) + (2 × 7)
= 8 + 14
= 22 ————- (2)
Hence from equation 1 and 2it is proved that distributive property satisfied in whole numbers.
Multiplication by zero
In the field of mathematics, zero is a peculiar companion. It does not adhere to the same set of rules like the other number. It has its own set of characteristics that enable it to make arithmetic more engaging. The multiplication property is one of zero’s unique rules. The combination of any number and zero is zero, according to the multiplication property. It makes no difference what the value is; if you multiply it by zero, you get “ 0 ”.
If a whole number is multiplied by 0 it always equals 0, i.e. x.0 = 0.x = 0
Example:
11 = 11 × 0
= 0
= 0 × 11
= 0
1465678 × 0 = 0
5 × 0 = 0
In this case, 0 × 12 = 12 × 0 = 0
As a result, any whole integer multiplied by 0 always equals 0.
Dividing by zero
The division of a whole number by o isn’t specified, so if x is just a whole number, x/0 isn’t either.
Let a belongs to whole numbers
a/0 = infinity
What’s the Difference Between Whole and Natural Numbers?
| Whole numbers | Natural numbers |
| Set of whole numbers = { 0, 1, 2, … } | Set of natural numbers = { 1, 2, 3, …} |
| The count begins at zero. | The count begins at zero. |
| Natural numbers are not always whole numbers. | Natural numbers are all integers. |
Is it possible for Whole Numbers to be negative?
It’s impossible for the total to be negative!
Whole numbers are defined as zero, one, two, three, four, five, six, seven, and so on until positive infinity. Negative numbers have no place in this world.
Is the number 0 a whole number?
The collection of all natural numbers, including zero, is known as whole numbers. So, sure, 0 (zero) is a whole number, and it is also the first whole number.
Conclusion:
Number is the initial content area, which includes whole numbers, procedures, and relationships. The fundamental purpose of many early childhood programmes is to teach children how to work with numbers. Children, on the other hand, are capable of demonstrating competency in more sophisticated mathematics activities including whole numbers operations and relations when given the opportunity. Cardinality, for example, is an important aspect of children’s number learning since it tells them how many items are in a set. Understanding numbers extends to relations and operations. The relation core consists of skills like constructing greater than, less than, and equal to relations. Additive inverse are two of the most important processes.









