Introduction
In the realm of mathematics, addition is a fundamental operation that allows us to combine two or more numbers. Two widely used techniques to teach addition are number bonds and fact families. These methods provide an intuitive and efficient approach to understanding and solving addition problems.
Required Knowledge
Basic arithmetic: Understanding the concepts of addition and subtraction is essential for using number bonds and fact families effectively.
Commutative property of addition: The commutative property states that the order of numbers in an addition equation does not affect the sum (a + b = b + a). This property is fundamental to understanding fact families.
The inverse relationship between addition and subtraction: Recognizing that addition and subtraction are inverse operations helps learners comprehend the connection between the equations in a fact family.
Grade Appropriateness
Number bonds are introduced to children for the first time in the Foundation Stage (about age 4) without being specifically referred to as such.
Children are merely dividing groups of items into two groups at this point. They then use tools or markers they have created to assist them in breaking down small numbers (often up to 5) into smaller numbers.
Children develop their bank of memorized number bonds throughout key stage 1 (ages 5-7) and learn to apply them to solve math problems.
The idea of a fact family or fact families is one of the more often taught ideas in first-grade math, where children learn the fundamentals of addition and subtraction. Fact families help children comprehend the relationships between numbers and the reasoning behind addition and subtraction.
Definition
Number Bonds: Number bonds are visual representations that help to break down a number into its parts. Number bonds illustrate the relationship between a whole number and its parts, making it easier to understand and solve addition problems.
Fact Families: Fact families are sets of addition and subtraction equations that demonstrate the relationship between numbers. They help students understand the relationship between addition and subtraction and the commutative property of addition on a deeper level.
Key Steps
Number Bonds:
a. Identify the whole number and its parts: Begin by identifying the whole number and its parts, which will be used to create a number bond diagram.
We have 2, 3, and 5. 5 is a whole number, while 2 and 3 are the pairs that makeup 5.

b. Create a number bond diagram: Draw a circle or any other shape representing the whole number. Then, draw lines from the circle to two or smaller circles or shapes representing the parts.
The diagram below shows a number bond of 5.

c. Write the addition sentence: Write an addition sentence using the numbers from the number bond diagram to express the relationship between the whole number and its parts.
Here, the number 5 can be considered the sum of 2 and 3. It can be modeled using number bonds in the manner shown below. The order of the terms does not matter because addition is commutative. The addition sentences that follow are a result.

Fact Families:
a. Choose three numbers: Select a set of three numbers, with two smaller numbers that add up to the larger number.
b. Write the addition sentences: Write two addition sentences using the three chosen numbers, demonstrating the commutative property of addition.
c. Write the subtraction sentences: Write two subtraction sentences using the same three numbers, illustrating the inverse relationship between addition and subtraction.
The diagram below shows the three numbers, 3, 7, and 10, with two addition sentences and two subtraction sentences using these numbers. These sentences illustrate the inverse relationship between addition and subtraction.

Properties
Number Bonds:
a. Part-Part-Whole Relationship: Number bonds illustrate the part-part-whole relationship, where the whole number is the sum of its parts.
b. Flexibility: Number bonds can be adapted to represent various combinations of numbers that make up the whole, allowing for a comprehensive understanding of addition.

Fact Families:
a. Commutative Property: Fact families showcase the commutative property of addition, as demonstrated by the two addition sentences with interchanged addends.
b. Inverse Relationship: Fact families highlight the inverse relationship between addition and subtraction, as the two subtraction sentences involve the same numbers as the addition sentences.
In the illustration below, 3, 5, and 8 make a fact family. There are two addition facts and two subtraction facts in this fact family.

Examples
Example 1
Find 4+__=10.
Solution:
The pairings that make up the number bonds for the whole number 10 are as follows:

From here, we know that 4 and 6 make 10. Hence, 4+6=10.
Example 2
Write two addition and two subtraction sentences for the fact family illustrated below.

Solution:
The numbers 4, 8, and 12 form a fact family. The addition and subtraction sentences are as follows:
Addition Sentences: 8 + 4 = 12 and 4 + 8 = 12.
Subtraction Sentences: 12 – 4 = 8 and 12 – 8 = 4.
Example 3
Use a fact family triangle for each group of numbers and create addition and subtraction sentences.

Solution:
The fact family must be built using the numbers given in each group and placed in the triangle. The two smaller numbers add up to the larger number.

Example 4
Matthew has four green buttons, while Maria has five blue buttons. How many buttons do they have in all?
Solution:
The number bond below gives a clear visual writing of the correct addition sentence or equation to find the answer.
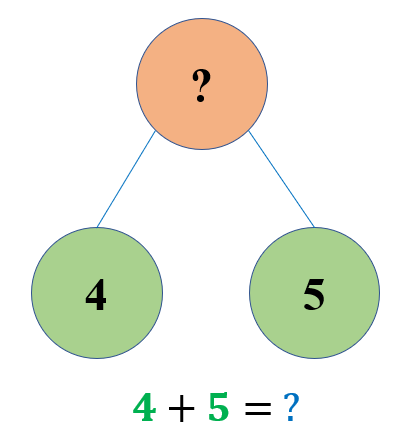

Therefore, Matthew and Maria have nine buttons in total.
Example 5
How many possible number bonds are there in 7?
Solution:
The diagram below shows how many possible number bonds there are in 7.

The addition sentences or equations for 7 are:
0 + 7 = 7
1 + 6 = 7
2 + 5 = 7
3 + 4 = 7
By commutative property, the parts can be switched; hence the addends can be written in any order.
7 + 0 = 7
6 + 1 = 7
5 + 2 = 7
4 + 3 = 7
Therefore, there are four possible number bonds in 7.
Frequently Asked Questions
What distinguishes fact families from number bonds?
Number bonds are visual representations that help break down a number into its parts, while fact families are sets of related addition and subtraction equations demonstrating the relationship between numbers.
Where can fact families be used?
Fact families are used to helping children remember the fundamental addition and subtraction facts as well as to reinforce or learn the relationship between addition and subtraction.
How to construct number bonds?
Circles and lines are used to represent number bonds. The first circle contains the “whole,” whereas the remaining two circles include the “parts.”

What distinguishes number bonds from number facts?
One of the various kinds of number facts is number bonds. As two numbers are added together to create a third, number bonds can be addition number facts. On the other hand, number facts can be used for addition, subtraction, multiplication, and division.
Why do we use number bonds?
Number bonds can be a very effective math technique. They can be applied to aid in the speedy recognition of number facts. The two parts of a number bond are added to find the whole if the total is missing. If one of the parts is missing, the missing part can be found by deducting one of the other parts from the whole.
Number bonds facilitate the practical breakdown of numbers. They assist children in visualizing and quickly resolving addition and subtraction problems.
Recommended Worksheets
Number Bonds to 100 (Winter Themed) Math Worksheets
Number Bonds: Word Problems (World Animal Day Themed) Math Worksheets
Addition of Numbers using Number Bond and Fact Families (Arcade Themed) Math Worksheets









