Introduction
Any structure, open or closed, with a specific shape and characteristics composed of lines, curves, and points is referred to as a geometric shape. The following are some examples of well-known geometric shapes: square, rectangle, circle, cone, cylinder, sphere, etc. These shapes are all distinct from other shapes and have specific characteristics in common.
Geometric shapes are the figures used in mathematics to represent the shapes of real-world objects. Shapes are the forms of things in geometry that have surfaces, angles, and boundary lines. There are several types of both 2D and 3D shapes.
Simple geometric figures with a defined boundary, inner surface area, and outside surface area are what constitute shapes. We may learn about different shapes and their characteristics through geometry. Basic shapes and terminologies are used to introduce geometry to students.
It is crucial that we gain the necessary comprehension of geometric shapes before turning our attention to the more complex and competitive mathematical ideas of geometry and algebra. This article will teach you about fundamental geometric shapes and their characteristics.
What are Geometric Shapes?
Definition
Geometric shapes are defined as being enclosed by a boundary made up of a specific number of curves, points, and line segments. Every shape has a distinctive name, such as a circle, square, triangle, or rectangle.
Any object with a definite structure qualifies as a geometric shape. Lines, curves, angles, and surfaces make up the shapes in these figures. Square, rectangle, circle, cylinder, cylinder, cube, sphere, and other familiar geometric shapes are just a few. A polygon is a geometric shape having three sides or more. Common polygons include triangles, squares, rhombuses, trapezoids, etc.
In everyday life, simple geometric shapes exist. For example, a pizza slice is shaped like a triangle, a television screen is typically rectangular, and a ball has a sphere shape, among other things.
The figures representing various objects’ shapes are known as geometrical shapes. While some figures are three-dimensional shapes, some are two-dimensional figures. Three-dimensional shapes are located on the x, y, and z axes, while two-dimensional figures only exist on the x and y axes.
Starting with a line, a curve, or a line segment allows you to create geometric shapes. A triangle is a figure where three-line segments are joined, and a pentagon and other shapes and figures can be made based on the number and arrangement of these lines.
Types of Geometric Shapes
Geometric shapes are the figures used in mathematics to represent the shapes of real-world objects. Shapes are the forms of things in geometry that have surfaces, angles, and boundary lines. There are several types of both 2D and 3D shapes.
Two-Dimensional Shapes ( 2D Shapes )
Two-dimensional (2D) shapes are flat shapes that lack height or thickness. The only parameters are length and width. Circles and polygons, like triangles, squares, rectangles, etc., are a few examples of 2D shapes.

Shapes have characteristics that make it possible for us to identify them as such. Several shapes can exist depending on the number of a shape’s sides and corners. A two-dimensional (2D) shape’s corner is where two sides meet. A side is a straight line. An angle is formed since a vertex is another word for a corner. The shape below shows that it has four sides, four corners, and four angles.
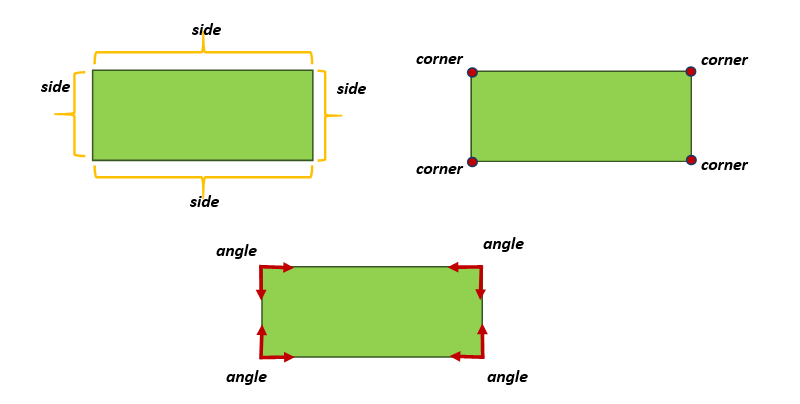
The equal length of a shape’s sides serves as a description. Equal-length sides are denoted with a hatch mark (“|”). The figure below shows how the opposite sides are equal in length. The measurements of the sides with a single hatch mark and the sides with two marks are different.

The typical 2D shapes and their properties are displayed below.
Circle
In two dimensions, a circle is a curved, non-cornered shape. Radius, diameter, circumference, and other me
trics are some of its attributes.
- A circle has neither sides nor edges. It is circular.
- The distance encircling a circle is known as its circumference.
- The radius is the distance from a circle’s centre to any point on the circle.
The diameter is the line segment with two endpoints on the circle that travels through its centre.
Polygons
Polygons are two-dimensional shapes with a defined number of sides. Triangles, parallelograms, squares, rectangles, rhombuses, kites, and trapezoid
s are a few polygons with equal sides and angles.
Polygons have different names in line with the properties that define them, such as the number of sides, edges, corners, and angles.
Triangle
Triangles are three-sided polygons. Triangles can be categorized as scalene, isosceles, or equilateral based on the lengths of their sides. Triangles can be acute, obtuse, or right, depending on their angles.

A triangle’s internal angles sum to 180 degrees. Acute triangles have angles that are all less than 90 degrees. One side of a right triangle is 90 degrees in angle. One of the angles of obtuse triangles is greater than 90 degrees.
Quadrilaterals
The terms “quad” (four) and “lateral” (side) are where the term quadrilateral originated. The quadrilateral family of shapes consists of four sides, four vertices, and four angles. Each quadrilateral shape differs slightly from the others in a number of ways. The list below are examples of quadrilaterals and their properties:
Parallelogram
The four sides and four corners of a parallelogram are made up of parallel lines. A parallelogram has parallel opposed sides but not necessarily equal angles. The three different kinds of parallelograms are square, rectangle, and rhombus.

The blue line segment shows the opposite sides of the parallelogram.
Square
There are four sides and four corners to a square. Equal-length sides make up the square. A square is made up of two parallel sets of sides.
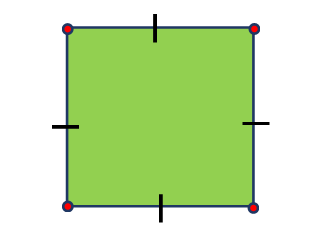
The red dots stand in for the square’s four corners.
The hatch markings indicate the equal length of the sides.
Rectangle
There are four sides and four corners to a rectangle. The lengths of the two opposite side pairs in a rectangle are equal. The two sets of sides of a rectangle are parallel.
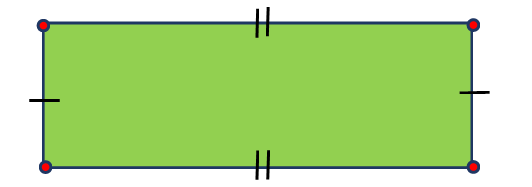
Red dots indicate the rectangle’s four corners.
The hatch marks indicate that the lengths of opposite sides are equal.
Rhombus
Diamonds are another name for rhombuses. Four sides and four corners make up a rhombus. A rhombus looks like a tilted square. The length of the sides is the same. There are parallel opposing sides to a rhombus.
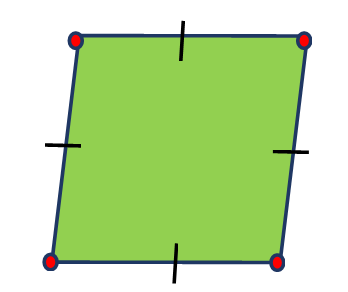
The hatch marks show the rhombus’s equal-length sides.
The red dots stand in for the corners of the rhombus.
Kite
Four sides and four corners make up a kite. Two pairs of sides on a kite are the same length.
A kite can never have parallel sides.
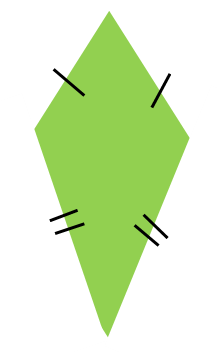
The hatch marks show the rhombus’s equal-length sides.
Trapezoid
A trapezoid has just one set of parallel sides. (In India and Britain, they use the word “trapezium”)
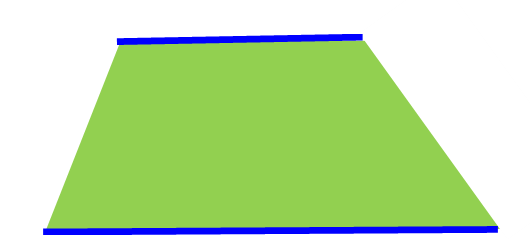
The parallel opposite sides are shown in blue line segments.
Polygons with more than four sides
Here are a few examples of polygons that have more than four sides.
Pentagon
The pentagon is a shape with five sides of equal length. Its inner angles are equivalent to 540 degrees in total—each 108 degrees in a regular pentagon’s angles.
Hexagon
Hexagons are polygons having six sides. The sum of its inner angles is 720 degrees. In a regular hexagon, each angle is 120 degrees.
Heptagon
Polygons having seven sides are referred to as heptagons. A heptagon’s interior angles add up to 900 degrees. Each vertex of a regular heptagon has an angle of 128.57 degrees.
Octagon
A polygon with eight sides is called an octagon. There are 1080 total interior angles. In a regular octagon, each angle is 135 degrees in measure.
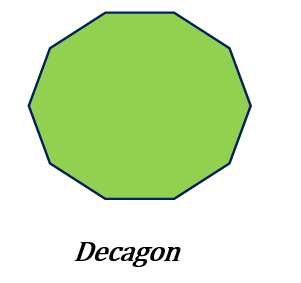
Decagon
Ten-sided polygons are referred to as “decagons”. Its inner angles add up to 1440 degrees in total. Each angle on a regular decagon has 144 degrees.
Three-Dimensional Shapes ( 3D Shapes )
Three-dimensional (3D) shapes take up space. They have three dimensions length, height, and width. We can hold three-dimensional objects, such as a pencil, phone, table, etc.
All three-dimensional shapes share properties. Among these properties are faces, edges, and corners. A flat surface makes up the face of a three-dimensional shape. The faces frequently take on 2D shapes. The edge of a surface is the line dividing two of its surfaces
A 3D shape’s corner is formed when two or more of its edges meet together. A vertex is another name for a corner, as it is for 2D objects.
Here are some typical 3D shapes, along with brief descriptions of each.
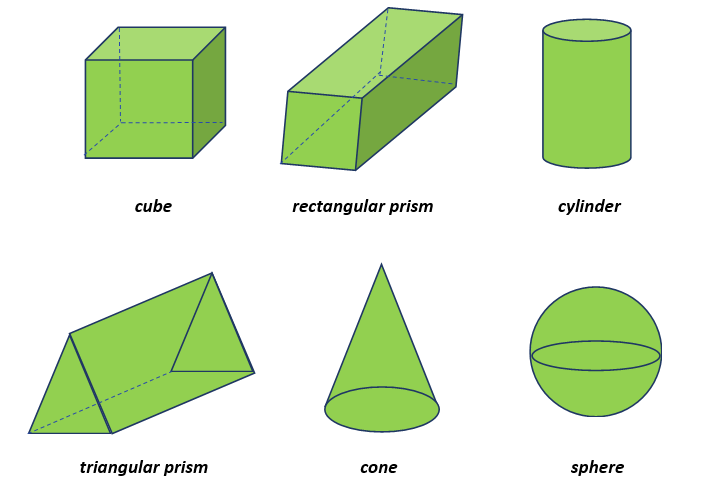
Cube
There are six identical faces on a cube. A cube has squares on each of its faces. There are 12 edges on it with eight corners. The faces, edges, and corners are all the same size and length.
Rectangular Prism
There are six faces on a rectangular prism. A rectangle makes each face. The size of the opposite faces is constant. It has 12 edges and eight corners.
Triangular Prism
A triangular prism has five faces. It features three rectangle-shaped faces and two triangle-shaped faces. The sizes of the two triangular faces are the same. It has six corners and nine edges.
Cylinder
A cylinder has a tube in the middle and two circles of the same size on each end. It features one curved surface and two flat faces. A cylinder has two edges and no corners.
Cone
At the base of a cone is a circle, and at the other end is a point. There is one flat face and one curved surface. A cylinder has a single edge without any corners.
Sphere
A spherical shape has the ideal roundness. The surface of it is curved. A sphere does not have flat faces, edges, or corners. The distance between each point and centre is constant on the sphere.
List of Geometric Shapes
The tables below show the geometric shapes, types, and properties list.
Lists of Two-dimensional Geometric Shapes
List of Geometric Shapes ( Triangles )
| Name | Illustration | Type | Vertices | Edges |
| Equilateral Triangle | 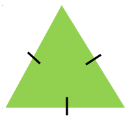 | Two-dimensional | 3 | 3 |
| Isosceles Triangle | 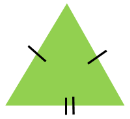 | Two-dimensional | 3 | 3 |
| Scalene Triangle | 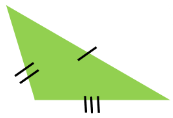 | Two-dimensional | 3 | 3 |
| Right Triangle | 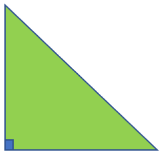 | Two-dimensional | 3 | 3 |
| Obtuse Triangle |  | Two-dimensional | 3 | 3 |
| Acute Triangle | 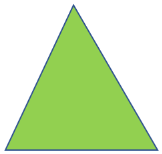 | Two-dimensional | 3 | 3 |
List of Geometric Shapes ( Quadrilaterals )
| Name | Illustration | Type | Vertices | Edges |
| Square |  | Two-dimensional | 3 | 3 |
| Rectangle |  | Two-dimensional | 3 | 3 |
| Rhombus |  | Two-dimensional | 3 | 3 |
| Parallelogram |  | Two-dimensional | 3 | 3 |
| Trapezoid |  | Two-dimensional | 3 | 3 |
| Kite |  | Two-dimensional | 3 | 3 |
List of Geometric Shapes ( Polygons with a specific number of edges )
| Name | Illustration | Type | Vertices | Edges |
| Pentagon | 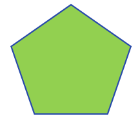 | Three-dimensional | 5 | 5 |
| Hexagon |  | Three-dimensional | 6 | 6 |
| Heptagon | 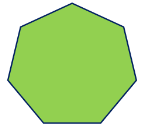 | Three-dimensional | 7 | 7 |
| Octagon | 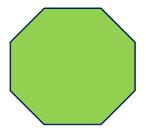 | Three-dimensional | 8 | 8 |
| Decagon |  | Three-dimensional | 10 | 10 |
List of Three-dimensional Geometric Shapes
List of Geometric Shapes ( 3D )
| Name | Illustration | Type | Vertices | Edges | Faces |
| Cube | 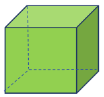 | Three-dimensional | 8 | 12 | 6 |
| Cuboid | 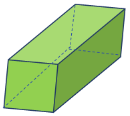 | Three-dimensional | 8 | 12 | 6 |
| Cone |  | Three-dimensional | 1 | 1 | 2 |
| Cylinder |  | Three-dimensional | 0 | 2 | 3 |
| Sphere |  | Three-dimensional | 0 | curved | 1 |
Summary
Geometric shapes are defined as being enclosed by a boundary made up of a specific number of curves, points, and line segments. Every shape has a distinctive name, such as a circle, square, triangle, or rectangle.
Any object with a definite structure qualifies as a geometric shape. Lines, curves, angles, and surfaces make up the shapes in these figures. Square, rectangle, circle, cylinder, cylinder, cube, sphere, and other familiar geometric shapes are just a few. A polygon is a geometric shape having three sides or more. Typical polygons include triangles, squares, rhombuses, trapezoids, etc.
List of Geometric Shapes and their Properties
2D Shapes
List of Geometric Shapes ( Triangles )
| Name | Type | Vertices | Edges |
| Equilateral Triangle | Two-dimensional | 3 | 3 |
| Isosceles Triangle | Two-dimensional | 3 | 3 |
| Scalene Triangle | Two-dimensional | 3 | 3 |
| Right Triangle | Two-dimensional | 3 | 3 |
| Obtuse Triangle | Two-dimensional | 3 | 3 |
| Acute Triangle | Two-dimensional | 3 | 3 |
List of Geometric Shapes ( Quadrilaterals )
| Name | Type | Vertices | Edges |
| Square | Two-dimensional | 3 | 3 |
| Rectangle | Two-dimensional | 3 | 3 |
| Rhombus | Two-dimensional | 3 | 3 |
| Parallelogram | Two-dimensional | 3 | 3 |
| Trapezoid | Two-dimensional | 3 | 3 |
| Kite | Two-dimensional | 3 | 3 |
List of Geometric Shapes ( Polygons with edges greater than 4 )
| Name | Type | Vertices | Edges |
| Pentagon | Three-dimensional | 5 | 5 |
| Hexagon | Three-dimensional | 6 | 6 |
| Heptagon | Three-dimensional | 7 | 7 |
| Octagon | Three-dimensional | 8 | 8 |
| Decagon | Three-dimensional | 10 | 10 |
3D Shapes
List of Geometric Shapes ( 3D )
| Name | Type | Vertices | Edges | Faces |
| Cube | Three-dimensional | 8 | 12 | 6 |
| Cuboid | Three-dimensional | 8 | 12 | 6 |
| Cone | Three-dimensional | 1 | 1 | 2 |
| Cylinder | Three-dimensional | 0 | 2 | 3 |
| Sphere | Three-dimensional | 0 | curved | 1 |
Frequently Asked Questions on List of Geometric Shapes ( FAQs )
How do 2D and 3D geometric shapes differ from one another?
Two-dimensional (2D) shapes are flat shapes that lack height or thickness. The only parameters are length and width. Circles and polygons, like triangles, squares, rectangles, etc., are a few examples of 2D shapes. Some examples of 2D shapes include the following:
Circles
Triangles
Quadrilaterals ( Square, Rectangle, Parallelogram, Rhombus, Kite, and Trapezoid )
Polygons like pentagons, hexagons, heptagons, octagons, nonagons, and decagons
Three-dimensional (3D) shapes take up space. They have three dimensions length, height, and width. Three-dimensional shapes are objects we can hold, such as a pencil, phone, table, etc.
All three-dimensional shapes share properties. Among these properties are faces, edges, and corners. A flat surface makes up the face of a three-dimensional shape. The faces frequently take on 2D shapes. The edge of a surface is the line dividing two of its surfaces. A 3D shape’s corner is formed when two or more of its edges meet together. A vertex is another name for a corner, as it is for 2D objects.
The following are examples of 3D shapes:
Cube, Prisms, Cones, Cylinder and Sphere
What distinguishes regular shapes from irregular shapes?
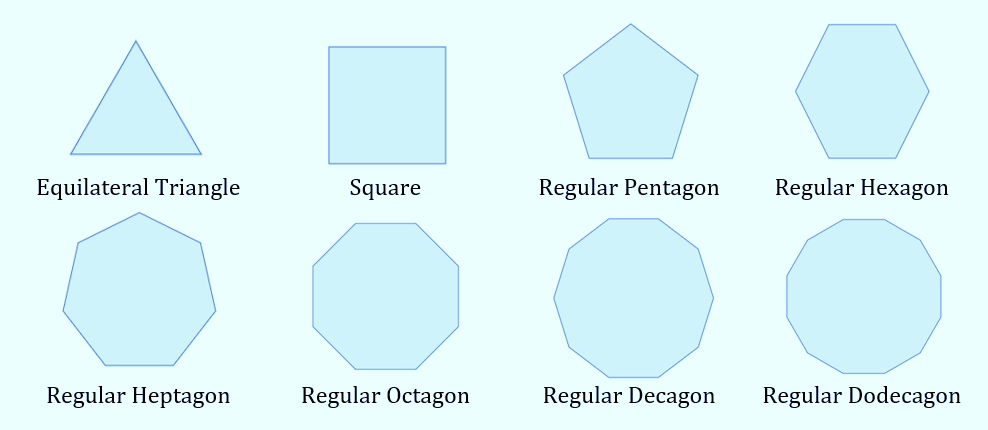
A regular shape is a two-dimensional (2D) shape whose (interior) angles and sides all have the same measurements.
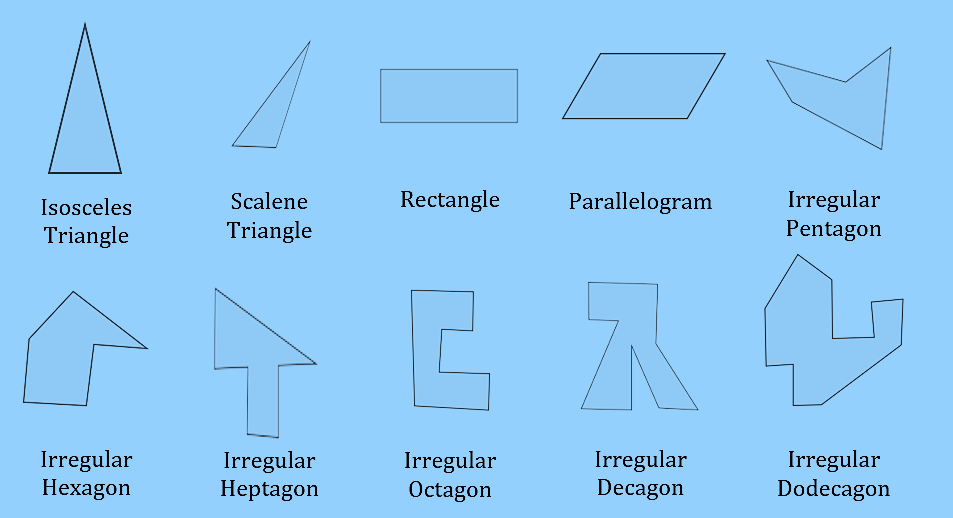
An irregular shape has sides and angles of any length and measurement. An irregular shape’s number of straight sides is sometimes used to decide its name. A shape is irregular, even if only one side has a different measurement.
The following are examples of regular shapes.
The following are examples of irregular shapes.
What are examples of geometric shapes in math?
There are many geometric shapes based on their properties. The following are some examples of basic two-dimensional (2D) and three-dimensional (3D) shapes:
Examples of 2D shapes:
Circle
Triangle
Square
Rectangle
Rhombus
Kita
Pentagon
Examples of 3D shapes:
Cube
Cuboid
Cone
Cylinder
Sphere
What are the basic polygons?
Two-dimensional (2D) shapes are flat shapes that lack height or thickness. The only parameters are length and width. The basic polygons include the following:
Triangle ( three edges )
Quadrilaterals ( four edges – like square, rectangle, rhombus, etc. )
Pentagon ( 5 edges )
Hexagon ( 6 edges )
Heptagon ( 7 edges )
Octagon ( 8 edges )
Decagon ( 10 edges )
Is a circle a polygon?
Polygons are two-dimensional geometric shapes with a fixed number of sides. Sides of polygons are connections of straight line segments from end to end.
Therefore, a circle is not a polygon since it is created using curves.
What are the different types of triangles?
Triangles are three-sided polygons. Triangles can be categorized as scalene, isosceles, or equilateral based on the lengths of their sides. Triangles can be acute, obtuse, or right, depending on their angles.
A triangle’s internal angles sum to 180 degrees. Acute triangles have angles that are all less than 90 degrees. One side of a right triangle is 90 degrees in angle. One of the angles of obtuse triangles is greater than 90 degrees.
What are examples of curved shapes?
Curved shapes are geometrical shapes that are made out of curved lines and related points. The following are examples of curved shapes.
| Circle This shape has only one curving line and no other linking or apex points.  | Oval/ Ellipse While it resembles a circle, the distance between the centre and the circumference is continually changing. Therefore, this shape has two axes, a major axis and a minor axis, and an elongated shape.  |
| Lens This shape resembles an ellipse but is made up of two different curving lines that come together at the ends. 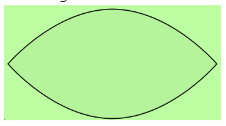 | Crescent The existence of two curving lines—one convex and the other concave—define this shape.  |
What are the different types of quadrilaterals?
The terms “quad” (four) and “lateral” (side) are where the term quadrilateral originated. The quadrilateral family of shapes consists of four sides, four vertices, and four angles. Each quadrilateral shape differs slightly from the others in a number of ways. The list below are examples of quadrilaterals and their properties:
| Square There are four sides and four corners to a square. Equal-length sides make up the square. A square is made up of two parallel sets of sides.  | Rectangle There are four sides and four corners to a rectangle. The lengths of the two opposite side pairs in a rectangle are equal. The two sets of sides of a rectangle are parallel.  |
| Parallelogram Parallel lines create a parallelogram’s four sides and four corners. A parallelogram’s opposite sides are parallel, but the angles may not be the same. Square, rectangle, and rhombus are the three diverse types of parallelograms.  | Rhombus Rhombuses can also be referred to as diamonds. A rhombus has four sides and four corners. A rhombus resembles a square tilted to the side. The sides are the same length. A rhombus has parallel opposing sides.  |
| Kite A kite has four sides and four corners. A kite has two sets of sides that are the same length.Parallel sides are never possible for a kite.  | Trapezoid There is only one set of parallel sides in a trapezoid. (They say “trapezium” in India and Britain)  |
What are examples of geometric shapes in real life?
The following are examples of 2D and 3D geometric shapes in real life
| Name | Type | Examples |
| Circle | 2D | cookies, wheels, pies, plates |
| Triangle | 2D | slice of pizza, sails on a boat, tortilla chips |
| Square | 2D | chessboard, square tiles |
| Rectangle | 2D | paper bills, frames, book cover |
| Pentagon | 2D | traffic signs |
| Hexagon | 2D | snowflakes, beehive cells |
| Octagon | 2D | stop signs |
| Cube | 3D | six-sided dice, sugar cubes |
| Sphere | 3D | basketball, marbles, planets |
| Cones | 3D | party hats, traffic cones, waffle cones |
| Cylinder | 3D | drinking glasses, cans, pipes |
Recommended Worksheets
Regular and Irregular Shapes (World Oceans Day Themed) Math Worksheets
Basic Shapes (International Day of PWD’s Themed) Math Worksheets
Symmetrical Shapes (Bodhi Day Themed) Math Worksheets









