Introduction

To study the unit circle and learn about its properties and importance in mathematics, let us first recall what a circle is. We have learnt that a circle is a type of shape. It is a two-dimensional figure formed by a set of points that are at a constant or at a fixed distance from a fixed point in the plane. This fixed distance is called the radius of the circle and the fixed point is called the centre of the circle.

Parts of a Circle

Circumference – The circumference of a circle is the distance around the boundary of the circle. In other words, it is the perimeter of the circle.

Radius – Radius is the distance from the centre of a circle to any point on the boundary of the circle. 

Diameter – Diameter is the line from one point on the boundary of the circle to another point and passing through the centre of the circle. It is twice the length of the radius.

Chord of a Circle – The chord of a circle is the line from one point on the boundary of the circle to another point. The diameter is the longest chord of a circle.

In the circle above, O is the centre of the circle.

The line segment AO is the radius of the circle.

The lone segment PQ is the diameter of the circle. Note that the line segment PQ is passing through the centre O

The line segment AQ is a chord of the circle that joins two points A and Q that lie on the boundary of the circle.

The curve formed by AQ is the arc of the circle.

A type of circle is the unit circle. Let us find out what do we mean by a unit circle?

Definition:

The meaning of unit, as we all know is 1. Therefore it can easily be made out that a unit circle is a circle with a radius of 1. The following figure represents the circle with the radius as 1 unit. We have learnt in the circle that that radius and the centre are two important components for studying circles. So, how do we define the values of the centre and the radius of the unit circle? Let us find out.

Radius of the Unit Circle

By the very definition of the unit circle, it is clear that the radius of the unit circle is always one unit.

Centre of the Unit Circle

 We now know that by definition, the radius of the unit circle is always 1. Where does the centre of the unit circle lie? Can it be any point on the Cartesian Coordinate Plane or it is also fixed like the radius of the unit circle?

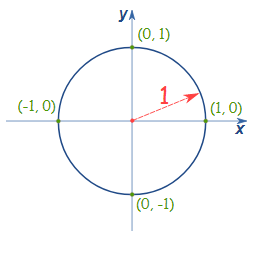
The centre of the unit circle just like its radius is a fixed point. The centre of the unit circle is the point of origin, i.e. ( 0, 0 ).

Equation of a Unit Circle

The equation of the circle is derived from the equation of the circle and it has all the properties of the circle. In other words, the equation of a unit circle is represented using the second-degree equation with two variables x and y. 

We know that the general equation of a circle is given by

( x – a )² + ( y – b )² = r², where,

The centre of the circle is given by the point ( a, b ) and the radius of the circle is r.

Now, we will use the above equation to derive the general equation of the unit circle.

We have just learnt that the radius of the unit circle is one unit while the centre of the unit circle lies at the point of origin, i.e. (1, 1 )

Therefore, for the above equation, in case of unit circle,

r = 1 and ( a, b ) = ( 0, 0 )

Substituting these values of ( a, b ) and r in the above equation, we will get

( x – 0 )² + ( y – 0 )² = 1²

⇒ x² + y²  =1

Now we have understood what a unit circle is. But, the question arises that what is so peculiar about a unit circle and what is its importance in mathematics that we need to learn about it separately inline any other circle having a different centre and a radius. Let us find out.

Importance of Unit Circle in Mathematics

The unit circle plays a significant role in a number of different areas of mathematics. Some of the areas where we find extensive use and application of unit circles include:

1. The functions of trigonometry are most simply defined using the unit circle.
2. The unit circle has the ability to explicitly write the coordinates of a number of points lying on the unit circle with very little computation.
3. The unit circle can also be considered to be the contour in the complex plane defined by |x| = 1, where |x| represents the complex modulus
4.  The unit circle is considered as the so-called ideal boundary of the two-dimensional hyperbolic plane H² in both the Poincaré hyperbolic disk and Klein-Beltrami models of hyperbolic geometry.

Let us now study the use of unit circles in trigonometry.

Trigonometric Functions using Unit Circle

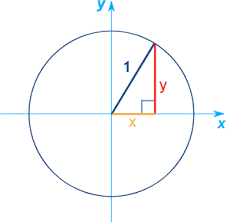
The trigonometric functions of sine, cosine, and tangent can be calculated using a unit circle. In order to calculate the trigonometric functions, we will first need to apply the Pythagoras theorem in a unit circle. Therefore, let us consider a right triangle placed in a unit circle in the Cartesian coordinate plane. In this plane,

• The hypotenuse of the right triangle is represented by the radius of the circle.
• An angle θ with the positive x-axis is made by the radius vector.
• The coordinates of the endpoint of the radius vector are (x, y)
• The length of the base is the value of x while the length of the altitude is the value of y

Therefore, for any angle t, we can label the intersection of its side and the unit circle by its coordinates, ( x, y ). The coordinates x and y will be the outputs of the trigonometric functions f(t)=cost and f(t)=sin t respectively. This means:

x = cos t

y = sin t

The following diagram shows these coordinates:

This can also be verified by using the Pythagoras theorem, as stated above. Using Pythagoras theorem, we will get:

sin θ = $\frac{Altitude}{Hypotenuse}=\frac{x}{1}=x$

cos θ = $\frac{Base}{Hypotenuse}=\frac{y}{1}=y$

Now that we have obtained the value of sin θ and cos θ, we can find out the value of tan θ

tan θ = $\frac{\sin \theta }{\cos\theta}$

Similarly, we find the values of other trigonometric functions.

Let us understand this through an example.

Suppose, we have the below d that shows the point $(\frac{-\sqrt{2}}{2}, \frac{\sqrt{2}}{2})$ with coordinates on a unit circle.

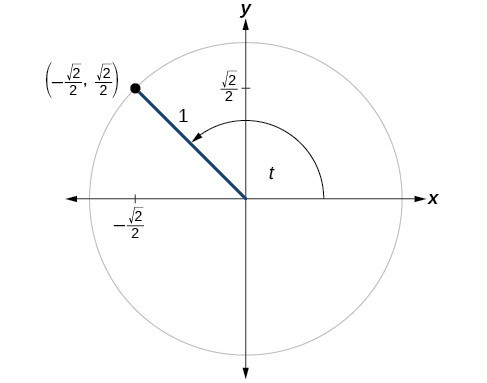
We have already learnt the x-coordinate of any unit circle is equal to sin t while the y-coordinate of the unit circle is equal to cost t. This means that

x = $\frac{-\sqrt{2}}{2}$,

y  = $\frac{\sqrt{2}}{2}$

Therefore,

tan t = $\frac{\sin t}{\cos t}$

Unit Circle Chart in Radians

To understand the unit circle in radians, we first need to understand what we mean by radians. Radians are another way of measuring angles, and the measure of an angle can be converted between degrees and radians. Some key points regarding radians are:

• One radian is the measure of the central angle of a circle such that the length of the arc is equal to the radius of the circle.
• One complete circle which measures 360^o is equal to 2π radians. This implies that 1 radian =$\frac{180^{\circ }}{\pi }$
• The formula used to convert between radians and degrees is defined by:

Angle in degrees = Angle in radians x $\frac{180^{\circ }}{\pi }$

• If s is the length of an arc of a circle, and r is the radius of the circle, then the measure of the radian is given by the central angle that contains that arc.

Radians vs Degrees

The difference between the degrees and the radians can be described as –

Degree	Radian
Degrees, denoted by °, are a measurement of angle size that is determined by dividing a circle into 360 equal pieces.	Radians are unitless but are always written with respect to π. They measure an angle in relation to a section of the unit circle’s circumference.

In trigonometry, most calculations use radians. Therefore, it is important to know how to convert between degrees and radians using the following conversion factors.  Therefore, now that we have understood that the complete range of a circle can be represented by either 360 degrees or 2π radians, we can relate radians and degrees in the following manner:

2π radians = 360^o

1 radian  = $\frac{360^{\circ }}{2\pi }$

1 radian  = $\frac{180^{\circ }}{\pi }$

The following figure shows the relation between the radians and the degrees at various points on the circle.

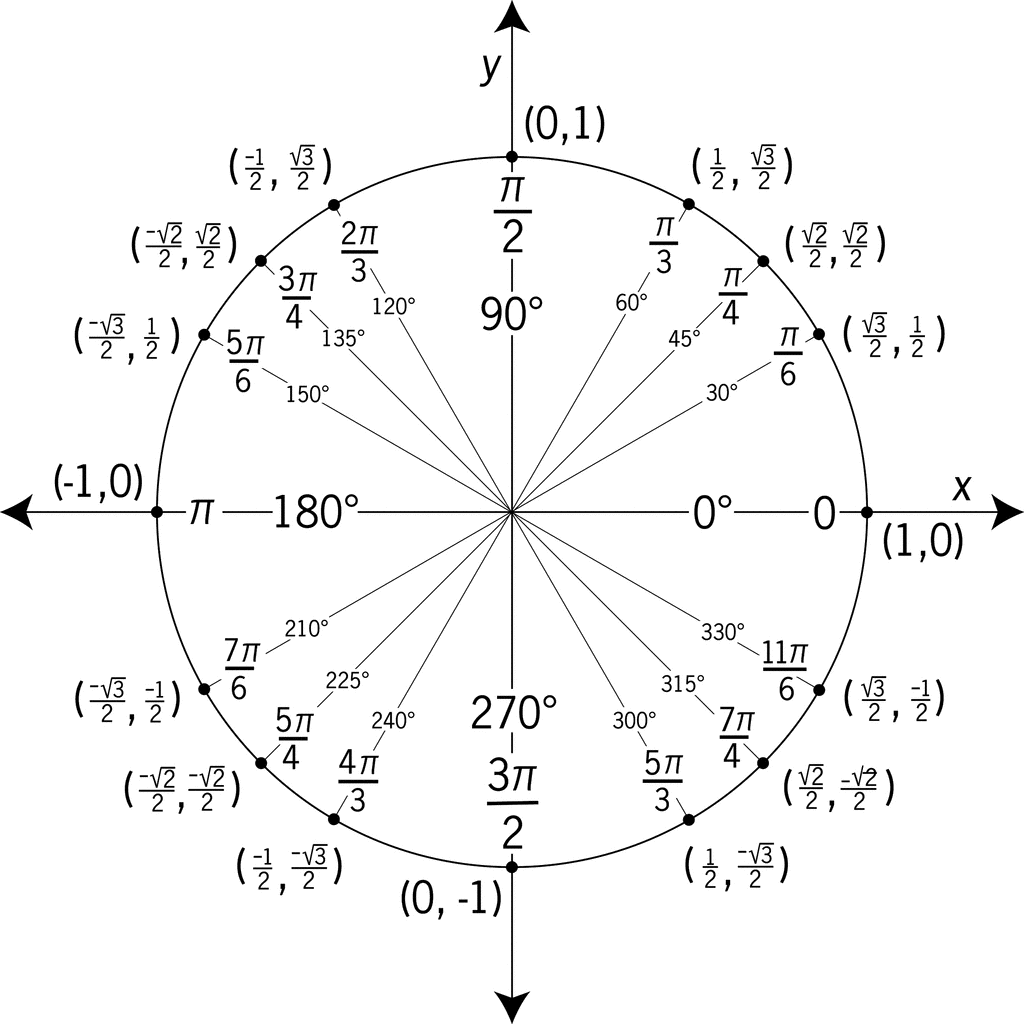
In the figure, above, the circle is marked and labelled in both radians and degrees at all quadrant angles and angles that have reference angles of 30°, 45°, and 60°. At each angle, the coordinates are given. These coordinates can be used to find the six trigonometric values/ratios. The x-coordinate is the value of cosine at the given angle and the y-coordinate is the value of sine. It is important to remember that the unit circle demonstrates the periodicity of trigonometric functions by showing that they result in a repeated set of values at regular intervals. By periodicity here, we mean the quality of a function with a repeated set of values at regular intervals.

Let us understand this through an example.

Example

Convert an angle measuring $\frac{\pi}{9}$ radians to degrees.

Solution

In order to convert the given radians into degrees, we will use the relation between the radians and the degrees that we have defined above. We know that:

Angle in degrees = Angle in radians x $\frac{180^{\circ }}{\pi }$

So, Angle in degrees =  $\frac{\pi}{9}\times \frac{180^{\circ }}{\pi }$  = 20^o

 Hence, $\frac{\pi}{9}$ radians = 20^o

The relation between the radians and the degrees can also be presented through the following chart.

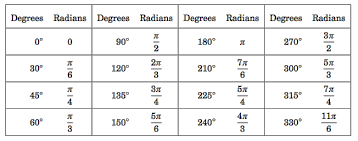
Unit Circle Table

The following chart describes different values of the trigonometric functions both in radians as well as in degrees.

Quadrant System in Trigonometry

It is important to note that the sign of a trigonometric function is dependent on the signs of the coordinates of the points on the terminal side of the angle. So, we know the quadrant in which the terminal side of an angle lies, we can also get to know the signs of all the trigonometric functions. So, how do we determine the sign of the trigonometric function? Let us find out.

We know that the distance from a point to the origin is always positive. However, the signs of the x and y coordinates may be positive or negative, depending upon their position on the unit circle. The entire unit circle is divided into four quadrants as described in the below diagram:

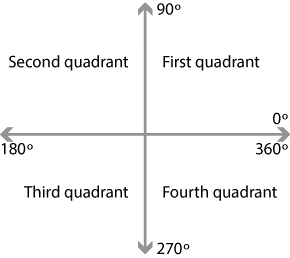
Now, let us take the case of each quadrant one by one.

First Quadrant – In the first quadrant, we can see that both the x and the y coordinates are all positive. This means that all the six trigonometric functions will have positive values in the first quadrant.

Second Quadrant – In the second quadrant, only sine and cosecant (the reciprocal of sine) are positive while all the remaining trigonometric functions will have negative values.

Third Quadrant – In the third quadrant, only tangent and cotangent are positive while all the remaining trigonometric functions will have negative values.

Fourth Quadrant – In the fourth quadrant, only cosine and secant are positive while all the remaining trigonometric functions will have negative values.

The following is the representation of the trigonometric functions in the four quadrants.

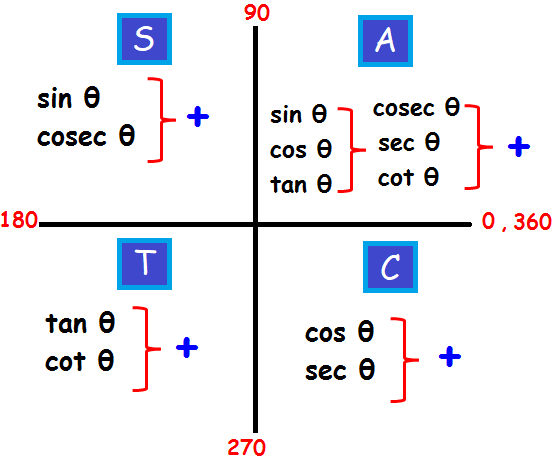
How to remember these signs?

The sign on a trigonometric function depends on the quadrant that the angle falls in, and the mnemonic phrase “A Smart Trigo Class” is used to identify which functions are positive in which quadrant, where

A – All positive in First Quadrant

Smart – Sine positive in second quadrant

Trigo – Tan positive in the third quadrant

Class – Cos positive in the fourth quadrant.

Solved Examples

Example 1    

What point corresponds to the angle −π on the unit circle?

Solution              

We are required to find the point that corresponds to the angle −π on the unit circle.

Now, we know that the unit circle is the circle of radius one that has its centre at the origin (0,0) in the Cartesian coordinate system. 

We also know that −π is equivalent to −180^o which corresponds to the point ( −1, 0 ) on the unit circle.

Hence, the point that corresponds to the angle −π on the unit circle is (-1, 0 )

Example 2    

If we consider a unit circle on a Cartesian coordinate plane, then what will be the coordinates for an angle of $\frac{\pi}{4}$?

Solution              

We have been given the angle $\frac{\pi}{4}$. We need to find the coordinates of this angle on the Cartesian coordinate plane.

Now, we know that The coordinates of the point on the circle for each angle are ( cosθ, sinθ ).

We also know that,

 $cos\frac{\pi}=\frac{\sqrt{2}}{2}$ and $sin\frac{\pi}=\frac{\sqrt{2}}{2}$

Therefore, the point will be $(\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2})$.

Hence, the coordinates for an angle of $\frac{\pi}{4}$ will be $(\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2})$.

Example 3    

Convert 120° to radians.

Solution              

We know that the relationship between degrees and the radians is given by:

Angle in degrees = Angle in radians x $\frac{180^{\circ }}{\pi }$

Therefore,

120 = Angle in radians x $\frac{180^{\circ }}{\pi }$

Hence,

Angle in radian = $\frac{120\times \pi}{180}=\frac{2\pi}{3}$

Therefore, 120° will be equal to $\frac{2\pi}{3}$ radians.

Remember

• The equation of a unit circle is x² + y²  =1
• The radius of the unit circle is always one unit.
• The centre of the unit circle is the point of origin, i.e. ( 0, 0 ).
• One radian is the measure of the central angle of a circle such that the length of the arc is equal to the radius of the circle.
• One complete circle which measures 360^o is equal to 2π radians. This implies that 1 radian = $\frac{180^{\circ }}{\pi }$
• The formula used to convert between radians and degrees is defined by:

Angle in degrees = Angle in radians x $\frac{180^{\circ }}{\pi }$

• The standard unit is used to measure angles in mathematics. The measure of a central angle of a circle that intercepts an arc equal in length to the radius of that circle.
• The x and y coordinates at a point on the unit circle given by an angle t are defined by the functions x=cos t and y=sin t.
• The unit circle demonstrates the periodicity of trigonometric functions by showing that they result in a repeated set of values at regular intervals.
• Periodicity means the quality of a function with a repeated set of values at regular intervals.
• The sign on a trigonometric function depends on the quadrant that the angle falls in, and the mnemonic phrase “A Smart Trigo Class” is used to identify which functions are positive in which quadrant.

Recommended Worksheets

Circumference of a Circle (Summer Party Themed) Worksheets
Area of a Circle (Home Decorations & Furniture Themed) Worksheets
Understanding Circumference and Area of a Circle 7th Grade Math Worksheets