Rectangular Prism

Introduction

In geometry, a three-dimensional shape can be defined as a solid figure or an object or shape that has three dimensions – length, width and height. 3 Dimensional shapes or 3D shapes are the shapes that have all the three dimensions, i.e. length, breadth and height.  This means that unlike two-dimensional shapes, three-dimensional shapes have thickness or depth. In other words, they are solid objects and these objects have fixed shapes and sizes. In our everyday lives, we come across many solid shapes. For example, the laptop, our rooms, mobile phones, ice cream, tennis balls, etc. are all examples of solid shapes. 

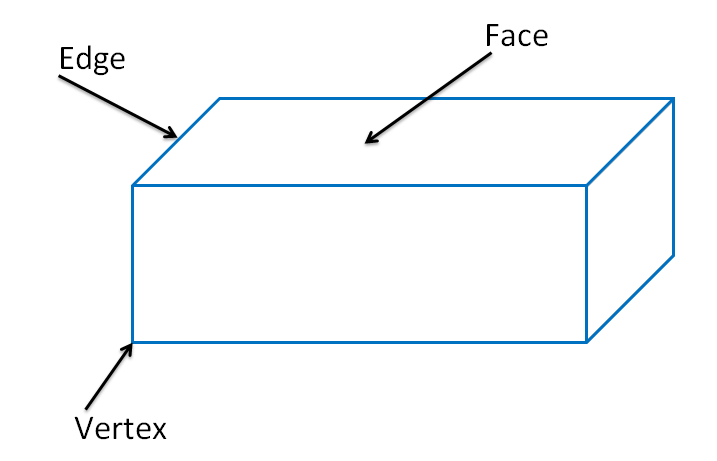
It is important to understand here that any 3 dimensional shape has three integral attributes. These attributes are faces, vertices and edges. The following figure gives an idea of a 3 dimensional shape and its attributes.

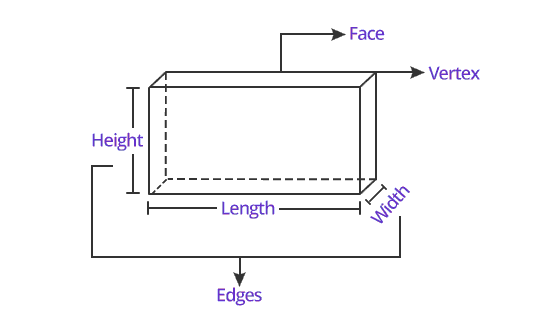
One of such 3 dimensional shapes is a polyhedron. So, what is a polyhedron? Let us find out.

Polyhedron

A solid shape bounded by polygons is called a polyhedron. The word polyhedra are the plural of the word polyhedron. If the line segment joining any two points on the surface of a polyhedron entirely lies inside or out the polyhedron then it is called a convex polyhedron. One such type of polyhedron is a rectangular prism? What is it and what are its properties? Let us find out?

Definition

A rectangular prism is a polyhedron with two congruent and parallel bases. Some of the real-life examples of a rectangular prism are rooms, notebooks, geometry box etc. Following is the general representation of a rectangular prism. 

Let us now discuss about the faces, vertices and edges of a rectangular prism. Before, that let us recall what we mean by faces, vertices and edges.

Faces – Polygons forming a polyhedron are known as its faces. In other words, a face refers to any single flat surface of a 3D shape. For example, observe one side of your room or that of a Rubik’s cube. Every side has two dimensions, be it a length and a breadth, or a breadth and a height or a length and a height. Each side of a room forms its face. 

How many faces does a rectangular prism have? It has 6 faces.  

Edges – Line segments common to intersecting faces of a polyhedron are known as its edges. In other words, an edge is a line segment on the boundary joining one vertex (corner point) to another.    It is similar to the sides we have in 2D shapes.  

How many edges does a rectangular prism have? It has 12 vertices  

Vertices – Points of intersection of edges of a polyhedron are known as its vertices. In other words, the meeting point of a pair of sides of a polygon is called its vertex.

How many vertices does a rectangular prism have? It has 8 vertices  

The following figure shows the representation of faces, vertices and edges in a rectangular prism?

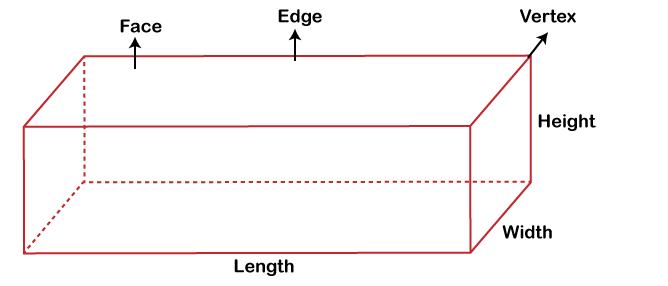
Let us now learn about the properties of a rectangular prism.

Properties

The properties of a rectangular prism are – 

1. A rectangular prism has 6 faces, 12 edges and 8 vertices
2. The top and base of the rectangular prism are always a rectangle.
3. Pairs of opposite faces are identical or congruent.
4. It has a rectangular cross-section.

Net of a Rectangular Prism

What is the net of a polyhedron? We know that the net of any geometrical figure is obtained when it is unfolded along its edges and its faces are laid out in a pattern in two dimensions. By this definition, the net of a polyhedron is like an unfolded cardboard construction of that polyhedron. So, how will the net of a rectangular prism look like? The following is the net obtained when we open a rectangular prism along its surfaces. We can see that the nets of rectangular prisms are made up of rectangular and square shapes.

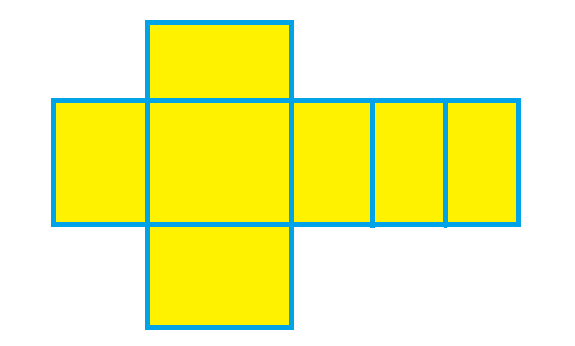
Types of Rectangular Prisms

There are two types of rectangular prisms – 

1. Oblique Rectangular Prism
2. Right Rectangular Prism

Let us discuss about them one by one.

Oblique Rectangular Prism

An oblique rectangular prism is a prism in which all the angles are not right angles. This means that a rectangular prism is a prism in which bases are not perpendicular to each other which is why it is called the oblique rectangular prism. In simple words, in an oblique rectangular prism, bases that are not aligned one directly above the other. Following is the general representation of an oblique rectangular prism. 

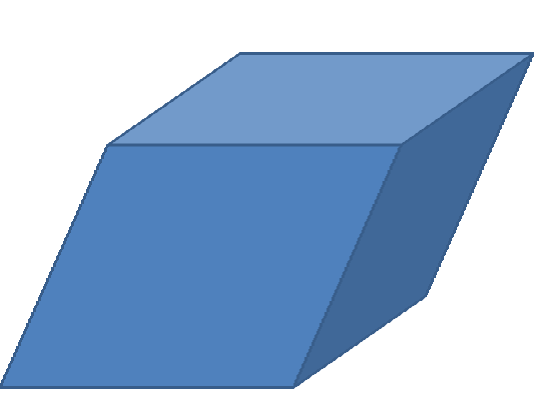
Right Rectangular Prism

A prism with rectangular bases is called a rectangular prism. In other words, a rectangular prism in which bases are perpendicular to each other is called the right rectangular prism. Following is the general representation of a right rectangular prism. 

Is Rectangular Prism a Cuboid?

Is cuboid and rectangular prism the same? Let us find out. We already know what a rectangular prism is. Let us recall the definition of a cuboid.

We know that a 3D shape having six rectangular faces is called a cuboid, for example, a matchbox, a brick, a book etc. In other words, it is an extension of a rectangle in a 3D plane. Other examples of cuboids include almirah, room, playing board box etc. a cuboid has length, breadth and height. Various parts of a cuboid are – 

Faces

A cuboid has 6 rectangular faces. The opposite faces of a cuboid are identical. 

Edges

Two adjacent faces of a cuboid meet in a line segment called an edge of the cuboid. A cuboid has 12 edges.

Vertex

Three edges of a cuboid meet at a point called a vertex. A cuboid has 8 vertices

From above we can see that there are strong similarities between the shape and properties of a cuboid and a rectangular prism. Hence, we can say that due to its shape, a rectangular prism is also called a cuboid.

Volume of a Rectangular Prism

We should recall that the space occupied by a three-dimensional object is called the volume of that object. So, what will be the volume of a rectangular prism? Let us find out.

The volume of a rectangular prism is the amount of space covered by a rectangular prism. In other words, the number of units used to fill a rectangular prism is called the volume of a rectangular prism. The unit of volume is the cubic unit or unit³. This means that that the volume of any prism is obtained by multiplying its base area by its height. So, we have,

Using the formula for the area of a rectangle, we can find the base area of a rectangular prism. This means that –

The base area of the rectangular prism =  length of the rectangular prism x breadth of the rectangular prism.

Now, let the length of the rectangular prism = l and

Breadth of the rectangular prism = b

Also, the height of the rectangular prism = h

Then,

The volume of the rectangular prism = base area of the rectangular prism x height

Therefore,

Volume of a rectangular prism = l x b x h

For example, we have a rectangular prism where the length of its base is 6 cm; the width of the base is 5 cm while its height is 4 cm. The volume would then be given by – 

Volume (V) = l x w x h

Where

l = 6cm, w = 5cm and h = 4cm

Volume = 6 x 5 x 4 = 120 cu. cm

Not the units of the volume. The volume of any geometrical figure is always given in cubic units.

Surface Area of a Rectangular Prism

The surface area of a rectangular prism is the measure of how much exposed area a prism has. When we talk of surface areas of a rectangular prism, there are two types of surface areas of a rectangular prism – 

1. Lateral surface area (LSA)
2. Total surface area (TSA) 

Let us understand both of them one by one.

Lateral Surface Area of a Rectangular Prism

The lateral surface area of a rectangular prism is the sum of the surface area of all its faces without the base of the rectangular prism. The lateral surface area of any right rectangular prism is equivalent to the perimeter of the base times the height of the prism. This means that –

Lateral surface area of a rectangular prism = Perimeter of the Base x Height ………….. ( 1 )

Now, the perimeter of the base is given by two times the sum of the length and the breadth. Therefore, we can say that

The Perimeter of the base =  2 ( l + b ) where

length of the rectangular prism = l and

Breadth of the rectangular prism = b

If the height of the rectangular prism = h and we substitute all the above values in the equation ( 1), we get,

Lateral surface area of a rectangular prism = = 2 ( l + b ) x h

Total Surface Area of a Rectangular Prism

The total surface area of a rectangular prism is the sum of the areas of all of its faces. So, how do we calculate the total surface area of a rectangular prism?

The total surface area of a rectangular prism is the sum of the lateral surface area (LSA) and twice the base area of the rectangular prism. This means that – 

Total surface area of a rectangular prism = Lateral Surface Area + 2 x Area of the Base

Therefore, 

Total surface area of a rectangular prism = 2 ( l + b ) x h + 2 x Area of the Base

Now, area of the base = length x breadth  = l x b

So, 

Total surface area of a rectangular prism = 2 ( l + b ) x h + 2 x ( l x b )

⇒ Total surface area of a rectangular prism = 2 l h + 2 b h + 2 l b

⇒ Total surface area of a rectangular prism = 2 ( l h + b h + l b )

Hence, 

 Total surface area of a rectangular prism = 2 ( l h + b h + l b )

Examples

Example 1 Find the surface area of a rectangular prism whose length, width, and height are 8cm, 6cm, and 4cm, respectively.

Solution We have been given that the length, width, and height are 8cm, 6cm, and 4cm, respectively. We need to find the surface area of the rectangular prism. Now, we know that – 

Total surface area of a rectangular prism = 2 ( l h + b h + l b )  ……….. ( 1 )

Now, we have

Length = l = 8 cm

Breadth = b = 6 cm

Height = h = 4 cm

Now, substituting all the above values in the equation ( 1), we get,

Total surface area of a rectangular prism = 2 ( 8 × 4 + 6 × 4 + 8 × 6)

⇒ Total surface area of a rectangular prism = 2 ( 32 + 24 + 48 )

⇒ Total surface area of a rectangular prism = 2 x 104 sq. cm

⇒ Total surface area of a rectangular prism = 208 sq. cm

Hence, Total surface area of a rectangular prism = 208 sq. cm

Example 2 Calculate the volume of the following rectangular box.

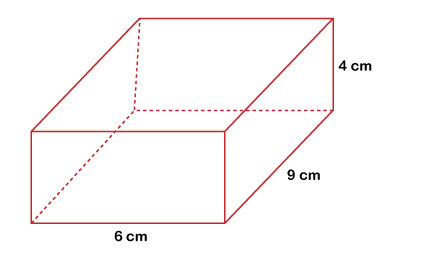
Solution We have been given a rectangular box and we need to find its volume. It can be clearly seen that the shape of the rectangular box resembles that of a rectangular prism. So, we will use the formula for calculating the volume of a rectangular prism. 

Now, we know that 

Volume of a rectangular prism = l x b x h where, ………………………. ( 1 )

length of the rectangular prism = l

Breadth of the rectangular prism = b and

height of the rectangular prism = h

Now, we have been given that 

length of the rectangular prism = l = 9 cm

Breadth of the rectangular prism = b = 6 cm

height of the rectangular prism = h = 4 cm

Now, substituting all the above values in the equation ( 1), we get,

Volume of a rectangular prism = 9 x 6 x 4 cu. cm

⇒  Volume of a rectangular prism = 216 cu. cm

Hence, the volume of the given rectangular box = 216 cu. cm

Example 3 A gift is packed in a rectangular box (rectangular prism) of dimensions 15 cm, 10 cm, and 8 cm and it needs to be wrapped with gift paper. How much gift paper is required to wrap the gift box?

Solution We have been given that a gift is packed in a rectangular box (rectangular prism) of dimensions 15 in, 10 in, and 8 in and it needs to be wrapped with gift paper. We need to find how much gift paper is required to wrap the gift box. It has been given that the rectangular box is in the shape of a rectangular prism. Let us first summarise the information that has been given to us.

Length of the rectangular box = 15 cm

Breadth of the rectangular box = 10 cm

Height of the rectangular box = 8 cm

Now, to find the amount of gift paper required, we need to find the total surface area of the box. Since, it has been given that the rectangular box is in the shape of a rectangular prism, therefore, we will use the formula of finding the total surface area of a rectangular prism to find how much gift paper is required to wrap the gift box. Therefore, we have

Total Surface Area of a rectangular prism = 2 ( l w + w h + h l )

= 2 [(15 × 10) + (10 × 8) + (8 × 15)]

= 2 (150 + 80 + 120)

= 700 sq. cm 

Hence, the amount of gift paper is required to wrap the gift box = 700 sq. cm

Key Facts and Summary

1. 3 Dimensional shapes or 3D shapes are the shapes that have all the three dimensions, i.e. length, breadth and height.  
2. A solid shape bounded by polygons is called a polyhedron.
3. A rectangular prism is a polyhedron with two congruent and parallel bases.
4. A rectangular prism has twelve edges, six faces, and eight vertices.
5. The net of a polyhedron is like an unfolded cardboard construction of that polyhedron.
6. An oblique rectangular prism is a prism in which all the angles are not right angles.
7. A prism with rectangular bases is called a rectangular prism.
8. A rectangular prism is also called a cuboid.
9. The volume of a rectangular prism is the amount of space covered by a rectangular prism.
10. The volume of the rectangular prism = base area of the rectangular prism x height
11. The lateral surface area of a rectangular prism is the sum of the surface area of all its faces without the base of the rectangular prism.
12. Lateral surface area of a rectangular prism = Perimeter of the Base x Height
13. The total surface area of a rectangular prism is the sum of the areas of all of its faces.
14. Total surface area of a rectangular prism = 2 ( l h + b h + l b )