Trigonometry

What is Trigonometry?

Trigonometry is an important branch of mathematics that is used to study the relationship between ratios of the sides of a right-angled triangle with its angles. The word “trigonometry” is derived from the Greek words, “trigon” and “metron”. The word “trigon” means a triangle and the word ”metron” means a measure. Hence, trigonometry means the science of measuring triangles. In broader cases it is that branch of mathematics which deals with the measurement of the sides and the angles of a triangle and the problems allied with the angles.

Though the field emerged in Greece during the third century B.C., some of the most important contributions (such as the sine function) came from India in the fifth century A.D. Because early trigonometric works of Ancient Greece have been lost, it is not known whether Indian scholars developed trigonometry independently or after Greek influence. According to Victor Katz in “A History of Mathematics (3rd Edition)” (Pearson, 2008), trigonometry developed primarily from the needs of Greek and Indian astronomers.

Before moving on to understand the concepts in trigonometry, it is important to recall what we mean by an angle.

An angle is considered as the figure obtained by rotating a given ray about its end point. The measure of an angle is the amount of rotation from the initial side to the terminal side.

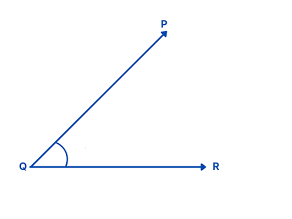
In the above figure, QR is the initial side and PQ is the terminal side.

Now let us learn about trigonometric ratios.

What are Trigonometric Ratios?

Consider an acute angle ∠YAX = θ with initial side AX and terminal side AY. Let P be any point on the terminal side AY. Draw PM perpendicular from P on AX to get the right angled triangle AMP in which ∠PAM = θ.

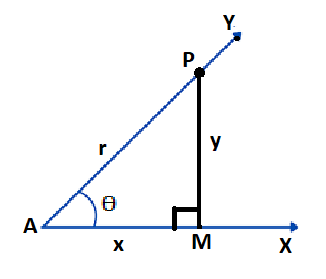
Now, in the right angled triangle AMP, Base = AM = x and Perpendicular = PM = y and Hypotenuse = AP = r

We define the following six trigonometric ratios

Sin θ = $\frac{Perpendiculur}{Hypotenuse}=\frac{y}{r}$, written as sin θ
Cos θ = $\frac{Base}{Hypotenuse}=\frac{x}{r}$, written as cos θ
Tan θ = $\frac{Perpendiculur}{Base}=\frac{y}{x}$, written as tan θ
Cosecant θ = $\frac{Hypotenuse}{Perpendicular}=\frac{r}{y}$, written as cosec θ
Secant θ = $\frac{Hypotenuse}{Base}=\frac{r}{x}$, written as sec θ
Cotangent θ = $\frac{Base}{Perpendicular}=\frac{x}{y}$, written as cot θ

It is important to note here that by sin θ we mean “sine of angle θ” and not the product of sin and θ. Similar is the case for other trigonometric ratios.

Does the value of trigonometric ratios change with change of points on the angle? Let us find out.

The above trigonometric ratios, as we can see depend upon the value of angle θ and are independent of the position of the point P on the terminal side AY of the acute angle ∠XAY. This means that if we choose P somewhere else on AY, then the lengths PM, AM and AP will change. However, the trigonometric ratios will remain same. Hence we can say that –

The trigonometric ratios are same for the same angle.

Relation between Trigonometric Ratios

The trigonometric ratios sin θ, cos θ and tan θ of an angle θ are very closely connected by a relation. If any one of them is known, the other two can be easily calculated. Let us see how.

Let us again consider the following figure –

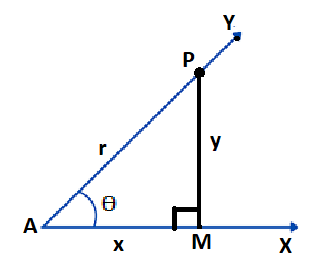
We have learnt above that

Sin θ = $\frac{PM}{AP}$

There are only three values that constitute all the angles Base, Perpendicular and the Hypotenuse. Hence, if we know the value of one of the angles, this means we know two of these three values using which we can find the remaining value. Suppose, if we know the value of sin θ, we can easily calculate the value of the base using the Pythagoras theorem. We have,

PM² + AM² = AP²

Now, since we have the value of sin θ, we know the value of the perpendicular and the hypotenuse using which we will get the value of the base.

Therefore, it is clear from the definitions of the trigonometric ratios that for any acute angles θ, we have,

cosec θ = $\frac{1}{sinsinθ}$
sec θ = $\frac{1}{coscosθ}$
cot θ = $\frac{1}{tantanθ}$
cot θ = $\frac{coscosθ}{sinsinθ}$
tan θ = $\frac{sinsinθ}{coscosθ}$
tan θ. Cot θ = 1

Let us understand this with an example.

Example If sin A = $\frac{3}{5}$, find the value of cos A and tan A

Solution We have been given that sin A = $\frac{3}{5}$

We have also learnt that sin θ = $\frac{Perpendiculur}{Hypotenuse}$

This means that $\frac{Perpendiculur}{Hypotenuse}= \frac{3}{5}$

So, we draw a triangle ABC, right angled at B such that Perpendicular = BC = 3 units and Hypotenuse = Ac = 5 units.

By Pythagoras theorem we have,

AC² = AB² + BC²

5² = AB² + 3²

AB² = 5² – 3²

AB² = 25 – 9

AB² = 16

⇒ AB = 4

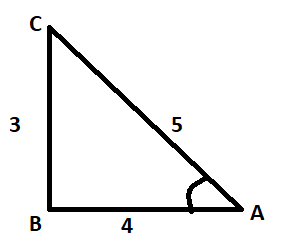
Now, that we know the value of AB, we can find the value of cos A

cos A = $\frac{Base}{Hypotenuse}=\frac{4}{5}$

Also, tan A = $\frac{Perpendiculur}{Base}=\frac{3}{4}$

Trigonometric Ratios of Some Specific Angles

Now, we shall learn about the trigonometric ratios of some standards angles which have been derived using some elementary knowledge of geometry.

Trigonometric Ratios of 0^o and 90^o

Let XAY = θ be an acute angle and let P be a point on its terminal side AY. Draw a perpendicular PM from P to AX.

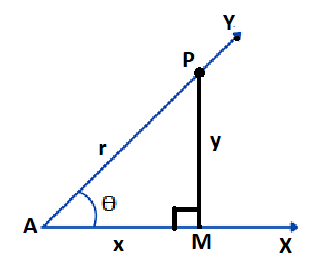
In Δ AMP, we have,

sin θ = $\frac{PM}{AP}$

cos θ = $\frac{AM}{AP}$

tan θ = $\frac{PM}{AM}$

It is evident from Δ AMP that as θ becomes smaller and smaller line segment Pm also becomes smaller and smaller and finally when θ becomes 0^o, the point P will coincide with M. Consequently, we have,

PM = 0 and AP = AM

Therefore,

sin 0⁰ = $\frac{PM}{AP}=\frac{0}{AP}$ = 0

Similarly,

cos 0⁰ = $\frac{AM}{AP}=\frac{AP}{AP}$ = 1

and

tan 0⁰ = $\frac{PM}{AM}=\frac{0}{AM}$ = 0

Thus, we have,

sin 0⁰ = 0, cos 0⁰ = 1 and tan 0⁰ = 0

Similarly, cosec 0⁰ = Not defined sec 0⁰ = 1 and cot 0⁰ = Not Defined

From Δ AMP, it is evident that as θ increases, the lien segment AM becomes smaller and smaller and finally when θ becomes 90^o, the point M will coincide with A. Consequently, we have,

AM = 0, AP = PM

Therefore,

sin 90⁰ = $\frac{PM}{AP}=\frac{PM}{PM}$ = 1

Similarly,

cos 90⁰ = $\frac{AM}{AP}=\frac{0}{AP}$ = 0

and

tan 90⁰ = $\frac{PM}{AM}=\frac{PM}{0}$ = Not Defined

Thus, we have,

sin 90⁰ = 1, cos 90⁰ = 0 and tan 0⁰ = Not Defined

Similarly, cosec 90⁰ = 1sec 90⁰ = Not Defined, cot 90⁰ = 0

Trigonometric Ratios of 30^o and 60^o

Consider an equilateral triangle ABC with each side of length 2a. Since each angle of an equilateral triangle is 60^o, therefore, each angle of the triangle ABC will be equal to 60^o. Let AD be perpendicular from A on BC. Since the triangle is equilateral, therefore, AD is the bisector of angle A and D is the mid-point of BC.

Therefore,

BD = DC = a and ∠BAD = 30^o

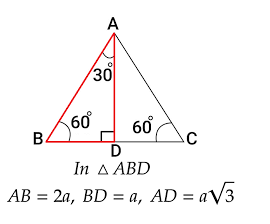
Thus in triangle ABD, ∠D is a right angle, hypotenuse AB = 2a and BD = a

So, by Pythagoras theorem, we have

AB² = AD² + BD²

⇒ (2a)² = AD² +a²

⇒ AD² = 4a² – a²

⇒ AD = $\sqrt{3}$a

Trigonometric Ratios of 30^o

So, now we have,

Base = AD = $\sqrt{3}$a, Perpendicular = BD = a, Hypotenuse = AB = 2a and ∠DAB = 30^o

Therefore,

sin 30⁰ = $\frac{BD}{AB}=\frac{a}{2a} =\frac{1}{2}$

Similarly,

cos 30⁰ = $\frac{AD}{AB}=\frac{\sqrt{3a}}{2a}=\frac{\sqrt{3}}{2}$

and

tan 30⁰ = $\frac{BD}{AD}=\frac{a}{\sqrt{3a}}=\frac{1}{\sqrt{3}}$

Thus, we have,

sin 30⁰ = $\frac{1}{2}$, cos 30⁰ = $\frac{\sqrt{3}}{2}$ and tan 30⁰ = $\frac{1}{\sqrt{3}}$

Similarly, cosec 30⁰ = 2, sec 30⁰ = $\frac{2}{\sqrt{3}}$ and cot 30⁰ = $\sqrt{3}$

Trigonometric Ratios of 60^o

In right triangle ADB, we have,

Base = BD = a, Perpendicular = AD = $\sqrt{3}$a, Hypotenuse = AB = 2a and ∠DAB = 60^o

sin 60⁰ = $\frac{AD}{AB}=\frac{\sqrt{3a}}{2a}=\frac{\sqrt{3}}{2}$

cos 60⁰ = $\frac{BD}{AB}=\frac{a}{2a}=\frac{1}{2}$

tan 60⁰ = $\frac{AD}{AB}=\frac{\sqrt{3a}}{a}=\sqrt{3}$

Thus, we have,

sin 60⁰ =$\frac{\sqrt{3}}{2}$ , cos 60⁰ = $\frac{1}{2}$, and tan 60⁰ =$\sqrt{3}$

Similarly, cosec 60⁰ = $\frac{2}{\sqrt{3}}$ , sec 60⁰ = 2 and cot 60⁰ = $\frac{1}{\sqrt{3}}$

Trigonometric Ratios of 45^o

Consider a right angled triangle ABC with right angle at B such that ∠A = 45^o. Then,

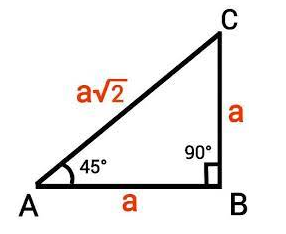
Therefore, we have,

∠A + ∠B +∠C = 180^o

⇒ 45^o + 90^o + ∠C = 180^o

⇒ ∠C = 45^o

Hence, we can say that ∠A = ∠C

This means that AB = BC

Let AB = BC = a. then by Pythagoras theorem, we have,

AC² = AB² + BC²

⇒ AC² = a² + a²

⇒ AC² = 2a²

⇒ AC = $\sqrt{2}$a

Therefore, we have

sin 45⁰ = $\frac{BC}{AC}=\frac{a}{\sqrt{2a}}=\frac{1}{\sqrt{2}}$

Similarly,

cos 45⁰ = $\frac{AB}{AC}=\frac{a}{\sqrt{2a}}=\frac{1}{\sqrt{2}}$

and

tan 45⁰ = $\frac{BC}{AB}=\frac{a}{a}$= 1

Thus, we have,

sin 45⁰ = $\frac{1}{\sqrt{2}}$ , cos45⁰ = $\frac{1}{\sqrt{2}}$ and tan 45⁰ = 1

Similarly, cosec 45⁰ = $\sqrt{2}$, sec 45⁰ = $\sqrt{2}$, and cot 45⁰ = 1

The following table gives us the values of various trigonometric ratios of 0^o, 30^o, 45^o, 60^o and 90^o for ready reference.

Angles/T. Ratios	0^o	30^o	45^o	60^o	90^o
sin θ	0	$\frac{1}{2}$	$\frac{1}{\sqrt{2}}$	$\frac{\sqrt{3}}{2}$	1
cos ͔͔θ	1	$\frac{\sqrt{3}}{2}$	$\frac{1}{\sqrt{2}}$	$\frac{1}{2}$	0
tan θ	0	$\frac{1}{\sqrt{3}}$	1	$\sqrt{3}$	Not Defined
cosec θ	Not Defined	2	$\sqrt{2}$	$\frac{2}{\sqrt{3}}$	1
sec θ	1	$\frac{2}{\sqrt{3}}$	$\sqrt{2}$	2	Not Defined
cot θ	Not Defined	$\sqrt{3}$	1	$\frac{1}{\sqrt{3}}$	0

Let us understand their use through an example.

Example 1 Evaluate the value of sin60^ocos30^o + cos60^osin30^o

Solution We have,

sin60^ocos30^o + cos60^osin30^o

From the above table, we can obtain the values of the given trigonometric ratios. So, we get –

sin60^o = $\frac{\sqrt{3}}{2}$

cos30^o = $\frac{\sqrt{3}}{2}$

cos60^o = $\frac{1}{2}$

sin30^o = $\frac{1}{2}$

Replacing these values in the given express we have,

sin60^ocos30^o + cos60^osin30^o

= $\frac{\sqrt{3}}{2}$ x $\frac{\sqrt{3}}{2}$ + $\frac{1}{2}$ x $\frac{1}{2}$

= $\frac{3}{4}$ + $\frac{1}{4}$ = 1

Hence, sin60^ocos30^o + cos60^osin30^o = 1

Trigonometric Ratios of Complementary Angles

Now that we have learnt the values of the trigonometric ratios on various degrees, we shall obtain the trigonometric ratios of complementary angles in terms of the trigonometric ratios of the given angles.

Let us recall what we mean by complementary angles. Two angles are said to be complementary if their sum is 90^o. It follows from this definition that θ and ( 90^o – θ ) are complementary angles for an acute angles θ.

So, we have

sin ( 90^o – θ ) = cos θ

cos ( 90^o – θ ) = sin θ

tan ( 90^o – θ ) = cot θ

cot ( 90^o – θ ) = tan θ

sec ( 90^o – θ ) = cosec θ

cosec ( 90^o – θ ) = sec θ

Let us understand these formulae with an example

Example Find the value of $\frac{coscos 37^{0}}{sinsin 53^{0}}$

Solution We have,

$\frac{coscos 37^{0}}{sinsin 53^{0}}$

= $\frac{coscos 90^{0} – 53^{0}}{sinsin 53^{0}}$

= $\frac{sinsin 53^{0}}{sinsin 53^{0}}$ = 1

Hence, $\frac{coscos 37^{0}}{sinsin 53^{0}}$ = 1

Solved Examples

Example 1 If cosec θ = √10, then find the values of all T-ratios of θ.

Solution we have been given that cosec θ = √10. We are required to find the value of the remaining five trigonometric ratios.

Now, we have learnt that

cosecant θ = $\frac{Hypotenuse}{Perpendicular}$

Since, we have

cosec θ = √10, therefore,

$\frac{Hypotenuse}{Perpendicular} = \frac{\sqrt{10}}{1}$

So, we draw a right triangle ABC, right angled at B such that,

Perpendicular = BC = 1 unit and

Hypotenuse = AC = $\sqrt{10}$ units

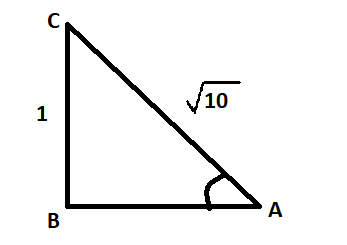
Now, using the Pythagoras theorem we have,

AC² = AB² + BC²

⇒ (√10 )² = AB² + 1

⇒ AB² = 10 – 1 = 9

⇒ AB = 3

When we consider the trigonometric ratios of A, we have,

Base = AB = 3 units, Perpendicular = BC = 1 unit and Hypotenuse = AC = $\sqrt{10}$ units

So,

sin θ = $\frac{Perpendiculur}{Hypotenuse}=\frac{1}{\sqrt{10}}$

cos θ = $\frac{Base}{Hypotenuse}=\frac{3}{\sqrt{10}}$

tan θ = $\frac{Perpendiculur}{Base}=\frac{1}{3}$

sect θ = $\frac{Hypotenuse}{Base}=\frac{\sqrt{10}}{3}$

cot θ = $\frac{Base}{Hypotenuse}=\frac{3}{1}$ = 3

Example 2 cot 12° cot 38° cot 52° cot 60° cot 78°

Solution We are required to find the value of cot12°cot38°cot52°cot60°cot78°

In order to find the value of the given expression, we shall first group the terms in such a way that the angles involved are complementary i.e. their sum is 90^o, we have,

= ( cot 12° cot 78° ) (cot 38° cot 52° ) cot 60°

= (cot 12° tan 12° ) (cot 38° tan 38° ) cot 60°

Now, we know that

cot 78° = cot ( 90 – 12 )^o = tan 12°

Also,

cot 52° = cot ( 90 – 52 )^o = tan 38°

Therefore, the given expression can be written as

= (cot 12° tan 12° ) (cot 38° tan 38° ) cot 60°

= 1 x 1 x $\frac{1}{\sqrt{3}}$ = $\frac{1}{\sqrt{3}}$

Hence, cot 12° cot 38° cot 52° cot 60° cot 78° = $\frac{1}{\sqrt{3}}$

Example 3 Evaluate the following expression

2 sin² 30^o tan 60^o – 3 cos² 60^o sec² 30^o

Solution We are required to find the value of the expression

2 sin² 30^o tan 60^o – 3 cos² 60^o sec² 30^o

In order to find this value, we will first need to recall the values of the given trigonometric ratios in the expression

We have learnt that

sin 30^o = $\frac{1}{2}$

tan 60^o = $\sqrt{3}$

cos 60^o = $\frac{1}{2}$

sec 30^o = $\frac{2}{\sqrt{3}}$

Substituting the above values in the given expression we have,

2 sin² 30^o tan 60^o – 3 cos² 60^o sec² 30^o

= 2 x ($\frac{1}{2}$)² x $\sqrt{3}$ – 3 x ($\frac{1}{2}$) ² x ($\frac{2}{\sqrt{3}}$) ²

= 2 x $\frac{1}{4}$ x $\sqrt{3}$ – 3 x $\frac{1}{4}$ x $\frac{4}{3}$

= $\frac{\sqrt{3}}{2}$ – 1 = $\frac{\sqrt{3}-2}{2}$

Hence, the value of the given expression 2 sin² 30^o tan 60^o – 3 cos² 60^o sec² 30^o is $\frac{\sqrt{3}-2}{2}$

Remember

Trigonometry means the science of measuring triangles.
The trigonometric ratios are the same for the same angle.
Sin θ = $\frac{Perpendiculur}{Hypotenuse}=\frac{y}{r}$, written as sin θ
Cos θ = $\frac{Base}{Hypotenuse}=\frac{x}{r}$, written as cos θ
Tan θ = $\frac{Perpendiculur}{Base}=\frac{y}{x}$, written as tan θ
Cosecant θ = $\frac{Hypotenuse}{Perpendicular}=\frac{r}{y}$, written as cosec θ
Secant θ = $\frac{Hypotenuse}{Base}=\frac{r}{x}$, written as sec θ
Cotangent θ = $\frac{Base}{Perpendicular}=\frac{x}{y}$, written as cot θ
cosec θ = $\frac{1}{sinsinθ}$
sec θ = $\frac{1}{coscosθ}$
cot θ = $\frac{1}{tantanθ}$
cot θ = $\frac{coscosθ}{sinsinθ}$
tan θ = $\frac{sinsinθ}{coscosθ}$
tan θ. Cot θ = 1
sin ( 90^o – θ ) = cos θ
cos ( 90^o – θ ) = sin θ
tan ( 90^o – θ ) = cot θ
cot ( 90^o – θ ) = tan θ
sec ( 90^o – θ ) = cosec θ
cosec ( 90^o – θ ) = sec θ
sin 0⁰ = 0, cos 0⁰ = 1 and tan 0⁰ = 0
cosec 0⁰ = Not defined sec 0⁰ = 1 and cot 0⁰ = Not Defined
sin 30⁰ = $\frac{1}{2}$, cos 30⁰ = $\frac{\sqrt{3}}{2}$ and tan 30⁰ = $\frac{1}{\sqrt{3}}$
cosec 30⁰ = 2, sec 30⁰ = $\frac{2}{\sqrt{3}}$ and cot 30⁰ = $\sqrt{3}$
sin 45⁰ = $\frac{1}{\sqrt{2}}$, cos45⁰ = $\frac{1}{\sqrt{2}}$ and tan 45⁰ = 1
cosec 45⁰ = $\sqrt{2}$, sec 45⁰ = $\sqrt{2}$, and cot 45⁰ = 1
sin 60⁰ =$\frac{\sqrt{3}}{2}$ , cos 60⁰ = $\frac{1}{2}$, and tan 60⁰ =$\sqrt{3}$
cosec 60⁰ = $\frac{2}{\sqrt{3}}$, sec 60⁰ = 2 and cot 60⁰ = $\frac{1}{\sqrt{3}}$
sin 90⁰ = 1, cos 90⁰ = 0 and tan 0⁰ = Not Defined
cosec 90⁰ = 1sec 90⁰ = Not Defined and cot 90⁰ = 0

Recommended Worksheets

Trigonometric Identities
Sohcahtoa
Circumference of a Circle (Summer Party Themed) Worksheets

Browse All Worksheets

We spend a lot of time researching and compiling the information on this site. If you find this useful in your research, please use the tool below to properly link to or reference Helping with Math as the source. We appreciate your support!