Introduction
The square of the number became interesting to people when they collided with the area, that is more than two millennia ago. Initially, people calculated areas using practical methods, and later invented formal methods – formulas. To get the area of the square, ancient people used stones. They placed stones in equal numbers of rows and columns and counted the total number of stones.
To date, there are many convenient and easy ways (both algebraic and geometric) to calculate the squares of numbers. Here we will tell you all the most interesting facts about perfect square numbers.
Triangular and square numbers
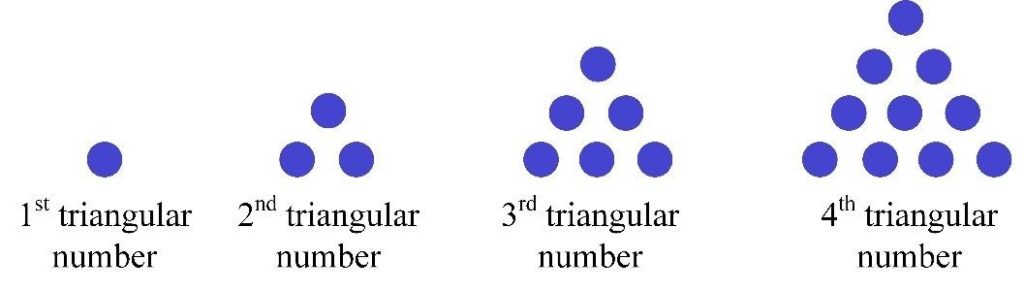
Represent each natural number as corresponding number of dots.

As you can see that dots for some numbers can be arranged in triangles and dots for other numbers can be arranged in squares. Those numbers which dots’ representations are triangles are called triangular numbers and numbers which dots’ representations are squares are called square numbers. So, the diagram above shows that
- four first triangular numbers are 1, 3, 6, 10;
- three first square numbers are 1, 4, 9.
PROPERTY OF TRIANGULAR NUMBERS: nth triangular number is the sum of n consecutive natural numbers from 1 to n.
To demonstrate this property, turn the triangular numbers a little differently. Thus, you can see that each row of dots contains one more dot than the previous row.
So,
1st triangular number 1 is the sum of only one natural number 1;
2nd triangular number 3 is the sum of two consecutive natural numbers 1 and 2;
3rd triangular number 6 is the sum of three consecutive natural numbers 1, 2 and 3;
4th triangular number 10 is the sum of four consecutive natural numbers 1, 2, 3 and 4;
…
nth triangular number is the sum of n consecutive natural numbers 1, 2, …, n-1 and n.
Moreover, we can prove that nth triangular number equals to $\frac{n(n+1)}{2}$. Since n consecutive natural numbers 1, 2, …, n-1 and n form an arithmetic sequence, then the sum of these numbers is
$\frac{First\: number\:+\:Last\: number}{2}$⋅Number of numbers=$\frac{1+n}{2}$⋅n
that is $\frac{n(n+1)}{2}$.
Not impressed? Then take a look at the rectangle below. It has width of 7 dots and length of 8 dots.

Draw the line as shown in the diagram and notice that this line divides the rectangle into two congruent triangles representing two 7th triangular numbers 28. But 28=$\frac{1}{2}$56=$\frac{1}{2}$(7×8). So, the 7th triangular number has so many dots as half of rectangle 7 by 8 has.
In the same way, constructing a rectangle n by n+1 dots, we obtain that hth triangular number consists of half of the total number of dots in this rectangle. There are n(n+1) dots in the rectangle n by n+1 dots, so hth triangular number consists of $\frac{1}{2}$n(n+1) dots.
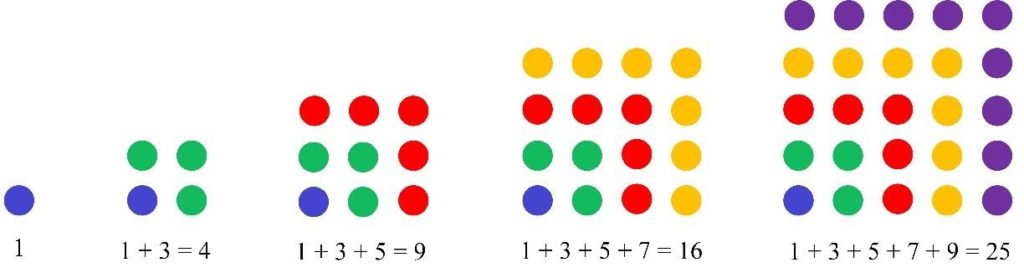
PROPERTY OF SQUARE NUMBERS: nth square number is the sum of the first n consecutive odd natural numbers from 1 to 2n-1.
First, demonstrate this property graphically for small square numbers.
1st square number is natural number 1;
2nd square number 4 is the sum of the first two odd numbers 1 and 3;
3rd square number 9 is the sum of the first three odd numbers 1, 3 and 5;
4th square number 16 is the sum of the first four odd numbers 1, 3, 5 and 7;
…
nth square number n2 is the sum of the first n odd numbers 1, 3, … , 2n-1.
It is easy to check that nth square number n2 is the sum of the first n odd numbers 1, 3, … , 2n-1. Since numbers 1, 3, … , 2n-1 form an arithmetic sequence, its sum is
$\frac{1+2n-1}{2}⋅n = \frac{2n}{2}$⋅n=n⋅n=n2
If you rearrange dots from the diagram above as follows, you can see these sums of odd numbers clearer.

There are some relationships between triangular and square numbers.
FACT 1: Twice the nth triangular number added to the number n+1 gives a square number (n+1)2.
First, illustrate it for small triangular and square numbers.
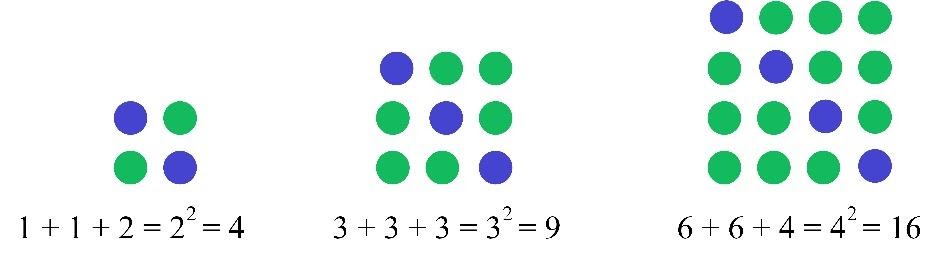
Now, prove this fact for all triangular numbers. The nth triangular number equals to $\frac{n(n+1)}{2}$. Twice the nth triangular number added to the number n+1 is
2$\frac{n(n+1)}{2}+(n+1)=n(n+1)+(n+1)=(n+1)(n+1)=(n+1)^2$
FACT 2: When we add the nth triangular number to the (n+1)th triangular number, the sum is always a square number (n+1)2.
First, illustrate it for small triangular and square numbers.
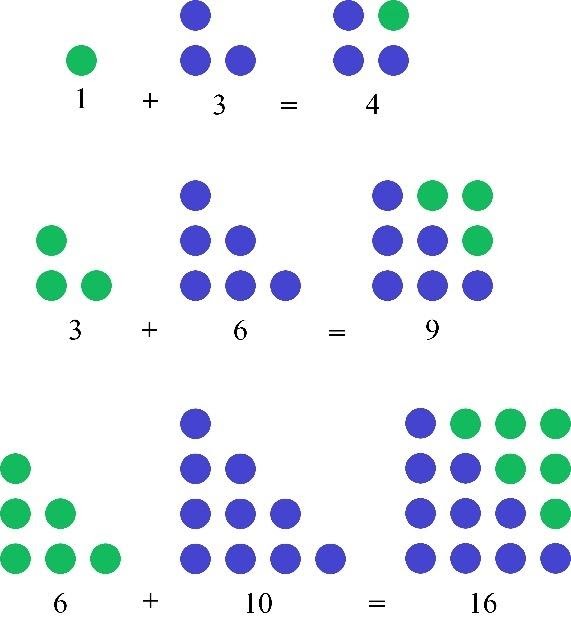
Now, prove this fact for all triangular numbers. The nth triangular number equals to $\frac{n(n+1)}{2}$, the (n+1)th triangular number is $\frac{(n+1)((n+1)+1)}{2}=\frac{(n+1)(n+2)}{2}$. Thus, the sum of these numbers is
$\frac{n(n+1)}{2}+\frac{(n+1)(n+2)}{2}=\frac{(n+1)(n+n+2)}{2}=\frac{(n+1)(2n+2)}{2}=\frac{(n+1)(2)(n+1)}{2}=$
=(n+1)(n+1)=(n+1)2
What are perfect square numbers?
A perfect square number or square number is a natural number that is the square of an integer. In other words, it is the product of some integer with itself. For example, 4 is a square number, since it equals 22. Number 4 can also be represented as (-2)2. But since we are talking about square numbers, and they are always positive, for convenience we will consider only the squares of natural numbers, remembering that the squares of corresponding negative numbers will be the same.
If number N is a perfect square number, then there exists such natural number n, that
N=n2
List of square numbers
If you often work with numbers, square numbers up to 30 are easily recognizable. If you do not work with numbers often, or you need larger square numbers, you can use the following table.
Table of perfect squares
(the numbers in the table are squares of the column number plus row number)
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 0 | 1 | 4 | 9 | 16 | 25 | 36 | 49 | 64 | 81 | 100 |
| 10 | 121 | 144 | 169 | 196 | 225 | 256 | 289 | 324 | 361 | 400 |
| 20 | 441 | 484 | 529 | 576 | 625 | 676 | 729 | 784 | 841 | 900 |
| 30 | 961 | 1024 | 1089 | 1156 | 1225 | 1296 | 1369 | 1444 | 1521 | 1600 |
| 40 | 1681 | 1764 | 1849 | 1936 | 2025 | 2116 | 2209 | 2304 | 2401 | 2500 |
| 50 | 2601 | 2704 | 2809 | 2916 | 3025 | 3136 | 3249 | 3364 | 3481 | 3600 |
| 60 | 3721 | 3844 | 3969 | 4096 | 4225 | 4356 | 4489 | 4624 | 4761 | 4900 |
| 70 | 5041 | 5184 | 5329 | 5476 | 5625 | 5776 | 5929 | 6084 | 6241 | 6400 |
| 80 | 6561 | 6724 | 6889 | 7056 | 7225 | 7396 | 7569 | 7744 | 7921 | 8100 |
| 90 | 8281 | 8464 | 8649 | 8836 | 9025 | 9216 | 9409 | 9604 | 9801 | 10000 |
For example, what is the square of 57? Represent number 57 as 50+7, find 50 in the first column and 7 in the first row. Row corresponding to number 50 and column corresponding to number 7 intersect at number 3249. So, 57th square number or simply 572 is 3249.
Using this table, you can also check whether given number is a square number or not. For example,
- number 6724 is a square number as it is in the table. Number 6724 stands at the intersection of row corresponding to number 80 and column corresponding to number 2, so 6724=822;
- number 3529 is not a square number (it is absent in the table).
The table shows that the gaps between two neighbor square numbers each time increase more and more. Indeed, if we recall that the nth square number is the sum of n consecutive odd numbers, then
- nth square number is the sum 1+3+5+…+(2n-1);
- (n+1)th square number is the sum 1+3+5+…+2n-1+2n+1;
- the difference between (n+1)th square number and nth square number is an odd number 2n+1.
You can prove this property easier, using formula for the difference of two squares,
(n+1)2-n2=(n+1-n)(n+1+n)=(1)(2n+1)=2n+1
although the first method seems much more elegant to the author.
How to identify square numbers?
There are some properties of perfect squares which can be used to test whether a number is a perfect square or not. They can definitely say if a given number is not a square number.
PROPERTY 1: If a number ends with 2, 3, 7 or 8, then this number is not a perfect square number.
Carefully studying the table of square numbers, you can see that all the square numbers end with the digits 0, 1, 4, 5, 6, 9.
How can we prove this fact? There are ten digits, 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9. Square these digits:
02=0
12=1
22=4
32=9
42=16
52=25
62=36
72=49
82=64
92=81
These squares end with digits 0, 1, 4, 5, 6, 9. Since unit digit of a square of any number is the unit digit of the square of its last digit, all square numbers end only with digits 0, 1, 4, 5, 6, 9 too.
PROPERTY 2: If a square number ends with some number of 0, then it ends with even number of zeros.
PROPERTY 3: If a square number ends with 5, then it ends with number 25.
PROPERTY 4: A number can be a perfect square if its digital root is 1, 4, 7, or 9.
Let us remind what is a digital root of a number – a digital root of a number is the single digit obtained when all digits of a number are added together. If a sum is not a single digit, then add the digits of the sum and so on until we get the single digit.
For example, to find the digital root of 4496 add all digit of this number
4+4+9+6=33
33 is not a one-digit number, so add its digits too
3+3=6
Now, we get a single digit 6. This means the digital root of number 4496 is 6. Since number 6 is not in the list of possible digital roots for square numbers, number 4496 is not a perfect square number.
These four properties of square numbers help us to sieve non-perfect squares. So,
- if a number ends with 2, 3, 7 or 8, it is not a perfect square number;
- if a number ends with odd number of zeros, then it is not a perfect square number;
- if a number ends with 5, but the ten’s digit is not 2, then it is not a perfect square number;
- if a digital root is 0, 2, 3, 5, 6 or 8, then it is not a perfect square number.
If you assume that a number may be a square number, then this can be verified by factoring this number. If in the prime factorization of the number only even powers of prime factors are present, then given number is a perfect square number, else – it is not.
EXAMPLE: Check whether each number is a perfect square number.
a) 104976;
b) 23384.
SOLUTION: a) Find the prime factorization of the given number:
104976=2×52488=2×2×26244=2×2×2×13122=2×2×2×2×6561
=2×2×2×2×3×2187=2×2×2×2×3×3×729
=2×2×2×2×3×3×3×243 =2×2×2×2×3×3×3×3×81
=24 x 34 x 34=24 x 38
So, number 104976=(22 x 34)2=3242 is a perfect square number.
b) Find the prime factorization of the given number:
23384=2×11692=2×2×5846=2×2×2×2923
=2×2×2×37×79=23×37×79
Since the prime factorization of number 23384 doesn’t consists only of even powers of prime numbers, then given number is not a perfect quare number.
Additional properties of square numbers
Some properties we have discussed in the previous topic. But there are still many interesting properties of square numbers.
PROPERTY 5: The square of even numbers is always even, and the square of odd numbers is always odd.
PROPERTY 6: Square numbers always have an odd number of factors. One pair of factors always consists of two identical factors.
PROPERTY 7: A perfect square always leaves remainder 0 or 1 when divided by 3.
All natural numbers are of the form 3k, 3k+1 or 3k+2.
- if a natural number n=3k, then the square n2=(3k)2=9k2 leaves the remainder 0 when divided by 3;
- if a natural number n=3k+1, then the square n2=(3k+1)2=9k2+6k+1 leaves the remainder 1 when divided by 3;
- if a natural number n=3k+2, then the square n2=(3k+2)2=9k2+6k+4 also leaves the remainder 1 when divided by 3.
PROPERTY 8: A perfect square always leaves remainder 0 or 1 when divided by 4.
- if a natural number n is an even number, then it can be represented as n=2k and the square of this number is (2k)2=4k2. Number 4k2 always leaves the remainder 0 when divided by 4;
- if a natural number n is an odd number, then it can be represented as n=2k+1 and the square of this number is (2k+1)2=4k2+4k2+1. Number 4k2+4k+1 always leaves the remainder 1 when divided by 4.
PROPERTY 8: A perfect square always leaves the remainder 0, 1, 4 or 9 when divided by 12.
Readers can try to prove this property on their own.
Special cases for two-digit numbers
There are certain rules that help quickly square numbers. These rules apply to all two-digit numbers.
CASE 1: If a number ends with zeros, then square the number without zeros and add twice as many zeros as in the original number.
For example, to square number 80, square 8 and then add two zeros. The result is 6400.
CASE 2: If a number ends with 5, multiply the ten’s digit of the number by a digit that is 1 greater than ten’s digit is and write 25 at the end.
For example, to find 352, multiply 3 by 3+1=4 and write 25 at the end, so the result is 1225.
CASE 3: Rule for numbers from 40 to 50:
ab × ab =1500+100×b+10-b2
For example, 482=1500+100×8+(10-8)2=1500+800+4=2304
(Here, the ten’s digit doesn’t matter, it is always 4 as numbers are from 40 to 50)
CASE 4: Rule for numbers from 50 to 60:
ab × ab =2500+100×b+b2
For example, 532=2500+100×3+32=2500+300+9=2809
(Here, the ten’s digit doesn’t matter, it is always 5 as numbers are from 50 to 60)
CASE 5: Rule for numbers from 90 to 100:
ab × ab =8000+200×b+(10-b)2
For example, 962=8000+200×6+(10-6)2=8000+1200+16=9216
(Here, the ten’s digit doesn’t matter, it is always 9 as numbers are from 90 to 100)
CASE 6: Just learn squares from 10 to 25. It is easy as they are very common.
CASE 7: Rule for numbers from 25 to 40:
ab×ab=100(ab-25)+(50-ab)2
For example, 342=100(34-25)+(50-34)2=100(9)+162=900+256=1156
There are two more additional universal cases.
CASE 8: Rule for numbers from 50 to 100:
ab×ab=200(ab-50)+(100-ab)2
For example, 732=200(73-50)+(100-73)2=200(23)+272=4600+729=5329
CASE 9: For any two-digit number you can use the square of the sum formula:
(ab)2=(10a+b)2=100a2+20ab+b2
For example, 842=(80+4)2=802+2⋅80⋅4+42=6400+640+16=7056
Quiz
- Which statement is true? Explain your reasoning.
a) Each triangular number is an odd number.
b) Each square number is an even number.
c) The sum of two consecutive square numbers is a triangular number.
d) The sum of two consecutive triangular numbers is a square number.
SOLUTION: a) This statement is false. For example, triangular number 6 is an even number.
b) This statement is false. For example, square number 25 is an odd number.
c) This statement is false. For example, number 13 which is the sum of two square numbers 4 and 9, is not a triangular number.
d) This statement is true; it was proven in this article.
- Why each of the following numbers is not a perfect square number?
156705, 389000, 6689037, 740981, 90674
SOLUTION: 1) Number 156705 ends with 5. To be a perfect square number, number ending with 5 must end with 25. Since our number ends with 05, it is not a perfect square number.
2) Number 389000 ends with three zeros. To be a perfect square number, number must end with even number of zeros, so number 389000 is not a perfect square number.
3) Number 6689037 ends with 7. If the unit digit in a number is 2, 3, 7 or 8, this number couldn’t be a perfect square number. Therefore, number 6689037 is not a perfect square number.
4) Number 740981 ends with 1, so it could happen that it is a perfect square number. Find the digital root for this number:
7+4+0+9+8+1=29
2+9=11
1+1=2
If the digital root differs from digits 1, 4, 7 or 9, then the corresponding number is not a perfect square number.
5) Number 90674 ends with 4, so it could happen that it is a perfect square number. But when we divide number 90674 by 4, the remainder is 2. All perfect square numbers leave the remainder 0 or 1 when divided by 4. Thus, number 90674 is not a perfect square number.
- Using described algorithms of squaring numbers, square the following two-digit numbers.
a) 36;
b) 49;
c) 83.
SOLUTION: a) Number 36 is from 25 to 50, so
362=100(36-25)+(50-36)2=100(11)+142=1100+196=1296
b) Number 49 is from 40 to 50, so
492 =1500+100×9+(10-9)2=1500+900+1=2401
c) Number 83 is from 50 to 100, so
832=200(83-50)+(100-83)2=200(33)+172=6600+289=6889
ANSWER: a) 1296 b) 2401 c) 6889
- Which of the following numbers is a square number? Explain why.
a) 11025;
b) 32571.
SOLUTION: a) Find the prime factorization of the given number:
11025=5×2205=5×5×441=5×5×3×147=5×5×3×3×49
=5×5×3×3×7×7=32 x 52 x 72
So, number 11025=(3×5×7)2=1052 is a perfect square number.
b) Find the prime factorization of the given number:
32571=3×10857=3×3×3619=3×3×7×517
=3×3×7×11×47=32×7×11×47
Since the prime factorization of number 32571 doesn’t consists only of even powers of prime numbers, then given number is not a perfect square number.
ANSWER: a) square number b) not square number
- Find all natural numbers n for which n+200 is a perfect square number.
SOLUTION: The smallest perfect square number greater than 200 is 225, so the smallest possible value of n is 225-200=25.
The next perfect square number greater than 225 is 256, so the next possible value of n is 256-200=56.
The difference between 56 and 25 is 31. This means that the next difference between two consecutive values of n will be 31+2=33, and so on. To see this pattern, fill in the following table.
| n+200 | n | Difference | |
| 225 | 25 | ||
| 256 | 56 | 56-25 | 31 |
| 289 | 89 | 89-56 | 33 |
| 324 | 124 | 124-89 | 35 |
| 361 | 161 | 161-124 | 37 |
| 400 | 200 | 200-161 | 39 |
| 441 | 241 | 241-200 | 41 |
If you want to write general rule describing all possible values of n, this can be done using following recurrent formulas:
n1=25,
nk=nk-1+(2k+27), k= 2, 3, 4, …
ANSWER: nk=nk-1+(2k+27), where k=2, 3, 4, … and n1=25
Conclusions
- Each triangular number is the sum of consecutive natural numbers.
- Each square number is the sum of consecutive odd natural numbers.
- If number N is a perfect square number, then there exists such natural number n, that N=n2.
- Twice the nth triangular number added to the number n+1 gives a square number (n+1)2.
- When we add the nth triangular number to the (n+1)th triangular number, the sum is always a square number (n+1)2.
- Many properties of square numbers help us to determine whether a given number is perfect square number or not.
- People have discovered a lot of patterns that make our lives easier, in particular, when squaring a number, we can use a lot of tricks.
Recommended Worksheets
Measuring Area Using Square Grids (Painting Themed) Worksheets
Counting 2-3 Digit Numbers (International Children’s Book Day Themed) Math Worksheets
Even and Odd Numbers (Ages 6-8) Worksheets (Labor Day Themed)









