Lateral Surface Area of a Cone

Introduction

The study of geometry, specifically the study of shapes and their properties, forms a cornerstone of mathematics. One such concept that often comes up in theoretical and practical applications is the lateral surface area of a cone. This article will explore each aspect of this mathematical idea, which can be seen, measured, and used in real-world situations.

Grade Appropriateness

The concept of the lateral surface area of a cone is typically introduced in middle school and becomes a staple in high school geometry. This concept is appropriate for students in grades 8 through 12, depending on the depth and complexity of the course. It is also revisited in college-level math courses, especially calculus and advanced geometry.

Math Domain

This topic falls under Geometry, a branch of mathematics that deals with questions of size, shape, space properties, and figures’ relative position.

Applicable Common Core Standards

This topic aligns with the following Common Core Standards:

CCSS.MATH.CONTENT.7.G.B.4: Know the formulas for the area and circumference of a circle and use them to solve problems.

CCSS.MATH.CONTENT.HSG.GMD.A.1: Give an informal argument for the formulas for the circumference of a circle, the circle’s area, the volume of a cylinder, a pyramid, and a cone.

Definition of the Topic

The lateral surface area of a cone refers to the area of the outer surface, excluding the base. It is the surface area you would need to paint or wrap around a cone. In mathematical terms, it is calculated as πrl, where l refers to the slant height and r refers to the radius of the base of the cone.

Key Concepts

Cone: A three-dimensional geometric figure that tapers from a flat base to the tip or vertex.

Radius (r): The measure from the centre of the base of the cone to its edge.

Slant Height (l): The distance from the apex of the cone, down the side, to the edge of the base.

Lateral Surface Area: The curved surface area of the cone, excluding the base.

Discussion with Illustrative Examples

The term “lateral” suggests an object’s side. Add all of an object’s surfaces, except its base(s), to determine its lateral surface area. 

With cones, the lateral surface area is defined as the area of its curved surface. Therefore, the lateral surface area of cones can also be called a curved surface area.

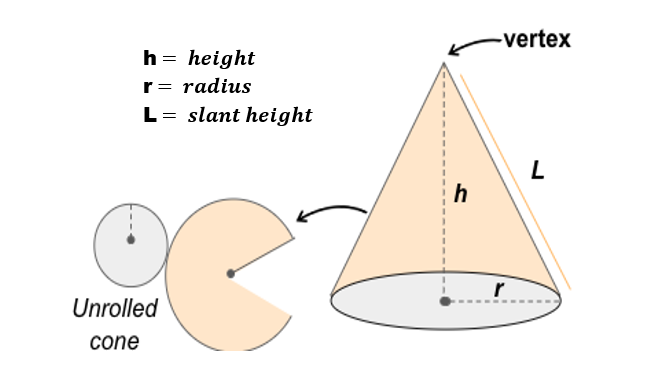
A three-dimensional shape like the cone has a circular base and a curved surface which narrows towards a point called the vertex.

To solve for the lateral surface area, we need to multiply the radius (r) by the slant height (L) multiplied by pi (π).

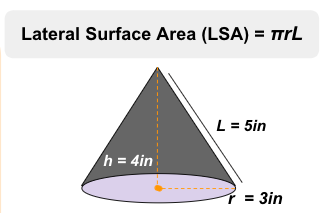
Follow these steps to find the Lateral Surface Area (LSA) of a cone:

Look for and identify the value of radius (r).

Identify the slant height (L) of the cone’s curved surface.

Multiply the radius (r) and slant height (L) by pi (π).

Label your final answer in square units.

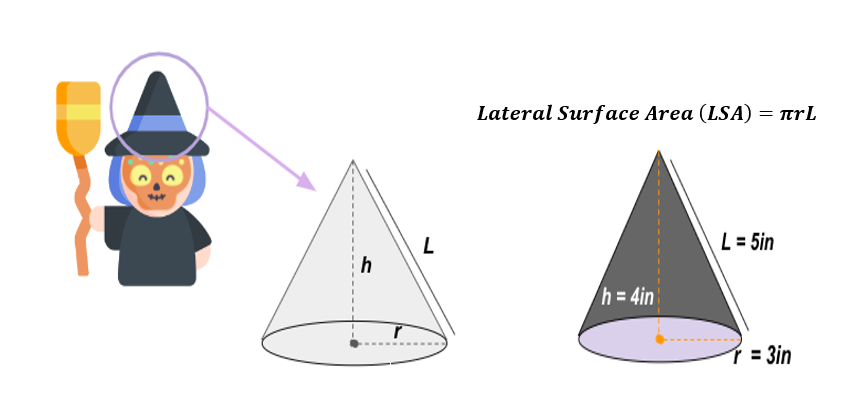
Let’s solve the hat’s LSA with the abovementioned dimensions, assuming that π (pi) is 3.14.

Lateral surface area: 

LSA = πrL

LSA = (3.14)(3 in)(5 in)

LSA = 47.1in²

The lateral surface area of the Calaveras hat is 47.1 in².

What if the slant height(L) is not provided? 

In finding the slant height (L), there is a need to go back to the Pythagorean Theorem. A slant height is a distance along the curved surface from the vertex to the base of either a pyramid or cone. Therefore, a slant height is the shortest possible distance from a vertex to a base.

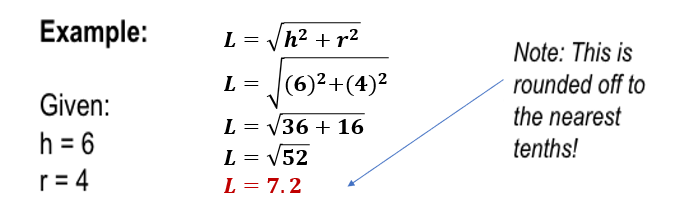
Examples with Solution

Example 1

Solve for the lateral surface area of the cone.

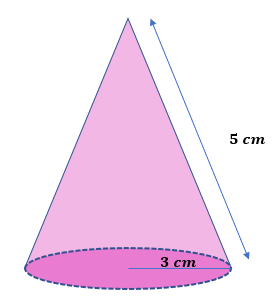
Solution

Lateral Surface Area = πrl = (π)(3 cm)(5 cm) = 15π cm².

Example 2

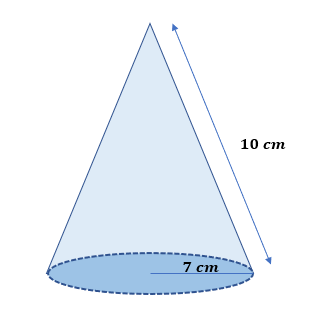
Find the cone’s lateral surface area with a radius of 7 cm and slant height of 10 cm.

Solution

Lateral Surface Area = πrl = (π)(7 cm)(10 cm) = 70π cm².

Example 3

Solve the lateral surface area of the cone below.

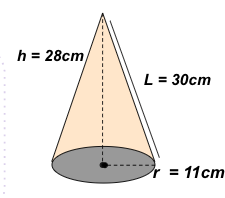
Solution

LSA= πrL

LSA = (3.14) (11cm) (30cm)

LSA = 1036.2 cm²

Therefore, the lateral surface area of this cone  is 1036.2cm²

Example 4

Compute the lateral surface area:

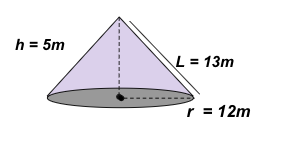
Solution

LSA= πrL

LSA = (3.14) (12m) (13m)

LSA = 489.84 m²

Therefore, the lateral surface area of this cone is 489.84 m².

Example 5

Find the measure of the slant height and compute the lateral surface area:

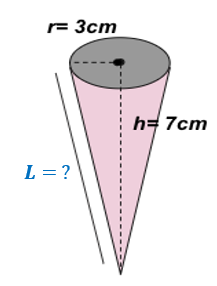
Solution

For the slant height, we have,

L=$\sqrt{h^2+r^2}$

L=$\sqrt{(7 cm)^2+(3 cm)^2}$

L=$\sqrt{49 cm^2+9 cm^2}$

L=$\sqrt{58 cm^2}$

L=7.6 cm (Rounded off to the nearest tenths)

For the lateral surface area of the cone,

LSA= πrL

LSA = (3.14) (3 cm) (7.6 cm)

LSA = 71.592 cm²

Therefore, the lateral surface area of this cone is 71.592 cm².

Real-life Application with Solution

Suppose you plan to make a cone-shaped party hat from a piece of cardboard. The hat’s slant height is 15 cm, with a 5 cm radius for the base. How much cardboard will you require to make the hat?

Solution

The amount of cardboard needed corresponds to the lateral surface area of the cone. 

Using our formula, we get the following:

Lateral Surface Area = πrl = (π)(5 cm)(15 cm) = 75π cm².

Practice Test

1. Find a cone’s lateral surface area with a radius of 2 cm and a slant height of 3 cm.

2. A cone has a radius of 6 cm and a slant height of 8 cm. What is its lateral surface area?

3. If the cone’s radius is 4 cm and its slant height is 7 cm, calculate the lateral surface area. (Use: π = 3.14)

4. Calculate a cone’s slant height (L) given r= 8 m and h= 12 m. (Round off your answer to the nearest tenths)

5. A cone-shaped tent has a radius of 10 feet and a slant height of 15 feet. What is the lateral surface area?

Answers:

1. 6π cm²

2. 48π cm²

3. 87.92 cm²

4. 14.4 m

5. 150π square feet

Frequently Asked Questions (FAQs)

How do we differentiate the total surface area of a cone from the lateral surface area of a cone?

A cone’s lateral surface area refers to the cone’s curved part, excluding the base. In contrast, the total surface area includes both the curved surface and the base.

Can I find the lateral surface area of a cone if I only have the radius and the height?

To find the lateral surface area, you need the slant height, not the height. However, if you have the height (h) and the radius (r), you can use the Pythagorean theorem to compute the slant height (L) if the cone is a right circular cone.

Does the formula for a cone’s lateral surface area apply to all cones?

The formula applies to right circular cones where the vertex or apex is directly above the centre of the base. For other cones, the calculation may be more complex.

Why do we need to know the lateral surface area of a cone?

Calculating a cone’s lateral surface area has many practical applications, such as determining the amount of material needed to make a conical tent or materials to cover a conical surface.

Is the unit of the lateral surface area always in square units?

Yes, the lateral surface area, like all areas, is always expressed in square units, whether square centimeters, square inches, square feet, or any other square unit of measurement.

Recommended Worksheets

Surface Area of a Cone (Christmas Themed) Math Worksheets
Lateral Surface Area of a Cone (Day of the Dead Themed) Math Worksheets
Surface Area of a Sphere (Songkran Festival Themed) Math Worksheets