Introduction
The study of geometry often involves calculating areas and volumes of different shapes. Among these shapes, the cylinder is a common three-dimensional figure significant in many areas of life. One particular attribute of the cylinder, the Lateral Surface Area (LSA), is a crucial concept in geometry.
Grade Appropriateness
The concept of the lateral surface area of a cylinder is typically introduced around the 7th to 8th-grade level as students become more comfortable with concepts of area and begin to explore the dimensions beyond length and width.
Math Domain
This topic falls under the domain of Geometry concerned with the properties, measurement, and relationships of points, lines, angles, surfaces, and solids.
Applicable Common Core Standards
The relevant Common Core Standards for this topic are:
7.G.B.6: “Solve real-world and mathematical problems involving area, volume and surface area of two- and three-dimensional objects composed of triangles, quadrilaterals, polygons, cubes, and right prisms.”
8.G.C.9: “Know the formulas for the volumes of cones, cylinders, and spheres and use them to solve real-world and mathematical problems.”
Definition of the Topic
The cylinder’s lateral surface area is the area of the curved surface that wraps around the cylinder, excluding the two circular bases. In essence, it is the ‘wrapper’ that goes around the cylinder.
Key Concepts
Lateral Area: The area of the side of the cylinder. It is equal to the height (h) of the cylinder multiplied by the circumference of the base.
To calculate the Lateral Surface Area (LSA) of a cylinder, we use the formula:
LSA = 2πrh
where; r = radius, h = height, and π = Pi (approximately 3.14).
Discussion with Illustrative Examples
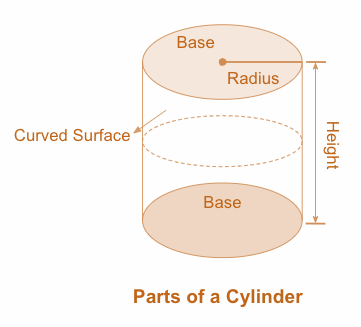
A cylinder is composed of a curved surface and two flat circular bases. A cylinder has two types of surface area: the curved or lateral surface area and the total surface area.
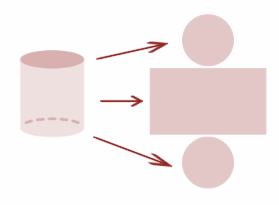
A cylinder’s curved or lateral surface area is the area occupied by the curved surface. In the figure above, the curved surface becomes a rectangle when flattened, with its length as the circumference of the base and its width as the height of the cylinder.
Therefore, to get the lateral surface area (LSA), we multiply the base’s circumference and the cylinder’s height.
Lateral Surface Area (LSA) = 2πrh
where;
r = length of the cylinder’s radius
h = height of the cylinder
π ≈ 3.14
Let us take an example:
Imagine a can of paint. The can is cylindrical. If we want to create a label that wraps perfectly around the can (ignoring the top and bottom), we need to calculate the LSA of the cylinder.
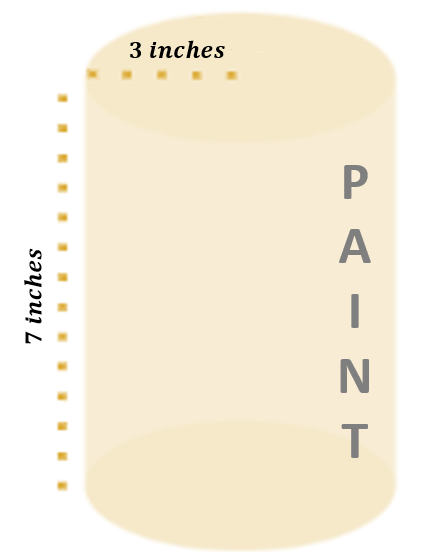
Suppose the can of paint has a radius of 3 inches and a height of 7 inches. Using our formula, we can calculate the LSA.
LSA=2πrh
LSA=(2)(3.14159 )(3 in)(7 in)
LSA≈131.95 in2
So, we would need a label about 131.95 square inches to wrap around the can perfectly.
Remember always to write the unit of measurement on your final answers! Since we’re talking about areas, the answers should be in square units.
Examples with Solution
Example 1
Find the lateral surface area of a cylindrical water tank with a radius of 2 meters and a height of 10 meters. (Use: π=3.14)
Solution
LSA= 2πrh
LSA=(2) (3.14)(2)(10)
LSA ≈ 125.6 m2
Hence, the lateral surface area of the cylinder is 125.6 square meters.
Example 2
Calculate the lateral surface area of the given cylinder. Use π = 3.14.
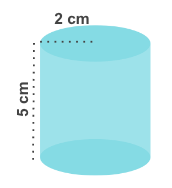
Solution
C= 2πrh
C=(2)(3.14)(2)(5)
C= 62.8 cm2
Therefore, the lateral surface area is 62.8 cm2.
Example 3
Calculate the lateral surface area of the given cylinder. Use π = 3.14.
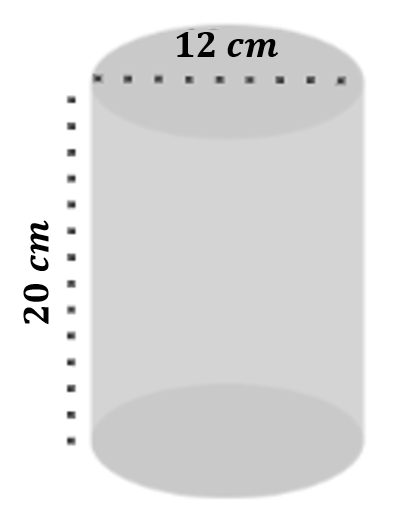
Solution
The radius is one-half of the diameter, so the radius is 12 ÷ 2 = 6 cm.
C= 2πrh
C=(2)(3.14)(6)(20)
C= 753.6 cm2
Therefore, the lateral surface area is 753.6 cm2.
Real-life Application with Solution
Cylinders are common in everyday life, from cans of food to gas cylinders. One real-life application of calculating the LSA of a cylinder is in the packaging industry.
Example: A packaging company needs to design a wrapper for a cylindrical box with a height of 15 cm and a diameter of 10 cm. What is the area of paper needed for the wrapper? (Use π = 3.14)
Solution
First, we must find the radius of the base of the cylindrical box. Since the radius is one-half of the diameter, r = 10/2 = 5 cm.
Using our formula, we can calculate the LSA.
LSA= 2πrh
LSA=(2) (3.14)(5 cm)(15 cm)
LSA= 471 cm2.
So, the company would need a piece of paper that is 471 cm2 to wrap the cylindrical box.
Practice Test
Here are a few problems to practice calculating the LSA of a cylinder.
1. Calculate the LSA of a cylinder with a height of 8 cm and a radius of 4 cm.
2. Calculate the LSA of a cylinder with a radius of 1.5 m and a height of 6 m.
3. Calculate the LSA of a cylinder: height=10 cm and diameter=12 cm.
4. Calculate the LSA of a cylinder with a diameter of 20 m and a height of 25 m.
5. A cylindrical pillar in a building has the following dimensions: height = 4 meters, diameter = 2 meters. Calculate the LSA. Use π = 3.14.
Answers:
1. 64π cm2
2. 18π m2
3. 120π cm2
4. 500π m2
5. 25.12 m2
Frequently Asked Questions (FAQs)
What differentiates the total surface area from the lateral surface area of a cylinder?
The total surface area of a cylinder includes the areas of both circular bases and the curved surface around the cylinder. The lateral surface area only includes the area of the curved surface, excluding the bases.
What units do we use for the lateral surface area?
The units for the lateral surface area are the square units of the length used. For example, if the height and radius are given in centimetres, the LSA will be in square centimetres.
Can the lateral surface area of a cylinder be less than the base area?
Yes, it is possible if the height of the cylinder is less than the radius.
Is the lateral surface area formula the same for all cylinders?
The formula LSA = 2πrh is the same for all right circular cylinders. However, the formula might be different for cylinders that are not right or not circular.
What is the importance of π (Pi) in the formula for the lateral surface area?
Pi (π), a mathematical constant, represents the ratio of a circle’s circumference to its diameter. In the formula for the LSA of a cylinder, Pi is used because the lateral surface can be viewed as a rectangle rolled around the circular base, with one side being the circumference of the base (2πr) and the other side being the height (h).
Recommended Worksheets
Surface Area of a Cylinder (Christmas themed) Math Worksheets
Lateral Surface Area of a Cylinder (National Space Day Themed) Math Worksheets
Surface Area of Solid Shapes (Shipping/Delivery Themed) Math Worksheets









