Introduction
A cube’s surface area is an essential topic in geometry and mathematics as a whole. It allows us to understand how much material is needed to cover the cube or estimate its environmental interaction. This article shall give a comprehensive guide on the surface area of a cube, including grade appropriateness, mathematical domain, common core standards, definition, key concepts, illustrative examples, real-life applications, practice tests, and frequently asked questions.
Grade Appropriateness
The concept of surface area is typically introduced in middle school (grades 6-8), with students encountering the surface area of a cube, specifically around 6th or 7th grade.
Math Domain
This topic falls under geometry, a branch of mathematics concerned with sizes, shapes, properties of space, and relative positions of figures.
Applicable Common Core Standards
The following common core standards apply to the topic of the surface area of a cube:
6.G.A.4: Represent three-dimensional figures using nets made up of rectangles and triangles, and use the nets to find the surface area of these figures.
7.G.B.6: Solve real-world and mathematical problems involving area, volume, and surface area of two- and three-dimensional objects composed of triangles, quadrilaterals, polygons, cubes, and right prisms.
Definition of the Topic
The sum of the area of a cube’s six faces makes up its total surface area. A cube has six equal square faces, and its total surface area can be determined by measuring the area of one face and multiplying it by six.
Key Concepts
A cube is a three-dimensional (3D) shape with six equally sized square faces.
The total surface area (TSA) is the area of all the external faces of a three-dimensional object.
To find a cube’s total surface area (TSA), solve the area of one face and multiply it by six.
The lateral surface area (LSA) is the area of all the external faces of a three-dimensional object, excluding the top and base surfaces.
To find a cube’s lateral surface area (LSA), solve the area of one face and multiply it by four.
Discussion with Illustrative Examples
Cube as a Solid Figure
Three-dimensional solid figures have length, width, and height. Cubes, pyramids, prisms, cones, spheres, etc., are a few of the most well-known solid shapes.
A cube has six equal square faces. A cube has equal-length sides on each side.
Cube is also a regular hexahedron and is part of platonic solids.
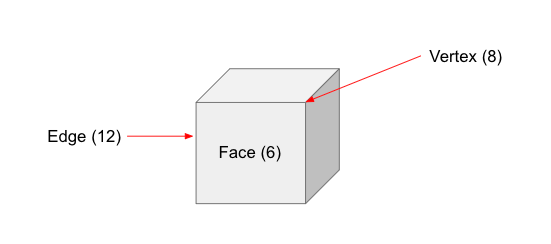
It has twelve edges — a common boundary shared by the faces of a cube.
It has eight vertices — the point where three edges meet.
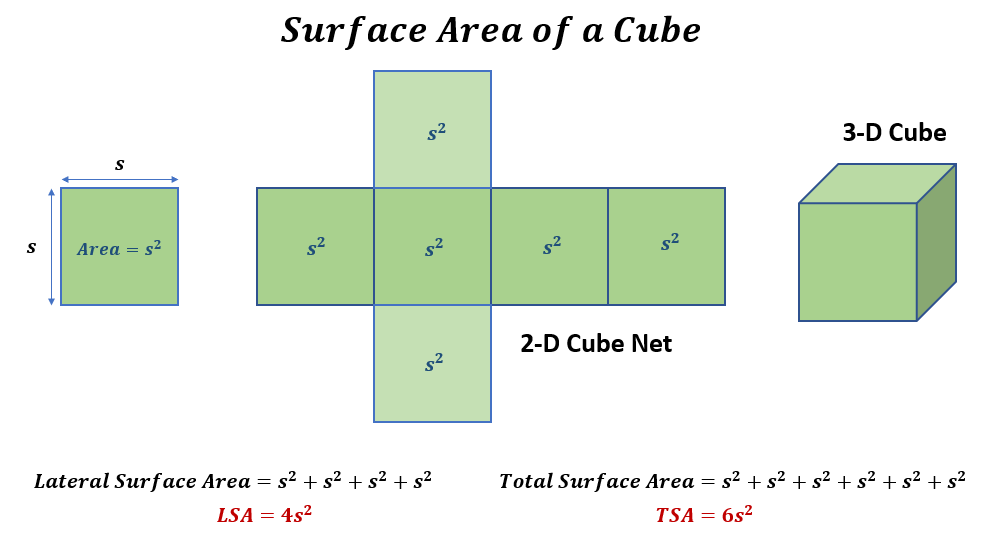
Surface Area Formulas
Let us denote the length of each side as “s.” To find the area of one square face, we’ll use the formula for the area of a square: A = s². Since there are six faces, we can find the total surface area using the formula: Total Surface Area (TSA) = 6s². The lateral surface area, on the other hand, is calculated using the formula: Lateral Surface Area (LSA) = 4s² since it refers to the area covered by the four side faces of a cube.
Let us consider a cube with a side length of 5 cm. Calculating its total surface area, we have,
Total Surface Area = 6s²
Total Surface Area = 6(5 cm)²
Total Surface Area = 6(25 cm²)
Total Surface Area = 150 cm²
And for its lateral surface area, we’ll have,
Lateral Surface Area = 4s²
Lateral Surface Area = 4(5 cm)²
Lateral Surface Area = 4(25 cm²)
Lateral Surface Area = 100 cm²
Hence, a cube with a side length of 5 cm has a total surface area of 150 cm2 while its lateral surface area is 100 cm².
Finding the side length of a cube using its surface area
A cube’s total surface area is 96 cm². What is its side length?
Total surface Area of a Cube = 6s2
96 cm2 = 6s2
$\frac{96}{6}$ cm2 = $\frac{6}{6}$s2
16 cm2 = s2
$\sqrt{16 cm^2}$ = $\sqrt{s^2}$
4 cm = s
Therefore, the side length of a cube can be calculated using the formula: $\sqrt{\frac{Total\ Surface\ Area}{6}}$.
Examples with Solution
Example 1
Determine the lateral surface area and total surface area of each cube.
| a. | b. | c. |
Solution
| a. LSA = 4s² LSA = 4(3 cm)² LSA = 4(9 cm²) LSA = 36 cm² TSA = 6s² TSA = 6(3 cm)² TSA = 6(9 cm²) TSA = 54 cm² | b. LSA = 4s² LSA = 4(5.5 in)² LSA = 4(30.25 in²) LSA = 121 in² TSA = 6s² TSA = 6(5.5 in)² TSA = 6(30.25 cm²) TSA = 181.5 in² | c. LSA = 4s² LSA = 4(8 m)² LSA = 4(64 m²) LSA = 256 m² TSA = 6s² TSA = 6(8 m)² TSA = 6(64 m²) TSA = 384 m² |
Example 2
Solve the surface area of a cube with a side length of 4 cm.
Solution
Total Surface Area = 6s²
Total Surface Area = 6(4 cm)²
Total Surface Area = 6(16 cm²)
Total Surface Area = 96 cm²
Therefore, a cube’s total surface area with a side length of 4 cm is 96 cm².
Example 3
Solve for the total surface area of the given cube.
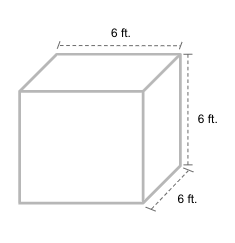
Solution
To solve for the cube’s total surface area, use the formula TSA = 6s2,
TSA = 6(6 ft)2
TSA = 6(36 ft2)
TSA = 216 ft2
Real-life Application with Solution
Problem 1
Consider that you need to wrap a present that has a cube-shaped shape and 10-inch sides. To determine how much wrapping paper is needed, you need to find the total surface area of the cube.
Solution
TSA = 6s²
TSA = 6(10 in)²
TSA = 6(100 in²)
TSA = 600 in²
Therefore, the total surface area is 600 in².
Problem 2
Larry has a cube-shaped container with a total surface area of 9600 cm2. Find the length of each side.
Solution
Since we know the total surface area, we can use the formula: Side length of a cube =$\sqrt{\frac{Total\ Surface\ Area}{6}}$. So,
Side Length = $\sqrt{\frac{9600}{6}}$
Side Length = $\sqrt{1600}$
Side Length = 40 cm
Hence, each side of the cube-shaped container is 40 cm long.
Practice Test
1. Solve for the total surface area of a cube given its side length of 7 cm.
2. Calculate the lateral surface area of a cube with a side length of 5 m.
3. Determine the total surface area of a cube with a side length of 6.5 ft.
4. A cube has a total surface area of 54 m². What is the length of each side?
5. Suppose the total surface area of a cube is 150 cm²; what is the volume of the cube?
Answers:
1. TSA = 294 cm2
2. LSA = 100 m2
3. TSA = 252.5 ft2
4. Side Length = 3 m
5. Volume of the Cube = 53 = 125 cm3
Frequently Asked Questions (FAQs)
Can the surface area of a cube ever be negative?
No, the surface area is always a positive value, representing a physical measurement.
Is the surface area of a cube always a whole number?
No, the surface area of a cube is not always a whole number. If the cube’s side length is a whole number, then the surface area will be a whole number. However, if the side length is a fraction or a decimal, the surface area may also be a non-whole number.
Can the surface area of a cube be zero?
No, the surface area of a cube cannot be zero, as each face has a non-zero area.
Can two cubes with different side lengths have the same surface area?
No, two cubes with different side lengths will always have different surface areas, as the surface area and the square of the side length are directly proportional.
Is a cube’s surface area the same as its volume?
No, the surface area and volume of a cube are distinct properties. The total surface area is the total area of all six faces, while the volume is the amount of space enclosed by the cube.
Recommended Worksheets
Surface Area of a Cube (International Day of Education Themed) Math Worksheets
Lateral Surface Area of a Cube (Memorial Day Themed) Math Worksheets
Cube (Sukkot Themed) Math Worksheets









