Introduction
Each of us has neighbors. Some have a common wall between their apartments, some have a common fence. It can be said that apartments or fences are adjacent to each other. Adjacent can be many things, including angles.
When we look at a watch with an hour, minute, and second hand, we see a pair of adjacent angles.
When we look at an open book its covers and one of the pages form a pair of adjacent angles.
When we ride a bike, the three adjacent spokes of the wheel form a pair of adjacent angles.
Two roads at the T-junction, a tram rail and a sleeper, two cross-street signs, open scissors, all these real-life objects form adjacent angles.
Having such a variety of adjacent angles in everyday life, it is worth studying and understanding which properties these angles have and what can be done with using these properties.
Definition of adjacent angles
The word “adjacent” means “next” or “neighboring”. We can treat adjacent angles as angles that are next to each other.
Adjacent angles are a pair of angles that share a common side and vertex. Three things that need to be done to keep the angles adjacent:
- adjacent angles go in pairs;
- adjacent angles share the common arm;
- adjacent angles have the same vertex.
The following diagram shows two adjacent angles 1 and 2 with the common arm $\vec{OB}$ and common vertex O.
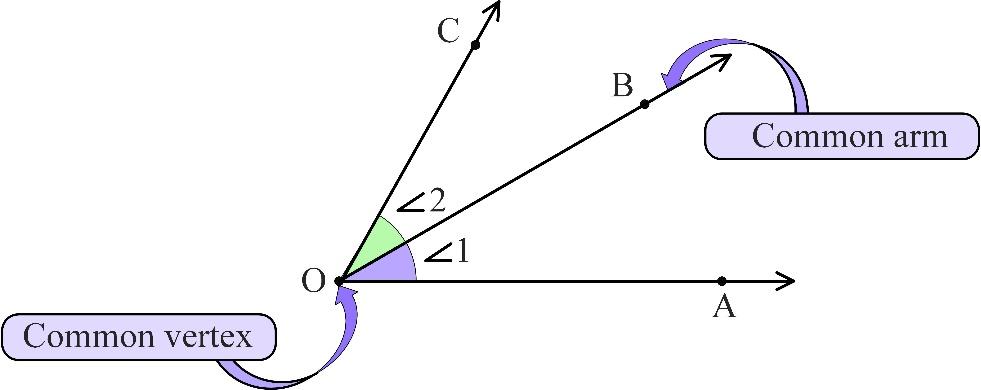
Adjacent angles never overlap
Every angle has one vertex and two arms, so it can have two possible adjacent angles, one attaching to each arm. In the diagram below, angles 2 and 3 are adjacent to angle 1: angles 1 and 2 share the common vertex O and common arm $\vec{OB}$, angles 1 and 3 share the common vertex O and common arm $\vec{OC}$.
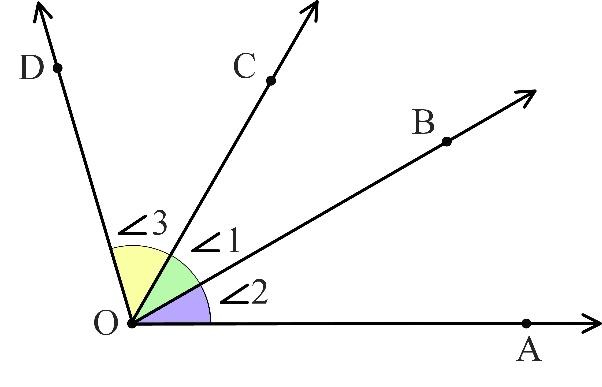
ANGLE ADDITION POSTULATE:
The angle addition postulate states that if point B is in the interior of AOC, then
m∠AOB+m∠ BOC=m∠ AOC
This postulate can be applied to any pair of adjacent angles.
Are there any restrictions on the measures of the adjacent angles? Let us think. If two adjacent angles never overlap, then their total measure cannot be greater than the measure of a full angle. So, if angles 1 and 2 are adjacent, then
m∠1+m∠2≤360°
Thus, we can obtain the following combinations of adjacent angles:
- two acute angles;
- two right angles;
- two obtuse angles;
- two straight angles;
- one acute angle and one right angle;
- one acute angle and one obtuse angle;
- one acute angle and one straight angle;
- one acute angle and one reflex angle (if their total measure does not exceed 360°);
- one right angle and one obtuse angle;
- one right angle and one straight angle;
- one right angle and one reflex angle (if their total measure does not exceed 360°);
- one obtuse angle and one straight angle;
- one obtuse angle and one reflex angle (if their total measure does not exceed 360°).
Two reflex angles can never form a pair of adjacent angles. Each of two arbitrary reflex angles has a measure greater than 180°, so the sum of the measures of these two reflex angles is always greater than 360° and angles overlap.
We already understood what the adjacent angles are. Let us consider the following example. Will the angles AOC and AOB shown in the figure be adjacent? Why?
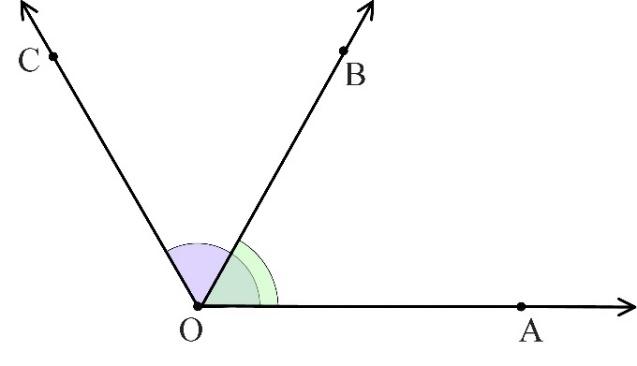
Formally, all the conditions of the definition are held:
- two angles AOC and AOB form a pair of angles;
- two angles AOC and AOB share the common vertex O;
- two angles AOC and AOB share the common arm $\vec{OA}$.
Are they adjacent? No, because they are overlapping. So, do not forget that two adjacent angles never overlap.
Examples of adjacent and not adjacent angles
Determining whether two angles are adjacent or not, you should clearly remember three things that these angles should have: be a pair of angles, have a common vertex, and a common arm. It is best to learn to understand whether the angles are adjacent or not on specific examples.
EXAMPLE: In each case determine whether the angles 1 and 2 are adjacent or not.

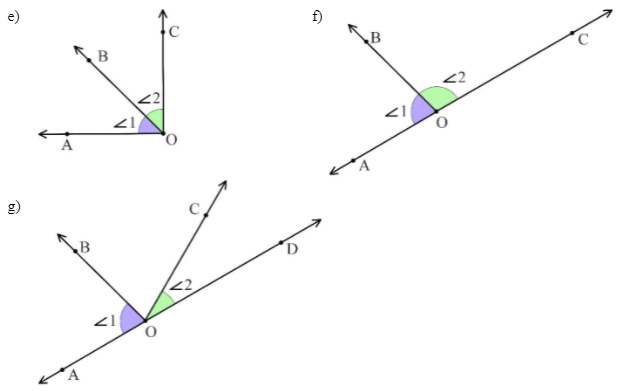
SOLUTION: a) Pair of angles ∠1 and ∠2 share the common vertex O and common arm $\vec{OB}$, so these angles are adjacent.
b) Pair of angles ∠1 and ∠2 share the common vertex O but do not share the common arm, so these angles are not adjacent.
c) Pair of angles ∠1 and ∠2 share the common vertex O and common arm $\vec{OB}$, so these angles are adjacent.
d) Pair of angles ∠1 and ∠2 share the common arm $\vec{OB}$ but do not share the common vertex, so these angles are not adjacent.
e) Pair of angles ∠1 and ∠2 share the common vertex O and common arm $\vec{OB}$, so these angles are adjacent.
f) Pair of angles ∠1 and ∠2 share the common vertex O and common arm $\vec{OB}$, so these angles are adjacent.
g) Pair of angles ∠1 and ∠2 share the common vertex O but do not share the common arm, so these angles are not adjacent.
Linear pair of angles
A linear pair of angles is a pair of adjacent angles formed when two lines intersect.
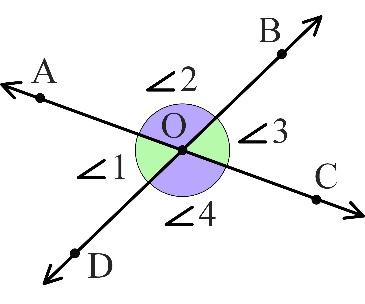
The above diagram shows two intersecting lines AC⃡ and BD⃡ which form four linear pairs of angles:
- angles 1 and 2;
- angles 2 and 3;
- angles 3 and 4;
- angles 4 and 1.
When two lines intersect, there are always four linear pairs of angles.
What is the same between a pair of adjacent angles and a linear pair of angles?

What is different between a pair of adjacent angles and a linear pair of angles?
| Pair of adjacent angles | Linear pair of angles |
| Not necessarily form a straight angle | Form a straight angle |
| The sum of the measures is the measure of the angle formed by the two non-common arms of adjacent angles | The sum of the measures is 180° |
Supplementary angles are two angles whose measures add up to 180°.
Supplementary angles are not necessarily adjacent angles. But every two adjacent angles whose measures add up to 180° are supplementary. Using this fact, we can state that
each linear pair of angles is a pair of supplementary angles
Take an arbitrary linear pair of angles, for example, angles 1 and 2. These two angles together form the straight angle DOB. The measure of a straight angle is always 180°. Therefore, by angle addition postulate,
m∠1+m∠2=m∠DOB
If m∠DOB=180°, then
m∠1+m∠2=180°
By the definition of supplementary angles, angles 1 and 2 are supplementary angles. In the same way, we can prove that each linear pair of angles is a pair of supplementary angles.
Now, we can outline the following basic properties of a linear pair of angles:
- every linear pair of angles is a pair of adjacent angles but an arbitrary pair of adjacent angles is not necessary a linear pair of angles;
- every linear pair of angles share a common vertex and a common arm between them;
- every linear pair of angles always forms a straight angle;
- every linear pair of angles is a pair of supplementary angles.
Note that the interior angle of the triangle and the corresponding exterior angle of the triangle together form a linear pair of angles and are always supplementary.
What is the same between a linear pair of angles and a pair of supplementary angles?

What is different between a linear pair of angles and a pair of supplementary angles?
| Linear pair of angles | Pair of supplementary angles |
| Share a common vertex | Not necessarily share a common vertex |
| Share a common side | Not necessarily share a common side |
| Is a pair of adjacent angles | Not necessarily is a pair of adjacent angles |
Complementary angles
Complementary angles are two angles whose measures add up to 90°.
Complementary angles are not necessarily adjacent angles. But every two adjacent angles whose measures add up to 90° are complementary.
In geometry, there are two types of complementary angles:
- two adjacent complementary angles;
- two non-adjacent complementary angles.
ADJACENT COMPLEMENTARY ANGLES:
Two complementary angles with a common vertex and a common arm are called adjacent complementary angles.
In the figure given below, AOB and BOC are adjacent angles as they have a common vertex O and a common arm $\vec{OB}$.

They also together form the right angle AOC. Thus, the measures of angles AOB and BOC add up to 90° and these two angles are adjacent complementary angles.
NON-ADJACENT COMPLEMENTARY ANGLES:
Two complementary angles which are not adjacent are called non-adjacent complementary angles.
In the figure given below, AOB and COD are non-adjacent angles as they have a common vertex O and do not have a common arm.
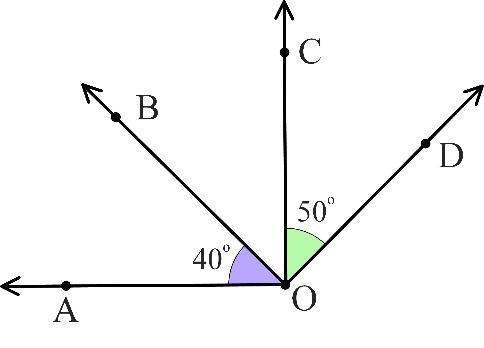
The measures of angles AOB and COD add up to 90°, so, these two angles are complementary. Therefore, angles AOB and COD are non-adjacent complementary angles.
Properties of adjacent angles
The following properties of adjacent angles help us identify whether the angles are adjacent and investigate these angles.
PROPERTIES:
- Adjacent angles share a common arm.
- Adjacent angles share a common vertex.
- Adjacent angles never overlap.
- All common points of two adjacent angles lie on the common arm.
- Adjacent angles can be complementary (their measures add up to 90°) or supplementary (their measures add up to 180°).
Vertical and adjacent angles
When two lines intersect, two pairs of opposite angles are formed. These angles are called vertical angles.

The above diagram shows two intersecting lines AC⃡ and BD⃡ which form two pairs of vertical angles:
- angles 1 and 3;
- angles 2 and 4.
When two lines intersect, two vertical angles are always congruent.
This statement is known as the vertical angle theorem. Let us prove that angle 1 is congruent to angle 3.
Since angles 1 and 2 form a linear pair of angles, they are supplementary angles and
m∠1+m∠2=180°
Since angles 2 and 3 form a linear pair of angles, they are supplementary angles and
m∠2+m∠3=180°
By the transitive property, if m∠1+m∠2=180° and m∠2+m∠3=180° , then
m∠1+m∠2=m∠2+m∠3
Subtract m∠2 from both sides of the above equality:
m∠1=m∠3
Using the definition of congruent angles,
∠1≅∠3
In the same way, we can prove that the remaining two vertical angles are congruent too.
What is the same between adjacent and vertical angles?

What is different between adjacent and vertical angles?
| Adjacent angles | Vertical angles |
| Share a common side | Do not share a common side |
| Formed when one arm of one angle is the arm of another, but the other arm is not. | Formed when two lines intersect |
| Not necessarily congruent | Are congruent |
| The sum of the measures is the measure of the angle formed by the two non-common arms of adjacent angles | Have the same measures |
FAQs
1. Which angles are called adjacent?
Adjacent angles are a pair of angles that share a common side and vertex. Three things that need to be done to keep the angles adjacent: adjacent angles go in pairs, adjacent angles share the common arm, and adjacent angles have the same vertex.
2. Could three angles be adjacent?
Three angles can be adjacent pairwise, but all together they are not adjacent, because adjacent angles are pairs of angles.
3. Can two obtuse angles be adjacent?
Any two obtuse angles that have a common vertex and a common arm are adjacent – the sum of their measures is less than 360°.
4. Can two reflex angles be adjacent?
Any two reflex angles with a common vertex and a common arm are not adjacent – the sum of their measures is greater than 360°.
5. Is the sum of the measures of two adjacent angles 180°?
No, the sum of the measures of two adjacent angles could be an arbitrary number of degrees, not necessarily 180°. To 180 degrees add up only two adjacent supplementary angles.
6. When two lines intersect, is there a relationship between two vertical angles and a linear pair of angles?
A linear pair of angles are always adjacent angles that add up to 180°. Two vertical angles are always opposite congruent angles, one of these angles belongs to a linear pair of angles. If you know the measures of one of the angles formed when two lines intersect, then you know the measures of all four angles.
7. Are the vertical angles adjacent?
Never. Vertical angles only have a common vertex but never have a common arm.
8. What is the difference between complementary and supplementary angles?
The measures of two complementary angles add up to 90° while the measures of two supplementary angles add up to 180°.
Quiz
- Two congruent angles are adjacent. What could be the maximum measure of each angle?
SOLUTION: If two angles are congruent, then they are both of the same type. We already know that two reflex angles cannot form a pair of adjacent angles as the sum of their measures is greater than 360°.
If these angles are not reflex, then consider the following by size angles – adjacent straight angles. When we take two congruent straight angles each of them has the measure of 180° and they add up to 360°. This is possible, so the maximum measure of each of two congruent adjacent angles could be 180°.
ANSWER: 180°
- In each case determine whether angles 1 and 2 are adjacent or not.

SOLUTION: a) Pair of angles ∠1 and ∠2 share the common vertex O but do not share the common arm, so these angles are not adjacent.
b) Pair of angles ∠1 and ∠2 share the common vertex O but they overlap, so these angles are not adjacent.
c) Pair of angles ∠1 and ∠2 share the common vertex O and common arm $\vec{OB}$, so these angles are adjacent.
d) Pair of angles ∠1 and ∠2 share the common vertex O and common arm $\vec{OB}$, so these angles are adjacent. Moreover, these angles are complementary.
ANSWER: a) not adjacent b) not adjacent c) adjacent d) adjacent
- In each case, state whether adjacent angles 1 and 2 are supplementary or not.
a) m∠1=45°, m∠2=135°;
b) m∠1=105°, m∠2=95°.
SOLUTION: Add the measures of the given angles. If the sum of the measures is 180°, then the given angles are supplementary, if the sum of the measures is not 180°, then the given angles are not supplementary.
a) m∠1+m∠2=45°+135°=180°
In this case, angles 1 and 2 are supplementary angles.
b) m∠1+m∠2=105°+95°=200°≠180°
In this case, angles 1 and 2 are not supplementary angles.
ANSWER: a) supplementary b) not supplementary
- In each case, state whether adjacent angles 1 and 2 are complementary or not.
a) m∠1=64°, m∠2=36°;
b) m∠1=25°, m∠2=65°.
SOLUTION: Add the measures of the given angles. If the sum of the measures is 90°, then the given angles are complementary, if the sum of the measures is not 90°, then the given angles are not complementary.
a) m∠1+m∠2=64°+36°=100°≠90°
In this case, angles 1 and 2 are not complementary angles.
b) m∠1+m∠2=25°+65°=90°
In this case, angles 1 and 2 are not complementary angles.
ANSWER: a) not complementary b) complementary
- Two lines a and b intersect. If every two adjacent angles are congruent, what is the measure of each of these angles? What can you say about lines a and b?
SOLUTION: If two lines a and b intersect, then they form four linear pairs of angles: ∠1 and ∠2, ∠2 and ∠3, ∠3 and ∠4, ∠4 and ∠1.
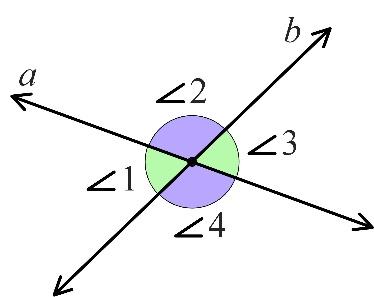
If every two adjacent angles are congruent, then
∠ 1≅ ∠2, ∠2≅∠3, ∠3≅∠4, ∠4≅∠1
By the transitive property,
∠1≅∠2≅∠3≅∠4
All these four angles form the full angle at the common vertex. Using the angle addition postulate, the measures of all four angles add up to 360°, so
m∠1+m∠2+m∠3+m∠4=360°
Since all four angles are congruent, they all have the same measures and the measure of each such angle is $\frac{1}{4}$360°=90°.
ANSWER: 90°
Conclusions
- Two adjacent angles “meet” by a common arm in a common vertex.
- Two adjacent angles never overlap.
- Names of two adjacent angles always have the same letter in the middle because they share the common vertex.
- There are some special pairs of adjacent angles: complementary, supplementary, interior and corresponding exterior angles of a triangle, of a polygon.
- There are pairs of angles that are never adjacent: pairs of vertical angles.
- The measures of adjacent angles we add using the angle addition postulate – those measures add up to the measure of the whole angle formed by two non-adjacent arms of given angles.
- Two reflex angles can never be adjacent.
Recommended Worksheets
Adjacent Angles (Mardi Gras Themed) Math Worksheets
Complementary Angles (Lantern Festival Themed) Math Worksheets
Right Triangles (Halloween Themed) Math Worksheets









