Measuring angles with a protractor can be a confusing experience. There are many things to which you must pay attention. Understanding that angles are parts of circles is helpful, because then the design of the protractor makes sense. With a little practice, you will soon be measuring angles with ease.
What is a protractor?
A protractor is a measuring tool often made of translucent plastic or glass used to read, measure, and construct angles. The most common protractor is a semicircle-shaped scale ranging from 0° to 180°.
Protractors can have diameters ranging from two inches to more than twelve inches. They are typically made of brass, steel, wood, ivory, or plastic.
Angles are typically measured in degrees (°). More so, most protractors have 180 equal segments. However, some protractors are in radian or arcminute scale.
What is the origin of protractors?
The use of protractors dates back over 500 years. Although older instruments were used for angle measurement in addition to other mathematical pursuits, Thomas Blundeville introduced a tool specifically for measuring and constructing angles in his 1589 Briefe Description of Universal Mappes & Cardes. It is unclear whether Blundeville developed the protractor. However, it was written in his book that he used the protractor to create maps, particularly for nautical charts.
In the early 17th century, protractors were widely used by navigators and surveyors. Meanwhile, in 1810, Joseph Huddart, a US naval commander, produced a more advanced version of a protractor created to plot a ship’s position on a nautical chart. It was then called as a three-arm protractor. By the nineteenth century, machinists had developed a wide range of specialized protractors. Then in the 20th century, protractors had also become ubiquitous in school mathematics.
Warm Up
Recall what you have learned about angles already. Angles are sections of a full circle. Since a full circle measures 360º, an individual angle has to measure less than 360º, because it is part of a circle.
Estimating the approximate measurement of a circle before you actually measure it can be helpful. By comparing your actual answer to your estimated measurement, you can determine whether or not your answer is reasonable.
In this lesson you will estimate angle measurements, find actual measurements using a protractor, and draw angles of various sizes.
How to use a protractor?
Protractors can be used to read and measure different angles. Now, this section will help you understand how to properly use a protractor.
Reading angles in protractor
A protractor can be used to read angles by using its either inner or outer readings. The inner and outer reading of each angle is always a supplement of each other since the sum of it will always be 180°.
Now, here’s how we can read angles using a protractor.
- Place the center of the protractor to the vertex of any angle.
- Place the protractor’s baseline on the ray, which is the angle’s base.
- Determine if you will use the inner or outer reading. If the angle to be measured is on the left-hand side of the protractor’s center, then we need to use the outer reading. If the angle is formed on the right-hand side of the protractor’s center, use the inner reading.
Example #1
Using a protractor, read the angle given in the figure.
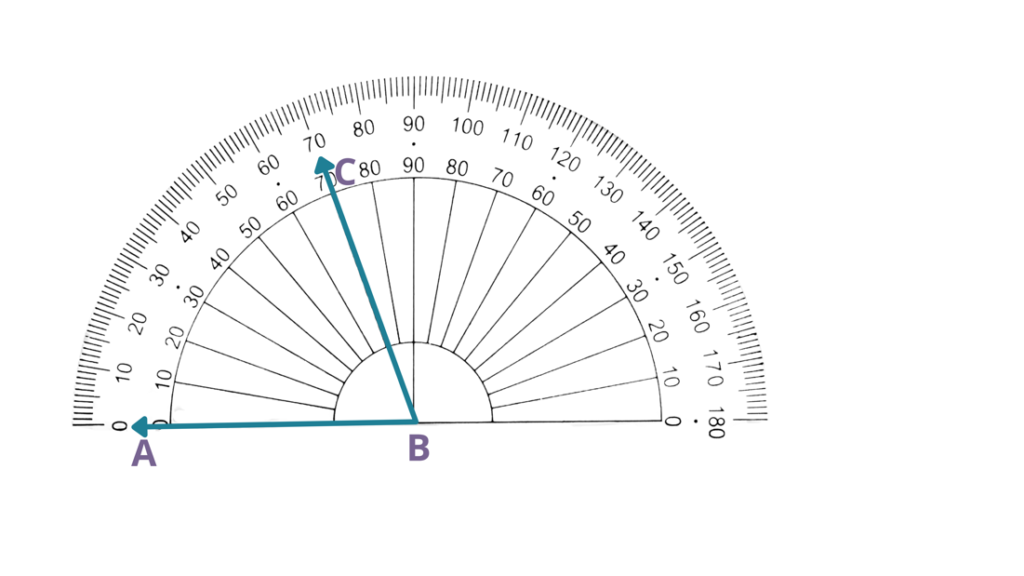
Solution
| Step-by-step Process | Explanation |
 | In the given figure, ABC is already placed in the center where the vertex is at B. |
| BA⃖ is on the left-hand side of the protractor’s center. | Since the base of the angle is at the left-hand side of the center of the protractor, then we will use the outer reading. |
| BC is pointed at 70°. | Since BC is pointed at exactly 70°, then ABC measures 70°. |
| Therefore, ABC measures exactly 70°. |
Example #2
Read the angle on a protractor.
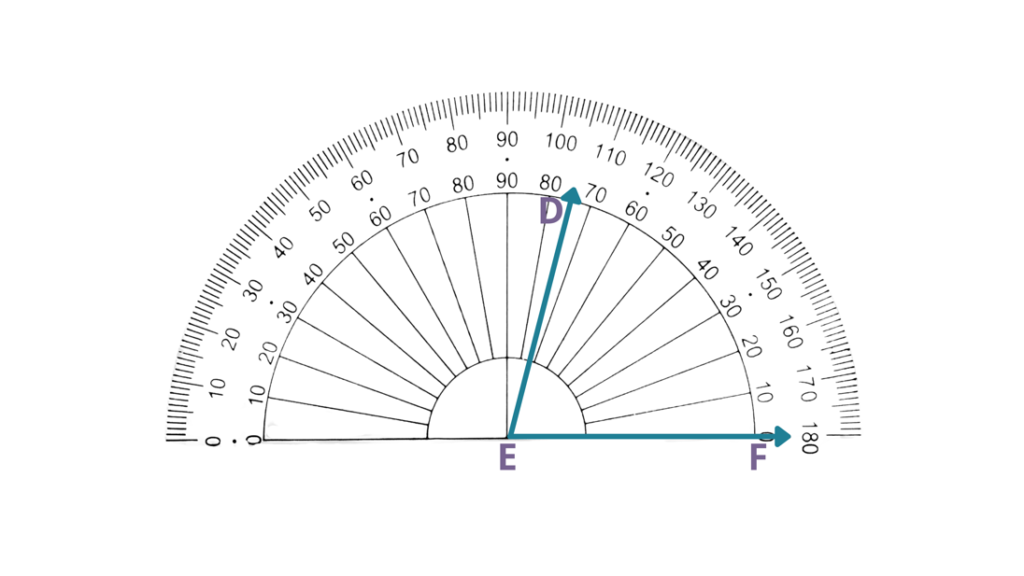
Solution
| Step-by-step Process | Explanation |
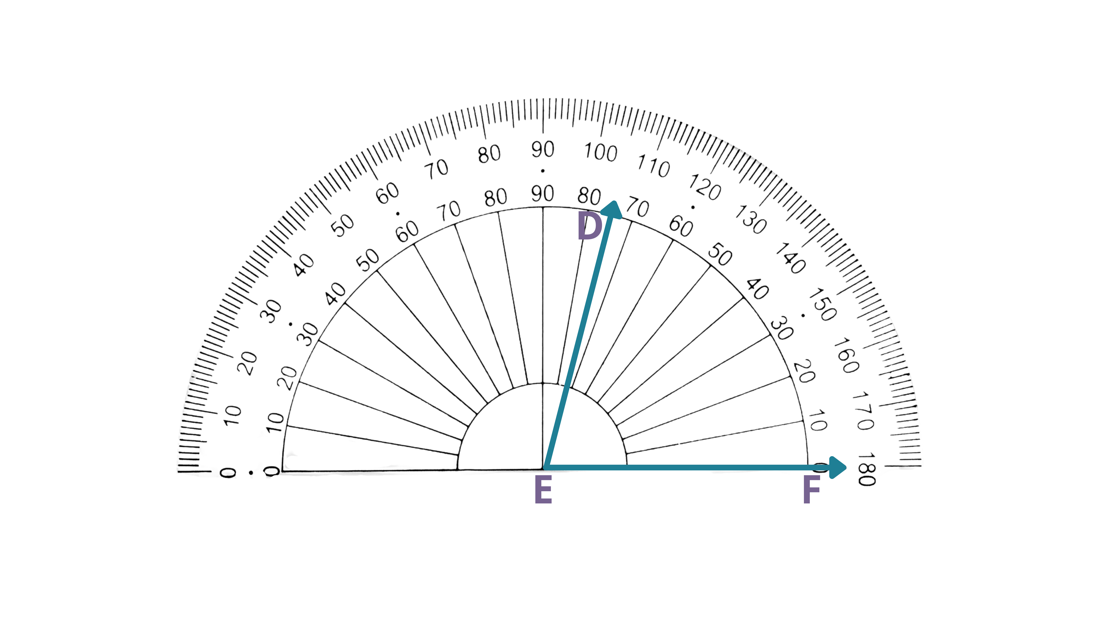 | In the given figure, DEF is already placed in the protractor’s center, where the vertex is at E. |
| EF is on the right-hand side of the protractor’s center. | Since the base of the angle is at the right-hand side of the center of the protractor, then we will use the inner reading. |
| ED is pointed in the middle of 70° and 80°. | Since ED is pointed at 75°, then FED measures 75°. |
| Therefore, FED measures 75°. |
Example #3
Read the angles on the protractor.
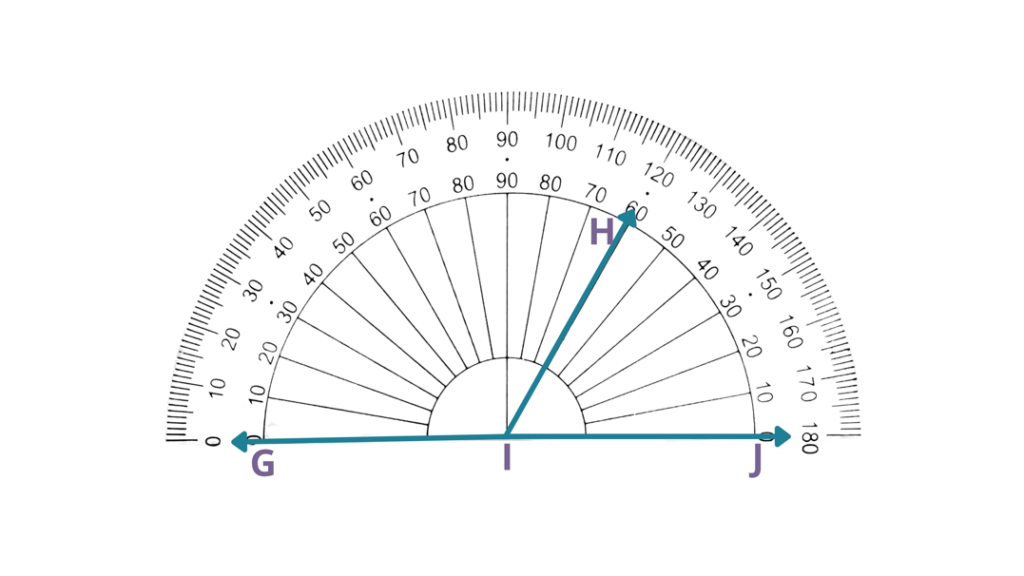
Solution
| Step-by-step Process | Explanation |
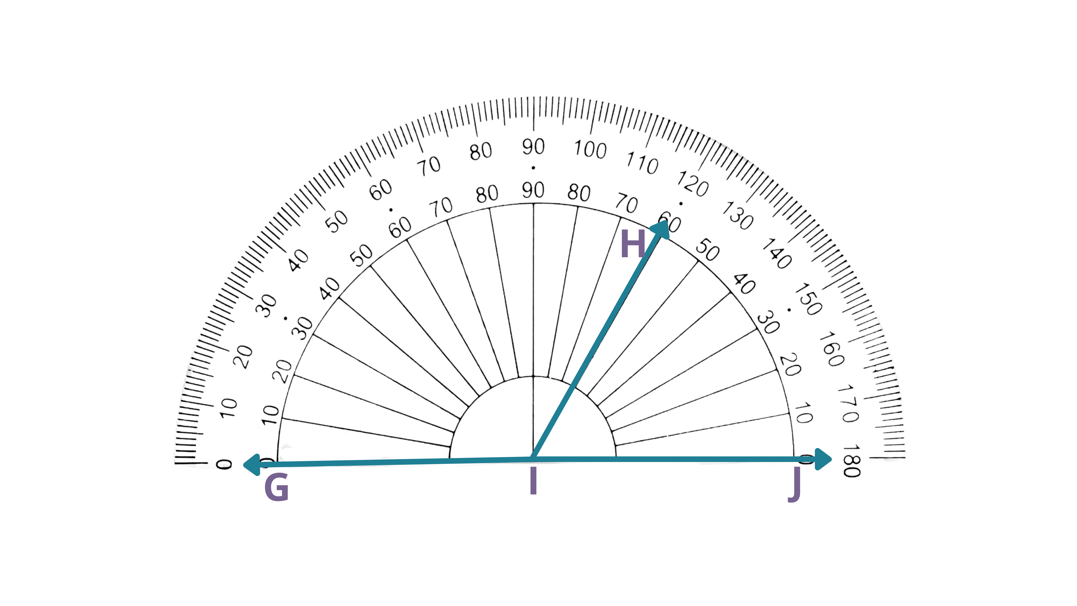 | In the given figure, the vertex of angles GIH and JIH is at I. Hence, we need to read the measure of the two angles. |
| IG⃖ is on the left-hand side of the protractor’s center. | Since the base of the angle is at the left-hand side of the center of the protractor, then we will use the outer reading. |
| IH is pointed at exactly 120°. | Using the outer reading, IH is pointed at exactly 120°, then GIH measures 120°. |
| IJ is on the right-hand side of the protractor’s center. | Since the base of the angle is at the right-hand side of the center of the protractor, then we will use the inner reading. |
| IH is pointed at 60°. | Using the inner reading, IH is pointed at exactly 60°, then JIH measures 60°. |
| Therefore, JIH measures 60°. |
Measuring angles using a protractor
To measure an angle using a protractor, you may consider following the steps below:
- Align the vertex of the angle on the midpoint of the protractor (usually a dot indicates the midpoint of the protractor).
- Align one side of the angle with 0 degrees on the protractor.
- Check where the other side of the angle intersects the number scale – that will determine the measure of the angle.
Make sure you’re reading from the correct set of numbers as most protractors have two sets of numbers: one from 0° to 180° and another from 180° to 0°.
Example
Using a protractor, measure the given angle.

Solution
| Step-by-step Process | Explanation |
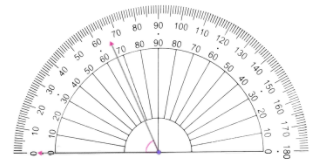 | Rotate the angle so that the base of the angle aligns with the protractor’s baseline. Then, make sure that the vertex of the angle is also aligned with the center of the protractor. |
 | Using the outer reading of the protractor, read where the arrow is pointed. Since it is pointed around 66°. |
| Therefore, the angle measure of the given figure is 66°. |
How to construct angles using a protractor?
To construct angles using a protractor, use the following steps:
- Draw the base of the angle.
- Make sure to align the baseline of the protractor to the base of the angle such that the protractor’s center is placed on the vertex of the angle.
- Put a mark to the measure of the angle that you want to create.
- Draw a line by connecting the vertex of the angle to the dot that you made from step 3.
Main Lesson: Using a Protractor
Now it’s time to talk about the tool that is used to measure angles. You may have wondered why it is shaped the way it is. Knowing that angles are measured by how many degrees of a circle are between the two rays, the shape starts to make more sense.
Help your children see the similarities between a half circle and the protractor. Show them that two protractors with the straight edges together would form a whole circle. Point out the similarities between the measurement markings and a regular ruler.

Line up the endpoint of the rays, called the vertex of the angle, with the crossed lines in the middle of the straight edge on the protractor. Line up the line that points to zero lined up with one of the rays that make the angle. Use the ruler on the curved edge to count the degrees until you reach the other ray in the angle.
Now that you understand how a protractor works, let’s look at a couple of angles and measure them:
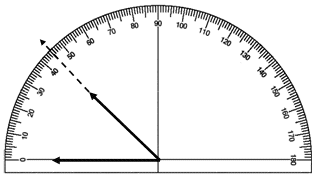
Whatever number of one-degree curves is an angle, that number equals the measurement of the angle.
Remind your children that it is very important to line up the protractor correctly so they can get a correct measurement. The crossed lines at the bottom of the straight edge must be matched up with the vertex (endpoint) where the two rays are joined.
Drawing Angles
A protractor can also be used to draw angles.
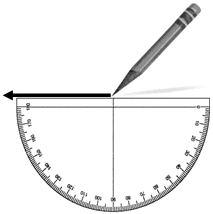
Example #1
Construct an acute angle using a protractor.
Solution
| Step-by-step Process | Explanation |
| Make a ray pointing to the left. | |
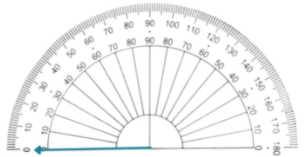 | Use the protractor to align the ray that you created such that the endpoint of the ray is at the center of the protractor. |
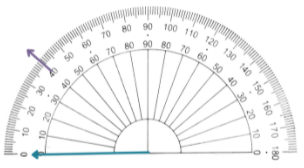 | Since we are asked to create an acute angle, mark any measure that is less than 90°. |
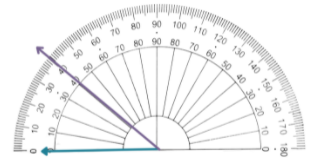 | Connect the created mark to the endpoint of the ray from step 1. |
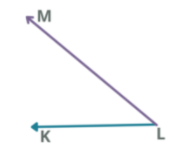 | Name the angle you created. In the given image, we have KLM or MLK that measures 40°. |
Example #2
Using a protractor, construct an angle that measures 150°.
Solution
| Step-by-step Process | Explanation |
| Make a ray pointing to the left. | |
 | Use the protractor to align the ray that you created such that the endpoint of the ray is at the center of the protractor. |
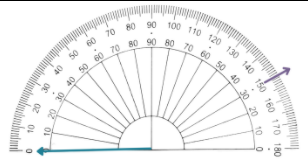 | Using the outer reading, create a mark in the 150°. |
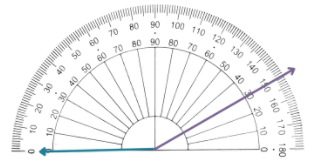 | Connect the created mark to the endpoint of the ray from step 1. |
 | Name the angle you created. In the given image, we have NOP that measures 150°. |
What are the different kinds of protractors?
There are different kinds of protractors that can also be used for different purposes.
Typical Protractor
The most typical and standard protractor is shaped as a half-circle that can measure 0° to 180°.
360° Protractor
A 360° protractor is designed as a whole circle wherein the readings are from 0° to 360°. This can be used to construct and measure reflex angles. More so, it provides more precision when measuring angles. It is often used in mechanical drawings, architecture, and even in meteorology.
Bevel Protractor
A bevel protractor is a graduated circular protractor made up of a beam, a dial, with one pivoting arm that is used to measure or mark off angles. Vernier scales are sometimes used to provide more exact readings. It is mostly used in architectural or mechanical drawing. However, since there is already modern software for drawing like CAD, the use of it is declining.
Protractors Through Time
The table shows some kinds of protractors that are used through time.
| NAME | DESCRIPTION | DATE MADE | IMAGE |
| Kern Semicircular Protractor | This protractor is made of German silver – which can also be called as nickel silver. It is graduated to a one-quarter degree along the outside edge and etched by tens from 350 to 0 to 190 in both directions, left to right and right to left. The horsecentre, or the center cross-plate comprises crosshairs that aid in the positioning of the protractor. More so, a moveable arm is attached to the center which has the Vernier scale allowing the user to read angles to one minute of arc. Lastly, the arm also includes a three-inch-long blade-like extension. The maker of this protractor is Kern & Co. | 1819 – 1895 |  Engineering & Drafting, digital photograph, National Museum of American History, https://americanhistory.si.edu/collections/object-groups/protractors/engineering-drafting. Accessed 15 Feb 2022. |
| Protractor signed by Cox | This protractor is made by W. C. Cox which is made of brass. It is a half-degree graded semicircular brass protractor. It is denoted by tens ranging from 10° to 170° in both directions, left to right and right to left. The small hole in the rectangular base of the protractor is used to locate the vertex of the angle being measured. | circa 1840 |  Engineering & Drafting, digital photograph, National Museum of American History, https://americanhistory.si.edu/collections/object-groups/protractors/engineering-drafting. Accessed 15 Feb 2022. |
| Rectangular Protractor | The angle markers of a rectangular protractor are along three edges of a rectangle rather than along the arc of a circle or half-circle. The device resembles a ruler and fits nicely into a pocket or instrument case. Other scales can be used in the rectangle’s interior and on both sides. It is graduated in single degrees and written by tens from 10° to 170° in both directions, left to right and right to left. More so, the scales in front of the protractor is marked as 18, 14, 38, 12, 58, 34, 78, and 1 inch to a foot. The protractor’s back has scales that divide an inch into 60, 50, 45, 40, 35, and 30 parts. These scales were also handy for drafting scales and reading them. Lastly, this protractor also has a diagonal scale for reading fractions of an inch and scales of cosines. | 19th century |  Engineering & Drafting, digital photograph, National Museum of American History, https://americanhistory.si.edu/collections/object-groups/protractors/engineering-drafting. Accessed 15 Feb 2022. |
| Isometric Protractor | An isometric protractor is used to draw three-dimensional objects from an angle where the scales on the three axes are equal. It is called as an isometric protractor because it only measures 30° angles. The arm can be positioned horizontally or at 150° (30° if measuring an angle opening to the right). | ca 1870 |  Engineering & Drafting, digital photograph, National Museum of American History, https://americanhistory.si.edu/collections/object-groups/protractors/engineering-drafting. Accessed 15 Feb 2022. |
| Lyman Protracting Trigonometer | This metal protractor is used by civil engineers to convert their data into drawings with minimal calculations. It is made up of about 32 inch long flat steel base bar, a semicircular protractor with a flat plate along the diameter that slides along the base bar, a long steel arm clamped to the center of the proctor, a sliding brass square that moves along the arm, and a tri-leaved scale that moves along the arm or along the set square. Each of the four metal springs has its own screw. The protractor plate is held to the base bar by two smaller springs, and the tri-leaved scale or set square is held to the arm by two bigger springs. The protractor is divided into half-degree increments and labeled in tens from 0° to 90° to 0° and 90° to 0° to 90°. Angle readings to one minute of arc are possible because of the attached vernier. The architect’s scales have ratios ranging from 1:10 to 1:60. Each scale is divided into tenths of a unit. This protractor is made by Heller & Brightly. | circa 1880 |  Engineering & Drafting, digital photograph, National Museum of American History, https://americanhistory.si.edu/collections/object-groups/protractors/engineering-drafting. Accessed 15 Feb 2022. |
| Brown & Sharpe Draftsman’s Protractor | This protractor is invented by Samuel Darling. It is divided into single degrees and marked in fives from 0 to 90 clockwise. Thirty additional unnumbered divisions stretch beyond the 90° mark. Angles can be measured to one minute of arc using a vernier on the frame. | 1889 – 1892 |  Engineering & Drafting, digital photograph, National Museum of American History, https://americanhistory.si.edu/collections/object-groups/protractors/engineering-drafting. Accessed 15 Feb 2022. |
| Brown & Sharpe Bevel Protractor | This version of the protractor is circular in shape and is placed within the irregularly shaped blade. An 11-1/2″ trapezoidal blade slides into the housing and is held in place by a screw on the protractor. The protractor is divided by single degrees and marked by tens from 0° to 90° to 0° to 90° to 0°. A vernier, attached by another screw, allows angle readings to five minutes of accuracy. | 1899 – 1949 |  Engineering & Drafting, digital photograph, National Museum of American History, https://americanhistory.si.edu/collections/object-groups/protractors/engineering-drafting. Accessed 15 Feb 2022. |
| Dietzgen Limb Protractor | Limb protractor is manufactured by Eugene Dietzgen Company. This quarter-circle-shaped German silver protractor is made of silver. It is broken into half-degree increments and labeled in tens from 0° to 90°. The protractor has flat bars on both sides. From the quadrant’s vertices, a moveable arm extends. This limb has a tab cut off to allow reading of the angle marks. The arm is held in place by a brass thumbscrew located near the origin point of the angle marks. | ca 1990 |  Engineering & Drafting, digital photograph, National Museum of American History, https://americanhistory.si.edu/collections/object-groups/protractors/engineering-drafting. Accessed 15 Feb 2022. |
| Kern Semicircular Protractor | This semicircular protractor is manufactured by Kern & Co. and is made from German silver. It is graduated in quarter-degree increments and denoted by tens ranging from 10 to 170 from left to right and right to left. The protractor’s lower edge is beveled, with a groove at the origin point. | early 20th century |  Engineering & Drafting, digital photograph, National Museum of American History, https://americanhistory.si.edu/collections/object-groups/protractors/engineering-drafting. Accessed 15 Feb 2022. |
| Semicircle Protractor by Post | This semicircular protractor is manufactured by Frederick Post Co. and is made from brass. It is divided into single degrees and indicated by tens from 0° to 180° clockwise and counterclockwise. The bottom border is recessed to allow for the placement of a pencil or pricker at the origin point. | 1920 – 1940 |  Engineering & Drafting, digital photograph, National Museum of American History, https://americanhistory.si.edu/collections/object-groups/protractors/engineering-drafting. Accessed 15 Feb 2022. |
| Brown & Sharpe 510 Draftsman’s Protractor | Instead of 30, this protractor has 40 unmarked divisions. | ca 1925 |  Engineering & Drafting, digital photograph, National Museum of American History, https://americanhistory.si.edu/collections/object-groups/protractors/engineering-drafting. Accessed 15 Feb 2022. |
What is the importance of using a protractor?
In Geometry, a protractor allows us to measure and determine the names of different angles. Different kinds of protractors are also used in various fields such as architecture, engineering, and meteorology.
Recap
- Angles are sections of a circle.
- Angles are measured in degrees.
- There are 360° in a circle.
- Individual angles measure less than 360°
- A protractor is used to measure angles.
- A protractor can also be used to draw an angle.
- It is important to line up the protractor correctly.
Recommended Worksheets
Obtuse Triangles (Toy Store Themed) Math Worksheets
Equilateral Triangles (Outer Space Themed) Math Worksheets
Angle Measurements (Cruise Ship Themed) Worksheets









