Area of a Square
A square is a quadrilateral that has four equal sides and four right angles.
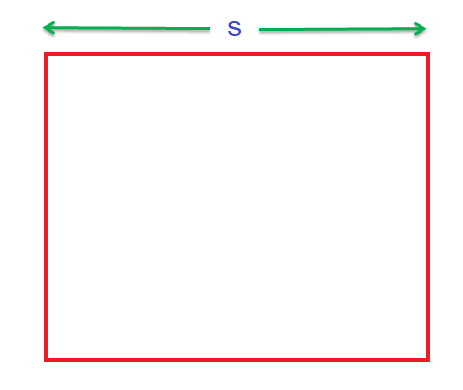
For a square whose side is of ‘s’ units:
Area of a Square = Side x Side = s2 sq. units
For example, if we have a square whose one side is 6 cm, its area would be calculated as:
Area = Side x Side = 6 x 6 = 36 cm2
Area of a Rectangle
A rectangle is a type of quadrilateral that equal opposite sides and four right angles.
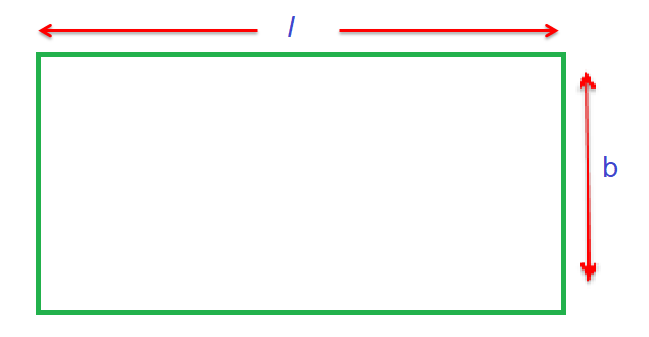
Area of a rectangle having length ‘l’ and breadth ‘b’ is given by l x b
For example, let us consider a rectangle having a length of 8 cm and a breadth of 7 cm as shown in the figure below.
Area of a Triangle
A triangle is a polygon that is made of three edges and three vertices. The vertices join together to make three sides of a triangle. The area occupied between these three sides is called the area of a triangle.
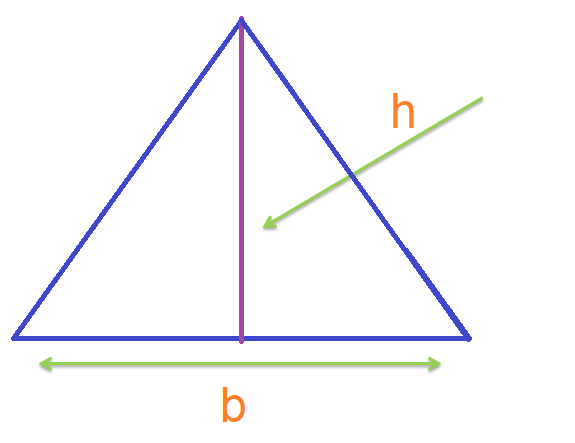
The area of a triangle is defined by: 1/2 x b x h
Where b = base of the triangle (or any one side of the triangle)
And
H = Height of the triangle from that base (or side)
The following figure illustrates the base and the height of a triangle:
The above formula is applicable irrespective of the fact whether a triangle is a scalene triangle ( having different sides), an isosceles triangle ( having two sides equal), or an equilateral triangle ( having all sides equal).
Let us understand this more through an example. Suppose we have a triangle that has one side as 6 cm and an altitude (height) of 8 cm on that base as shown in the following figure:
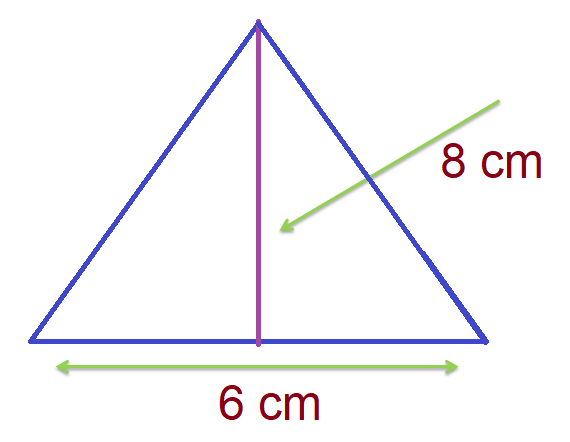
The area of this triangle is given by
1/2 x b x h
Where b = 6 cm and h = 8 cm
Therefore, Area = 1/2 x 6 x 8 = 24 cm2
Area of a Circle
The space occupied by a circle is called its area.
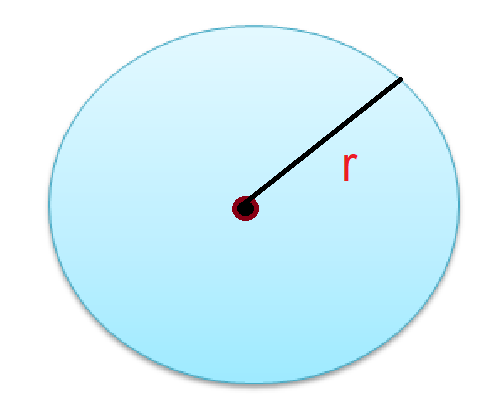
The area of a circle having a radius ‘r’ (The distance from the center to a point on the boundary) is given by πr2 where π = 22/7 or 3.14 (approx.)
For example, suppose we have a circle that has a radius of 7 cm as shown in the figure below.
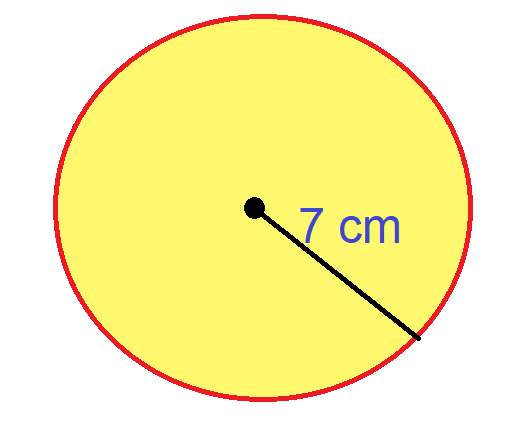
Its area is given by:
Area = πr2 = (22/7) x 7 x 7 = 154 cm2
Suppose, instead of the radius we are given the diameter of a circle, how do we calculate the area?
We know that in a circle, the radius is half of the diameter. Mathematically,
r = d/2, where ‘d’ is the diameter and ‘r’ is the radius.
So, we half the given diameter and obtain the radius.
Example
Suppose we are required to find the area of a circle having a diameter of 4.2 cm.
Here diameter (d) = 4.2 cm
By the relation between radius and diameter, we have, r = d/2.
Hence r = 4.2/2 = 2.1 cm
Now, area of this circle = = πr2 = (22/7) x 4.2 x 4.2 = 55.44 cm2
Circumference of a Circle
The length that equals the boundary of a circle is called its circumference. It is given by 2πr, where r is the radius. In other words, the circumference of a circle is what a perimeter is for other geometrical figures such as a rectangle of a square.
Let us consider a circle that has a radius of 7 cm. In order to find its circumference, we need to use the formula 2πr.
Hence, circumference of this circle = 2πr = 2 x (22/7) x 7 = 44 cm.
Note the units of perimeter and the area. While the units of area are always in square units in the case of perimeter they are always in the standard units of length such as m, cm, dm, km, etc.
Volume of Rectangular Prism
A polyhedron containing two pairs of congruent parallel bases is called a rectangular prism. It is considered to be a prism because of its cross-section along the length. The base of a rectangular prism is a rectangle. It has three dimensions as illustrated in the figure below:
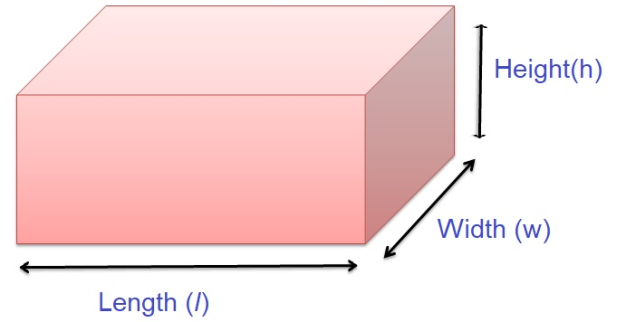
The volume of a rectangular prism is given by:
V = l x w x h
Where
l = Length of the base of the prism
w = width of the base of the prism
h = height of the prism
For example, we have a rectangular prism where the length of its base is 6 cm; the width of the base is 5 cm while its height is 4 cm. The volume would then be given by:
Volume (V) = l x w x h
Where
l = 6cm, w = 5cm and h = 4cm
Volume = 6 x 5 x 4 = 120 cu. cm
Not the units of the volume. The volume of any geometrical figure is always given in cubic units.
Volume of a Right Circular Cylinder
The quantity (in any form) that can be held up in a cylinder is called its volume. In other words, volume of a cylinder is the It is the space occupied by it. The base of a right circular cylinder is a circle on both ends that run parallel to each other as shown in the figure below.

Volume of a Right Circular Cylinder is given by:
| Volume = Area of its Base x Height of the Cylinder |
Since the base is a circle, its area is given by πr2
Therefore, the volume of a Right Circular Cylinder becomes πr2h
Example
Suppose we want to find the volume of a right circular cylinder whose radius at the base is 5 cm and the height of the cylinder is 7 cm.
The following figure illustrates the given dimensions of this cylinder.
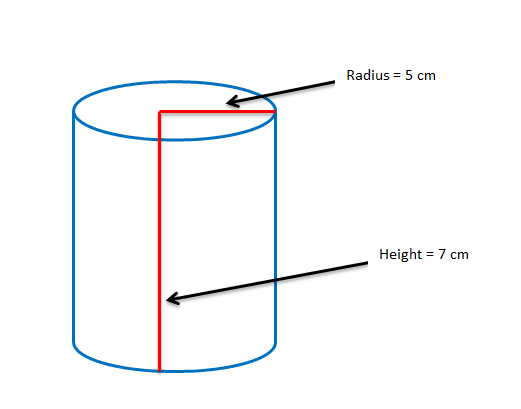
Its volume is given by πr2h = (22/7) x 5 x 5 x 7 = 550 cu. cm
Volume of Cone
A cone is a pyramid with a circular base. Its volume is given by 1/3πr2h where ‘r’ is the radius of the base of the cone and ‘h’ is its height.
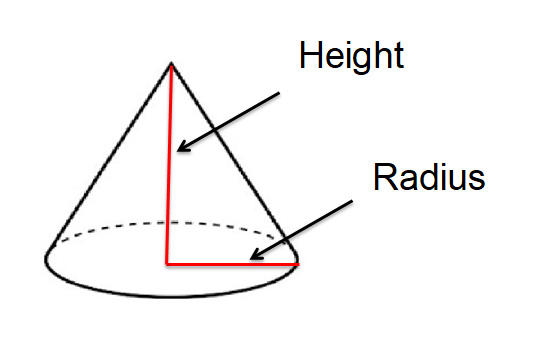
Suppose we want to calculate the volume of a cone having a radius of 6 cm and a height of 14 cm.
Its volume would be given by:
V = 1/3πr2h = (1/3) x (22/7) x 6 x 14 = 88 cu. cm
The above formulas can be summarised in the below table
The formulas listed below are commonly required in geometry to calculate lengths, areas and volumes. You can use these to help with your children’s math homework.
List of formulas
| Area of Square | = length2 (l x l) |  |
| Area of Rectangle | = length x height | 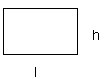 |
| Area of Triangle | = 1/2 x length x height | 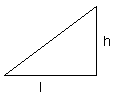 |
| Area of circle | = ?r2(? = 3.14 approximately) | 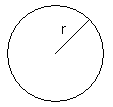 |
| Circumference of a circle | circumference = 2 r (? x diameter) |
|
| Volume of rectangular prism | = length x height x depth | 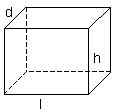 |
| Volume of cylinder | = area of base x height= ? (d/2)2 x h |  |
| Volume of cone | = 1/3 x area of base x height= 1/3 x ?(d/2)2 x h | 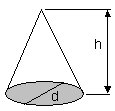 |









