Attribute | Definition, Examples, Techniques, Using Blocks

Classification was among the first concepts developed. A classification process involves discrimination, matching, and grouping based on attribute values and attributes. Following is a sampling of these attributes and attribute values at the quality level:

Shapes (square, circle, triangle, rectangle)
Sizes (large, small, big, little)
Weight (heavy, light)
Length (short, long)
Width (wide, narrow, thick, thin)
Height (tall, short)

The quantitative attributes would include general number concepts, such as many, few, more, less, and none, and later, more specific number values, such as sets of two, sets of ten, and greater than two etc.

In mathematics, an attribute is a characteristic or feature of an object that allows it to be grouped with other objects of a similar nature. It is typically used to describe an object’s size, shape, or color.

The concept of attributes is taught as early as kindergarten, where children are often given a set of blocks of varying colors, shapes, and sizes to sort by a specific attribute such as size, color, or shape, then asked to sort again by more than one attribute.

In summary, it is usually used to describe a geometric pattern and is used throughout the course of mathematical study to describe certain traits or characteristics of a group of objects, such as the area and measurements of a square or the shape of a football.

Early math concepts are explained as attributes of physical objects, primarily size, shape, and color, rather than abstract mathematical concepts. The first three of these attributes are discussed in kindergarten and the first grade.

A student, as they progress, should be able to identify all measurable attributes such as the length, capacity, and/or weight of an object. A piece of string, for example, has the measurable attribute of length. The length, capacity, and weight of a bag of candy can be measured since the height of the box and the amount of cereal it takes to fill the bag can be calculated, and the weight of the bag can be found.

While these basic concepts are later developed in higher mathematics, particularly geometry and trigonometry, it is still crucial that young mathematicians grasp the idea that objects can have traits and features in common that can aid them in sorting large groups of objects into smaller, more manageable groups.

This same concept will later be applied in higher mathematics to calculate totals of quantifiable attributes between groups of objects.

For example, observe the following picture of books.

From the above image, the traits of the books can be listed as:

Color – Red and Blue
Shape – Rectangle
Weight
Page count
Length & Breadth in a given unit

Commonly used terms

Measurable Attribute: Attributes that can be measured (like width, height, weight, temperature, length, volume, mass, area, temperature)

Sort or Classify: To group according to shared or common attributes

Defining vs Non-defining Attributes

When dealing with shapes, there are two types of attributes- defining and non-defining attributes. Defining attributes are the traits or properties that make a shape unique and distinct. In contrast, non-defining attributes include the shape’s color, orientation, size, etc.

Defining Attributes: number of sides, edges, faces, vertices/points, straight sides, closed figure

Non-defining attributes: color, overall size, and orientation

Attributes of a shape

Early mathematics involves understanding the concept of attributes and being able to differentiate between attributes of objects. It introduces the concept of patterns that allow us to associate objects together (or separate them) based on their characteristics, which later becomes useful in areas such as algebra (as well as many others), where we need to group various terms to simplify expressions and solve equations.

The most common way we can identify different attributes is by using shapes. Geometric shapes have attributes that define their characteristics visually and mathematically.

Different plane shapes have distinct attributes, such as the number of sides or corners (or vertices). A side is a straight line that forms part of a shape, a corner, and a vertex is where two sides meet.

In spite of knowing the most common shapes, before kindergarten, many children are unable to verbalize what makes a square different from a rectangle or a circle different from a triangle. They learn to describe shapes in terms of their sides and corners.

Triangles have three sides and three corners. Rectangles have four sides and four corners. They may notice that opposite sides are the same length.

Squares are rectangles with equal lengths on all four sides. A circle is a round shape that has no sides or corners. These attributes, as well as size, can be used to sort and classify shapes.

Let us take a look at another example. Consider a “square” as shown below. The attributes of a square are:

Reference: https://www.math.net/img/a/primary-math/area/square-inch/a.svg

Visual Attributes	Mathematical Attributes
The shape has 4 sides and 4 vertices All sides are equal Opposite sides are parallel	Each side measures 1 inch The angle between any two adjacent sides is 90 degrees.

Similarly, based on the attributes, we can determine the type of triangle:

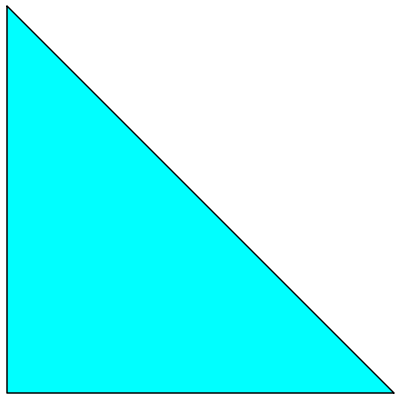
Type: Right angled triangle

The color of the triangle is blue
Two sides can be equal
The angle between the two sides is 90 degrees.
Common Attributes in Elementary Mathematics

Reference: https://upload.wikimedia.org/wikipedia/commons/thumb/7/7f/Green_equilateral_triangle_point_up.svg/900px-Green_equilateral_triangle_point_up.svg.png

Type: Equilateral triangle

The color of the triangle is grey
All 3 sides are equal
The angle between the two adjacent sides is 60 degrees

Type: Scalene triangle

The color of the triangle is red
All 3 sides are unequal
One of the angles between the two sides is more than 90 degrees

In geometry, besides the number of sides and angle measurements, shapes can be grouped according to several other attributes. As an example, the three triangles shown above are all different types of triangles. The blue triangle is a right-angled triangle, the green triangle is an equilateral triangle, and the red triangle is a scalene triangle.

Its Application

Children become acquainted with numbers first visually before comprehending them and understanding them. Identifying attributes of geometric figures and math expressions (such as symbols and operators) and translating them into numbers is the most important step in finding “attributes”.

Some fun facts:

In the study of star constellations, astronomers found common attributes between them which led to the names of famous constellations
A programming language’s functions & attributes are used to develop logic in computer programming and code writing

Using Attributes to Compare and Group Objects

Children must learn how similar shapes and patterns help group objects together, so they can then be counted, combined, or divided equally into different groups based on their attributes. This is particularly important in early childhood math lessons.

By observing the patterns and similarities of particular attributes of groups of objects, these core concepts provide a basis for simplifying complex equations, which is essential to understanding higher mathematics.

Consider the case of someone who had 10 rectangular flower planters that each measured 12 inches by 10 inches by 5 inches deep. This means that the total surface area of all the planters (the length times the width times the number of planters) would equal 600 square inches.

On the other hand, if a person had 10 planters that were 12 inches by 10 inches and 20 planters that were 7 inches by 10 inches. In order to quickly determine how much surface area all the planters have between them, it would be necessary to group the two different-sized planters by these attributes. As a result, the formula would be (10 X 12 inches X 10 inches) + (20 X 7 inches X 10 inches) since the two groups’ surface area must be calculated separately since their sizes and quantities differ.

Attributes and Variables

Here are some basic differences between the two:

An attribute is a characteristic of an object (person, thing, etc.). They are closely related to variables. While variables are sets of attributes that have a logical meaning.
A variable can be high or low, for instance, depending on the value of the attribute. An attribute could simply be the word “low” or “high”.
Attributes are intuitive, but variables are how the attribute is operationalized for purposes of further data processing.
Data are often represented by objects (rows of objects) and variables (columns of variables).

Introducing attributes to children

To educate children about shapes, they must go beyond the use of superficial shape labels and learn to recognize and specify the attributes of shapes. When children sort and classify shapes with the assistance of their teachers, they start to understand rules about shapes, such as, that a triangle has three sides and three angles (corners), that a cylinder has a rounded shape with two flat ends, or that a sphere has only one continuous curve. The idea that these sorts of precise distinctions can be made is not immediately apparent to young children; therefore, teachers must design activities to demonstrate this concept.

Knowledge of shape attributes contributes to a child’s ability to compose shapes (combining two congruent right triangles into a rectangle; constructing rectangles from two triangular prisms) and to decompose them (the reverse of composition actions). Both of these abilities contribute to a child’s ability to perform physical and mental transformations, which will be discussed later.

As already mentioned, a child starts to identify and recognize geometric attributes from a fairly early age. To start with, teachers introduce vertex, edge, and face so that students get a grasp of the concept. In spite of this, it seems that kids have a hard time answering questions about the attributes of geometric shapes. It’s common for them to mix up the vocabulary- they are unable to remember which are vertices and which are edges.

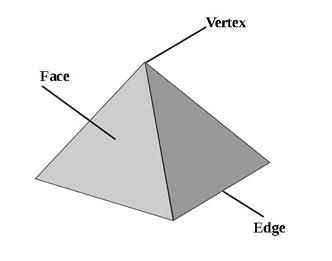
Reference: https://revisionmaths.com/sites/mathsrevision.net/files/imce/3D%20Shapes%20Faces%20Edges%20and%20Vertices%20explained.jpg

Another common mistake is leaving out some when counting. Faces are the most difficult to count since they are so difficult to mark. To help kids count geometric attributes, here are some tips.

Experiencing geometric shapes in physical form gives students real-life experience. As with any other math concept, you must work with concrete materials to gain understanding.
Develop a routine for counting vertices, edges, and faces. Because vertices are the easiest to count and faces are the hardest, it is best that they count attributes in this order: vertices, edges, and faces. Again, let the students practice the routine with physical shapes.
Ask the students to record their counts. Often kids try to hold the numbers in their heads, which does not turn out to be successful.
The V in vertex actually makes a vertex. Edges are simple straight lines, just like capital E. A 3-dimensional shape consists of two-dimensional figures called faces.
The edges are marked with a dash and the vertices are marked with small circles. Teach kids to use an organized approach to counting. To count the vertices below, the square at the bottom has four vertices; mark them first. Ask them to mark the vertex at the top. Likewise, when marking the edges, first mark the four squares on the base, then add the four triangles to the base.
To count faces, they should decompose the figure into its 2-dimensional figures. Here is an example of how it looks. We see 1 square and 4 triangles, so it’s a total of 5 faces.

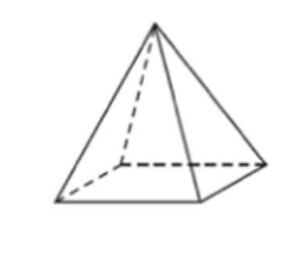
As soon as children can recognize and describe the characteristics that differentiate plane and solid shapes, such as those that make a triangle different from a square or a cylinder different from a cone, they can begin to create and continue patterns. When children create or discover patterns, they use not just one but a number of different attributes to determine the pattern or order.

Using Attribute Block

Attribute blocks are math manipulatives that have four different features. They are a good introduction to logical thinking for young learners. They learn color and shape concepts by sorting blocks.

A block usually consists of four parameters which are shape, size, color, and thickness. Shapes usually include circles, hexagons, squares, rectangles, and triangles. Yellow, red, and blue make up the colors. The two sizes are big and small. There are either thick or thin blocks.

Children should be introduced to one attribute of the blocks at a time. Most recognize the color differences by the time they are in preschool or kindergarten.

Attribute in advanced maths and statistics

In the theory of attributes, qualitative characteristics are calculated through quantitative measurements. Therefore, the attribute requires a slightly different type of statistical treatment than the variables. Attributes refer to the characteristics of the item under study.

In this context, it should be noted that the techniques require statistical knowledge and are applied more widely in the theory of attributes. Since the statistical techniques employ quantitative measurements, qualitative data has to be converted into quantitative data in the theory of attributes.

In the theory of attributes, certain representations are made. In the theory of attributes, the population is divided into two classes, the negative class and the positive class. Positive classes indicate that the attribute is present in the item under study, and they are referred to in the theory of attributes as A, B, C, etc. Negative classes indicate that the attribute is not present in that particular item under study, and is represented as α, β, etc.

Assembling the two attributes, i.e. by combining the letters under consideration (such as AB), denotes the assembling of the two attributes.

Assembling the two attributes is called dichotomous classification. The number of observations that have been assigned to various attributes is known as the class frequency. In this case, the class frequencies are symbolically indicated by bracketing the attribute terms. In this case, (B) represents an attribute class frequency. Frequencies of the class also have some levels in the attribute. The ‘n’ attribute, for example, refers to the class that has the nth order. In the theory of attributes, (B) corresponds to the class of 2nd order.

They also function as operators. By way of example, A.N=(A) indicates the operation of dichotomizing N according to the attribute A gives the class frequency of (A).

In the theory of attributes, there is also an independent nature. Only if the two attributes are completely unrelated can they be considered independent.

A pair of attributes A and B are said to be associated, in the theory of attributes, only if the two attributes are interconnected, but not independent.

Under the following conditions, there is a positive association between the two attributes:

(AB) > (A) (B)/ N.

The negative association between the two attributes exists under the following conditions:

(AB) < (A) (B) /N.

The complete association occurs when the occurrence of attribute A is wholly dependent on the occurrence of attribute B. The same holds true, however, if attribute A is the independent one, then the attribute B may do so without the attribute A.

As a rule, two attributes are said to be associated if they occur together frequently.

The consistency between the two attributes (A)=20 and (AB)=25 is not present as the attribute (AB) cannot be greater than the attribute (A) if they come from the same population.

References

Recommended Worksheets

Defining and Non-defining Attributes of Shapes 1st Grade Math Worksheets
Similar Shapes (Astronomy Themed) Math Worksheets
Comparing Objects Using their Sizes (Sports Themed) Worksheets

Browse All Worksheets

We spend a lot of time researching and compiling the information on this site. If you find this useful in your research, please use the tool below to properly link to or reference Helping with Math as the source. We appreciate your support!