What is an Area?
An object’s area is how much space it occupies in a flat, 2D space. The area is always measured in squares, with square units serving as the unit of area. Area uses the symbol “2“. Thus, areas can be measured in square centimetres (cm2), square feet (ft2), square millimetres (mm2), square metres (m2), square yards (yd2), square kilometres (km2), square feet (ft2), square miles (mi2), and so forth.
For instance, the illustration below shows a rectangle, and we want to measure its area.

One way of doing it is to have several squares that will fill the rectangle’s space. Counting the number of squares used will give us the area.
There is a total of 20 squares used. That is the area of the rectangle.
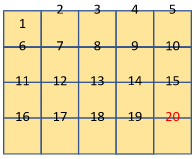
Another way to find the area of the rectangle is to multiply the length and width. We have 4 units x 5 units, which is equal to 20 units.
4 units×5 units=20 unit2
Area Units: Their Relevance
To understand what we are measuring, we utilize units when measuring amounts. Communication is the focus of units. The measuring process involves comparing a known size to a set of standard units. The number has no significance without specifying the reference standards used to compare the unknown.
Let us say, for example, you plan to cover the floor of your room with carpet. You cannot go to the store and tell the staff that you are buying a carpet measuring 10, 20, or 30. You cannot just say any random number, especially without units. Here, it is vital to know the units of measurement so that the staff can assist you and give you the correct item and measure.
Square Unit vs Unit Square
The unit for measuring the area is known as a square unit. A unit square has a side that is one unit long. Square Units and Unit Squares are frequently misunderstood. A unit square, as opposed to a square unit, is a square whose sides are exactly one unit long.
Common Units of Area
Standard International (SI) units of area are measured in square meters. m2 represents a square meter. The square meter may be abbreviated as sq. m. For measuring both big and small areas, units exist. Common units of the area include the following:
Square Millimeter
mm2 for a square millimetre is a square with one millimetre on each side; 1 mm x 1 mm.
Square Centimeter
cm2 for a square centimetre is a square with one centimetre on each side; 1 cm x 1 cm.
Square Decimeter
dm2 for a square decimeter is a square with one decimeter on each side; 1 dm x 1 dm.
Square Meter
m2 for a square meter is a square with one meter on each side; 1 m x 1 m.
Square Yard
yd2 for a square yard is a square with one yard on each side; 1 yd x 1 yd.
Square Inch
in2 for a square inch is a square with one inch on each side; 1 yd x 1 yd.
Square Foot
ft2 for a square foot is a square with one foot on each side; 1 yd x 1 yd.
Square Kilometer
km2 for a square meter is a square with one kilometre on each side; 1 km x 1 km.
Square Mile
mi2 for a square mile is a square with one mile on each side; 1 km x 1 km.
Hectare
The hectare is mainly used to measure land. It is equal to a square with 100-meter sides, or 10,000 m2. One square kilometre equals 100 hectares. Hectare uses the symbol “ha”.
The units for measuring area must be used appropriately depending on the object that needs to be measured. Since we may measure small or big spaces, we must be able to differentiate the units to represent the area.
For small spaces or objects like measurement of the area of a body part, square millimetres can be used. We can use square inches or square centimetres for other objects like books, television, and tables.
For big spaces like the garden lot, living room, bedroom, and basketball court, we can use square meters, square feet, or square yards. For large spaces like the area of a big farm, a town or even a country, square kilometres or miles are used.
Examples
Example 1:
What unit of the area would you use in measuring a single-detached house?
Answer:
The area of a single-detached house is somewhat large, yet there needs to be a suitable unit of measurement. Since square millimetres is a too-small unit, it is not an option. A single-detached house is too small to be measured in hectares. Therefore, the most acceptable unit of area to use when measuring a single-detached house would be square meters.
Example 2:
What unit of the area would you use in measuring England?
Answer:
Since England is a part of the United Kingdom and has a large land area, we must also use a large unit. It must not be possible to use square millimetres, square meters, square inches, or even square yards since they are too small. Therefore, the most acceptable unit of area to use when measuring England would be square kilometres.
Example 3:
What unit of the area would you use in measuring a cellphone?
Answer:
A typical cellphone is a bit smaller than your television or computer screen. Definitely, square meters is not an option since it is a big unit, while square millimetres is a way too small unit. So, square centimetres would be the most appropriate unit of area to measure a cellphone.
Comparing Units of Area
Remember that an object’s area is how much space it occupies in a flat, 2D space.
If the squares below were put side by side, the larger shape would be a rectangle composed of five identical squares.
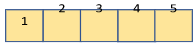
The shaded area below indicates the area of the rectangle, or how much space it takes up.

The area of the yellow square below is 1 square, while the area of the blue rectangle is five squares.

Suppose that each side length of the square is 8 centimetres; when someone asks a question about the size of the square we are using, we can reply that we have a rectangle made up of 5 squares, each of which has a side length of 8 centimetres. To create a rectangle with the same area, we can also use 20 squares, each having a side length of 4 cm.

For direct comparison, it is critical to use the same type of square when comparing areas. Accordingly, whether it is 1 centimetre, 1 meter, 1 foot, 1 yard, 1 inch, or any other 1 unit of length, we are employing a square with a side length of 1.
For example, comparing the rectangles below, the purple rectangle has an area of 16 square centimetres, while the green rectangle has an area of 12 square centimetres. The area of the purple rectangle is greater than the green rectangle.
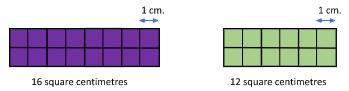
AreaPurple Rectangle>AreaGreen Rectangle
A rectangle’s area can also be calculated by multiplying its length by width. Let us use the image presented above and get its area.
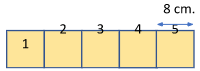
Since each square has a side length of 8 centimetres, we may say that the width of the rectangle is 8 centimetres, and its length is 40 centimetres. The length of 40 centimetres was obtained by multiplying 8 by 5.
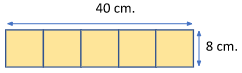
AreaRectangle=40 cm×8 cm
AreaRectangle=320 square centimeter
AreaRectangle=320 cm2
Therefore, the area of the rectangle is 320 square centimetres (320 cm2).
In case you are asked to compare areas with different units, a conversion process can be used. Using their conversion factor, you can change any area unit into any other area unit. The conversion process involves multiplying or dividing the given quantity by a conversion ratio.
Examples
Example 1
Suppose that each side length is 1-inch; compare the area of the figures below.

Solution: Figure A and Figure B are different shapes, and we can compare the area by counting the number of squares each figure has. Since each square has a side length of 1 inch, Figure A has an area of 5 square inches while Figure B has an area of 6 square inches. There is a difference of 1 square inch between their areas. Therefore, the area of Figure B is greater than that of Figure A.
Area (Figure B)>Area (Figure A)
Example 2
Compare the area of the figures below and suppose that each side length is 1 centimetre.
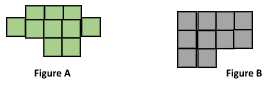
Solution: Let us compare the areas of the given Figures by counting the squares. Figure A has 10 square centimetres, and Figure B also has 10 square centimetres. Therefore, Figure A and Figure B are different in shape, but their areas are the same since they both have 10 square centimetres.
Area (Figure A)=Area (Figure B)
Example 3
Compare the area of the figures below; suppose that each side length measures 1 inch.

Solution: Figure A has 11 square inches while Figure B has 8 square inches. Therefore, Figure A has a greater area than Figure B.
Area (Figure A)>Area (Figure B)
Example 4
Which rectangle has a smaller area?

Solution: Let us use the formula to get the area of a rectangle which is length times width. Since the length of the blue rectangle is 4 centimetres and its width is 3 centimetres, its area is 12 square centimetres. The red rectangle’s length and width are 5 centimetres and 3 centimetres, respectively, and the area is 15 square centimetres.
Area (Blue Rectangle)=4 cm×3 cmArea (Blue Rectangle)=12 cm2
Area (Red Rectangle)=5 cm×3 cmArea (Red Rectangle)=15 cm2
Therefore, the red rectangle’s area is greater than the area of the blue rectangle. The difference between their areas is 3 square centimetres.
Area (Red Rectangle)>Area of Blue Rectangle
Example 5
Which rectangle has the bigger area?

Solution: Let us use the formula to get the area of a rectangle which is length times width. The length of the green rectangle is 5 inches, and its width is 2 inches, so its area is 10 square inches. The length and width of the blue rectangle are 5 inches and 3 inches; respectively, the area is 15 square inches. The red rectangle’s length and width are 6 inches and 3 inches; respectively, the area is 18 square inches.
Area (Green Rectangle) =5 in×2 inArea (Green Rectangle) =10 in2
Area (Blue Rectangle) =5 in×3 inArea (Blue Rectangle) =15 in2
Area (Red Rectangle) =6 in×3 inArea (Red Rectangle) =18 in2
Therefore, among the three rectangles, the red rectangle has the biggest area that, measures 18 square inches.
Conversion Factor: Area Units
Using their conversion factor, you can change any area unit into any other area unit. The tables below show the conversion factors of area units. Since this information is difficult to memorize.




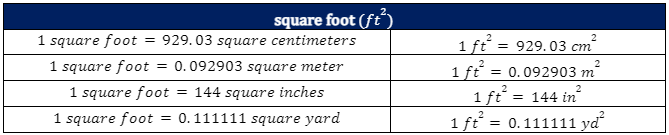
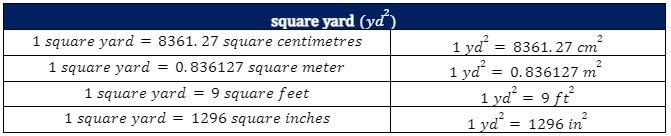



Conversion of Units for Area Measurements
The process of unit conversion involves multiplying or dividing by a numerical factor. Suppose you want to change the units of a measured quantity without changing the value. In that instance, you can convert using a conversion factor representing the relationship between the units. On the other hand, a conversion ratio, if the numerator and denominator have the same value represented in various units, always equals one (1).
Examples
Example 1:
Convert 25000 mm2 to cm2.
Solution:
Let us use the conversion factor, 1 mm2=0.01 cm2.
In this step, we can multiply 25000 mm2 by the conversion ratio $\frac{0.01 cm^2}{1 mm^2}$. Notice that the desired unit is in the numerator of the conversion ratio to cancel the unit of square millimetres.
25000 mm2× $\frac{0.01 cm^2}{1 mm^2}$=250 cm2
Therefore, 25000 mm2 is equal to 250 cm2.
Example 2:
Convert 150 cm2 to m2.
Solution:
Using the conversion factor 1 square meter=10000 square centimetres, we can have the ratio $\frac{1 m^2}{10000 cm^2}$. The desired unit m2 must be the numerator of the conversion ratio.
150 cm2 x $\frac{1 m^2}{10000 cm^2}$=0.015 m2
Thus, 150 cm2 is equal to 0.015 m2.
Example 3:
Convert 200 ft2 to in2.
Solution:
Since the conversion factor of square foot and square inches is 1 square foot=144 square inches, we have $\frac{144 in^2}{1 ft^2}$ as the conversion ratio that we must multiply by 200 ft2.
200 ft2 x $\frac{144 in^2}{1 ft^2}$=28800 in2
Hence, 200 ft2 is equal to 28,000 in2.
Example 4:
Convert 3000 m2 to km2.
Solution:
Let us use the conversion factor, 1 square kilometer=1000000 square meters.
In this step, we can multiply 3000 m2 by the conversion ratio of $\frac{1 km^2}{1000000 m^2}$. Notice that the desired unit is in the numerator of the conversion ratio to cancel the unit of square millimetres.
3000 m2× $\frac{1 km^2}{1000000 m^2}$=0.003 km2
Therefore, 3000 m2 is equal to 0.003 km2.
Example 5:
Convert 5000 cm2 to in2 and m2.
Solution:
- Solution for 5000 cm2 to in2
Since the conversion factor of square centimetres and square inches is 1 square centimeter=0.155 square inches, we have $\frac{0.155 in^2}{1 cm^2}$ as the conversion ratio that we must multiply by 5000 cm2.
5000 cm2 x $\frac{0.155 in^2}{1 cm^2}$=775 in2
Hence, 5000 cm2 is equal to 775 in2.
- Solution for 5000 cm2 to m2
Using the conversion factor 1 square meter=10000 square centimetres, we can have the ratio $\frac{1 m^2}{10000 cm^2}$. The desired unit m2 must be the numerator of the conversion ratio.
5000 cm2 x $\frac{1 m^2}{10000 cm^2}$=0.5 m2
Thus, 5000 cm2 is equal to 0.5 m2.
Example 6:
Find which among the given area is the largest?
0.003 square kilometre
4000 square meters
155000 square inches
1076.39 square feet
Solution: Let us answer this problem by making the given areas with the same units using conversion. Convert the other three units, square kilometres, square inches, and square feet, to square meters. If you want to convert different quantities to square kilometres, square inches, or square feet, you may do so; make sure to use the correct conversion factor.
Conversion of 0.003 square kilometres to square meters
Let us use the conversion factor, 1 square kilometer=1000000 square meters. Then, multiply the given quantity (0.003 km2) by the conversion ratio of $\frac{1000000 m^2}{1 km}$.
0.003 km2 x $\frac{1000000 m^2}{1 km}$=3000 m2
Hence, 0.003 km2 is equal to 3000 m2.
Conversion of 155000 square inches to square meters
Using the conversion factor, 1 square meter=1550 square inches, multiply the given quantity 155000 in2 by the conversion ratio of $\frac{1 m^2}{1550 in^2}$.
155000 in2 x $\frac{1 m^2}{1550 in^2}$=100 m2
Therefore, 155000 in2 is equal to 100 m2.
Conversion of 1076.39 square feet to square meters
Let us use the conversion factor, 1 square foot=0.092903 square meters. And then multiply the given quantity (1096.39 ft2) by the conversion ratio of $\frac{0.092903 m^2}{1 ft^2}$.
1096.39 ft2 x $\frac{0.092903 m^2}{1 ft^2}$≈100 m2
Hence, 1076.39 ft2 is approximately 100 m2.
Since 0.003 km2 equals 3000 m2, 155000 in2 equals 100 m2, and 1076.39 ft2 is approximately 100 m2, the largest area among the given quantities is 4000 square meters.
Summary
- An object’s area is how much space it occupies in a flat, 2D space.
- The area is always measured in squares, with square units serving as the unit of area.
- Communication is the focus of units.
- The unit for measuring the area is known as a square unit.
- A unit square has a side that is one unit long.
- The units for measuring area must be used appropriately depending on the object that needs to be measured. Since we may measure small or big spaces, we must be able to differentiate the units to represent the area.
- Common units of the area include the following:
Square Millimeter ( mm2 )
Square Centimeter ( cm2 )
Square Decimeter ( dm2 )
Square Meter ( m2 )
Square Yard ( yd2 )
Square Inch ( in2 )
Square Foot ( ft2 )
Square Kilometer ( km2 )
Square Mile ( mi2 )
Hectare ( ha ) - The hectare is mainly used to measure land. It is equal to a square with 100-meter sides, or 10,000 m2. One square kilometre equals 100 hectares. Hectare uses the symbol “ha”.
Recommended Worksheets
Measuring Area Using Square Grids (Painting Themed) Worksheets
Spatial Skill: Area (Pearl Harbor Remembrance Day Themed) Math Worksheets
Measurement (Autumnal Equinox Themed) Math Worksheets









