Similar Shapes | Definition, Examples, Scale Factor, Area & Volume

Introduction

Similar shapes are the shapes that have corresponding sides in proportion to every alternative and corresponding angles adequate to each other. Similar shapes look equivalent however the sizes will be different. In general, similar shapes are different from congruent shapes. There are different strategies by that we will notice if two Shapes are similar or not. allow us to learn additional concerning similar shapes and their properties at the side of different resolved examples.

Similar shapes are the shapes that look identical to each other but their sizes may not be precisely the same. Two Figures can be said similar if they need an equivalent form however would possibly be different in size. meaning similar shapes once enlarged or demagnified overlap every other. This property of comparable shapes is spoken as “Similarity” as a whole in the concept of a similar shape.

Definition

Two Shapes mathematically will be considered to be similar shapes :

If they have the identical figure, different sizes with equal corresponding angles congruent, and the length of corresponding sides are in proportion.

Two shapes with the same shape and different sizes are called Similar shapes.

Two shapes will be similar if one shape is an extension of the other shape.

In other words, we can say that, when two shapes are similar then, it means the corresponding sides are in proportion and corresponding angles are equal to each other in given shapes respectively.

When two triangles are similar then their corresponding angles are congruent and the lengths of corresponding sides are in proportion. These triangles are called Similar triangles.

Similarly, when two polygons are similar then their corresponding angles are congruent and the lengths of corresponding sides are in proportion. These polygons are called Similar polygons.

We can generalize this definition of Similar Shapes for that shapes that fulfill the definition of Similar Shapes then these shapes will be similar.

Scale Factor

To understand the concept of the scale factor, we will take two similar shapes, one shape is larger than the other shape then the scale factor will be the ratio of the length of a side of one shape to the length of the corresponding side of the other shape.

Mathematically we will define like, The scale factor of extension is the ratio :

$\frac{Length\: of\: a\: side\: of\: one\: shape}{Length\: of\: the\: corresponding\: side\: of\: the\: other\: shape}$

Example :

The two triangles below are similar. Find the values of X and Y?

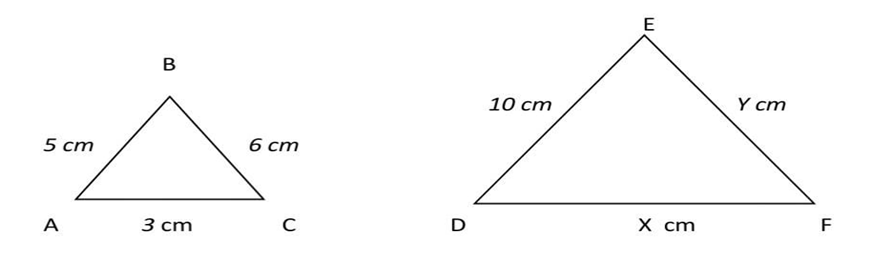
Solution :

The first step is to find the scale factor of the extension. This can be found by dividing the length of two corresponding sides of the given triangles. We can use the length of the two top sides to find the scale factor here.

$\frac{ΔDEF}{ΔABC} = \frac{DE}{AB}$

The scale factor will be :

Scale factor = $\frac{Big}{small} = \frac{DE}{AB}$

= $\frac{10}{5}$

= 2

2 is the scale factor. You can find the value of X and Y by Multiplying 2 With Corresponding Sides Of ΔABC.

3 × 2 = 6 (value of X)

6 × 2 = 12 (value of Y )

Hence, the value of X = 6 and Y = 12 by scale factor = 2.

Alternative Method :

We can find the value of X and Y the similarity of ΔABC and ΔDEF.

To Find the Value Of X,

ΔABC and ΔDEF are similar then the corresponding sides will be equal.

$\frac{DE}{AB}= \frac{EF}{BC} = \frac{DF}{FC}$

$\frac{10}{5} = \frac{X}{3}$

X = $\frac{30}{5}$ = 6

Now to find the value of y, we know that ΔABC and ΔDEF are similar then the corresponding sides will be equal.

$\frac{EF}{BC}= \frac{DE}{AB}$

$\frac{Y}{6} = \frac{10}{5}$

Y = $\frac{60}{5}$ = 12

Hence, the value of X = 6 and Y = 12 by ΔABC ~ ΔDEF.

Some important Steps in Solving Similar Shapes

These are the following steps to solve similar shapes :

Pick out equivalent known values (Lengths, Areas, or Volume)
Make direction ( getting bigger and smaller values)
Determine scale /Area/Volume Factor = Second values ÷First value
Also check Factor > 1 for bigger value and Factor < 1 for smaller value
Use following formulas to find the
Area Factor = (Scale Factor)²
Or Scale Factor = √Area factor
Volume Factor = (Scale Factor)³
Or Scale Factor = ³√Volume factor
By using Scale /Area/Volume Factor to determine the unknown value.

Area of Similar Shapes

We have already read that from the definition of similar shapes if two shapes are similar then their corresponding angles are congruent and the lengths of corresponding sides are in proportion.

For calculating an unknown area in similar shapes, first, we need to calculate the Area Scale Factor for the given similar shapes by dividing the greater length of one shape by the smaller length of another shape.

How to measure

We can measure the area of similar shapes by the area factor formula given by:

Area Factor = (Scale Factor)²

Example :

We have two shapes A and B that are similar shapes. The area of shape B is given which is 330 cm². Find the area of shape A?

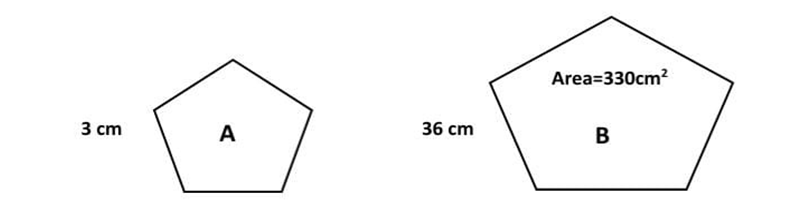
Find the area of shape A?

Solution :

We know that shapes A and B are similar with corresponding sides 3 cm and 36 cm respectively.

Firstly, we will find the scale factor that relates the side-lengths of the shapes dividing the larger by the smaller

Scale factor = $\frac{36}{3}$ = 12

We found the scale factor for the side-lengths which is 12, the scale factor for the areas is given by

Area Factor = (Scale Factor)²

Putting the value of scale factor in above formula,

Area Factor = (12)²

= 144

Therefore, to find the area of the smaller shape, we need to divide the area of the bigger shape by the area scale factor which is 144. After that, we will get

Area of shape A = $\frac{The area of shape B}{Area Factor}$

Area of shape A = $\frac{330}{144}$ = 2.29 cm²

Hence, The area of shape A will be 2.29 cm².

Volume of Similar Shapes

Similarly, for the unknown volume of Similar Shapes, we need to calculate the Volume scale factor for given shapes.

If two shapes are similar with a scale factor of $\frac{X}{Y}$ then volume are in the ratio of ( $\frac{X}{Y}$ )³

How to measure

We can measure the volume of similar shapes by volume factor formula given by:

Volume Factor = (Scale Factor)³

Examples :

We have two cylinder A and B that are similar shapes .The volume of cylinder A is given which is 900 cm³ .Find the volume of cylinder B?

Solution :

We know that cylinder A and B are similar with corresponding length of sides 5 cm and 20 cm respectively.

Firstly, we will find the scale factor that relates the side-lengths of the shapes dividing the larger by the smaller

Scale factor = $\frac{20}{5}$ = 4

We found the scale factor for the side-lengths which is 4, the scale factor for the volume is given by

Volume Factor = (Scale Factor)³

Putting the value of scale factor in above formula,

Volume Factor = (4)³ = 64

We know that volume of cylinder A is 900 cm³ and volume factor = 64, to find the volume of B by volume factor,

Volume of B = volume of cylinder A × volume factor

Volume of B = 900 × 64

= 57600 cm³

Hence, The Volume of Cylinder B will be 57500 cm³.

Solved Examples :

Example 1 :

Two boxes A and B are Mathematically similar.

The total area of box A is 100 cm²

The total area of box B is 2500 cm²

The diameter of box A is 4 cm, Find the diameter of box B?

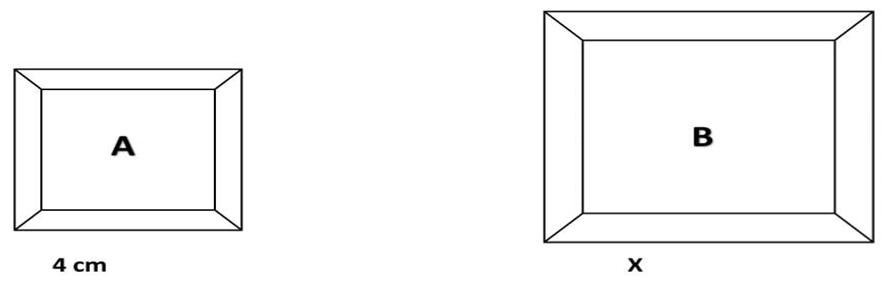
Solution :

We have to find the value of X, For this we know that boxes A and B are similar then by definition of scale factor dividing the large area by smaller area will be,

Area factor = $\frac{2500}{100}$ = 25

Putting the value of area factor in scale factor formula

Scale Factor = √Area factor

Scale Factor = √25

= 5

To find the diameter of box B we will multiply the scale factor with the diameter of box A.

Diameter of box B = 5 × 4 = 20 cm

Hence, the diameter of box B will be 20 cm.

Example 2 :

Below are two similar cones

Cone A has a volume of 25 cm³ with diameter of Cone A is 3 cm and diameter of Cone B is 9 cm.

Find the volume of cone B?

Cone B has a total area of 900 cm²

Find the total area of Cone A?

Solution :

We know that Cone A and Cone B are similar with corresponding diameter 3 cm and 9 cm respectively.

Firstly, we will find the scale factor that relates the diameter of the shapes dividing the larger by the smaller diameters

Scale Factor = $\frac{9}{3}$ = 3

(a) To find the volume of Cone B, we will find the volume factor by following formula

Volume Factor = (Scale Factor)³

Putting the value of scale factor in above formula

Volume Factor = (3)³

Volume Factor = 27

To find the volume of Cone B, we will multiply the volume factor with volume of Cone A

volume of Cone B = Volume Factor × volume of Cone A

= 27 × 25

= 675 cm³

Hence, the volume of Cone B will be 675 cm³.

(b) We already know that the scale factor is 3, To find the total area of Cone A

First we will find the area factor by following formula

Area Factor = (Scale Factor)²

Putting the value of scale factor in above formula

Area Factor = (3)²

Area Factor = 9

For the total area of Cone A, we will divide the area of Cone B by Area Factor

The total area of Cone A = $\frac{Total\:Area\: of\: Cone\: B}{Area\: factor}$

= $\frac{900}{9}$ =100 cm²

Hence, the total area of Cone A will be 100 cm².

Example 3 :

Below are two similar rectangles

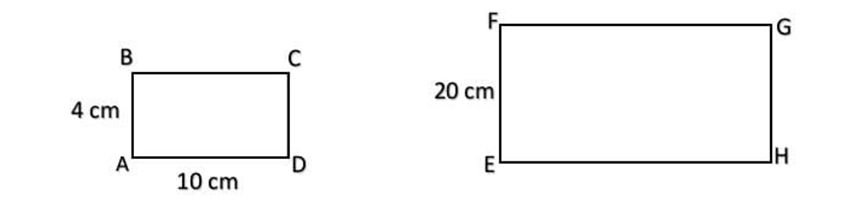
( a ) What is the scale factor from ABCD and EFGH ?

( b ) What is the length of the side EH ?

Solution :

(a) We know that ABCD and EFGH are similar with corresponding length of sides 4 cm and 20 cm respectively.

Firstly, we will find the scale factor that relates the side-lengths of the shapes dividing the larger by the smaller

Scale factor = $\frac{EF}{AB}$

= $\frac{20}{4}$ = 5

Hence, the scale factor from ABCD and EFGH is 5 .

(b) We already find in part (a) the scale factor is 5

To find the value of length of the side EH, we will multiply the corresponding similar shapes length side with scale factor

value of length of the side EH = AD × Scale factor

= 10 × 5 = 50 cm

Hence, the length of the side EH will be 50cm.

Example 4 :

Two shapes given below are similar shapes with different size

The Area of shape B is 360 Cm²

Find the area of shape A?

Solution :

We know that shape A and shape B are similar with corresponding length of sides 2 cm and 12 cm respectively.

Firstly, we will find the scale factor that relates the side-lengths of the shapes dividing the larger by the smaller value.

Scale factor = $\frac{12}{2}$ = 6

The scale factor from A and B is 6 .

Now we will find the area factor by followig formula

Area Factor = (Scale Factor)²

Putting the value of scale factor in above formula

Area Factor = (6)²

Area Factor = 36

To find the area of shape A we will divide area of shape B by area factor.

The area of Shape A = $\frac{Total\: Area\: of\: shape\: B}{Area\: factor}$

$\frac{360}{36}$ = 10 cm²

Hence, the area of shape is 10 cm².

Example 5 :

Below are two similar shapes. Find the value of X.

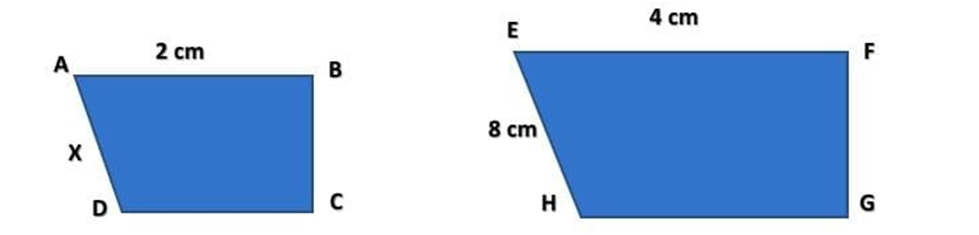
SOLUTION :

We know that both given shapes are similar and AB and EF are the equivalent known lengths with different size.

To find AD we are working from EFGH to ABCD that are similar to each other

so that we are moved towards the value is “getting smaller”

Scale factor = $\frac{AB}{EF} = \frac{2}{4}$ = 0.5 ( Scale factor < 1 )

To find the value of length AD, we will multiply scale factor with the Corresponding length EH of shape EFGH.

X = AD = scale factor × EH

X = AD = 0.5 × 8

X = AD = 4

X = 4 cm

Hence, the length of side AD will be 4 cm.

Example 6 :

Show that the following triangles are similar or not?

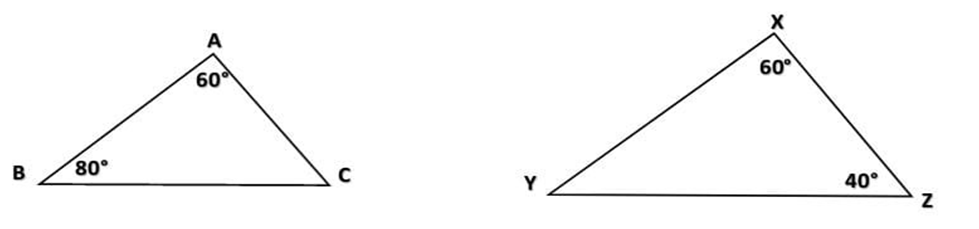
Solution :

We know that sum of interior angles in a triangle = 180°

Therefore, by considering Δ ABC

∠A+ ∠B + ∠C = 180°

60° + 80° + ∠C= 180°

140° + ∠R = 180°

Subtract both sides by 140°.

∠ C= 40°

Consider Δ XYZ

∠X + ∠Y + ∠Z = 180°

∠60° + ∠Y + ∠40°= 180°

∠ 100° + ∠Y = 180 °

Subtract both sides by 100°

∠ Y = 80°

Consider Δ XYZ

∠X + ∠Y + ∠Z = 180°

∠60° + ∠Y + ∠40°= 180°

∠ 100° + ∠Y = 180 °

Subtract both sides by 100°

∠ Y = 80°

Hence;

By Angle-Angle (AA) rule, ΔPQR~ΔXYZ.

∠ B= ∠ Y = 80° and ∠Z = ∠ C= 40°

Since corresponding angles of both triangles are same .

These triangles will be similar to each other.

Example 7 :

Two solids are similar with surface area of the smaller solid (P) is 72π cm²and the surface area of larger solid (Q) is 648π cm². If the height of larger solid is 216 cm then find the height of smaller solid?

Solution :

We know that shape P and shape Q are similar with corresponding Surface Area 72π cm²and 648π cm²respectively.

Firstly, we will find the area scale factor that relates to the surface area of larger solid to the smaller solid.

Area scale factor = $\frac{surface\: area\: of\: larger\: solid}{surface\: area\: of\: smaller\: solid}$

Area scale factor = $\frac{648π cm^2}{72π cm^2}$ = 9 cm²

The area scale factor from P to Q is 9 cm².

Now we will find the scale factor by following formula

Scale Factor = √Area factor

Scale Factor = √9 = 3

To find the height of smaller solid (P) is obtained by dividing the height of larger solide b scale factor

Height of smaller solid (P) = $\frac{The\: height\: of\: larger\: solid}{Scale\: factor}$

= $\frac{216}{3}$ = 72 cm

Hence, the height of smaller solid (P) will be 72 cm .

Example 8 :

The areas of two given below similar shapes are in the ratio of 121 : 225

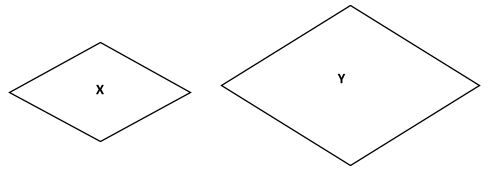
If the length of the shape X is 35.3 cm then find the length of shape Y?

Solution :

Given shapes are similar shapes with ratio

121 :225

Taking square root from both sides of given ratio

11 :15

To find the scale factor we will divide the small ratio vlaue by the length of shape X.

Scale factor = $\frac{Length\: of\: the\: shape\: X}{Small\: ratio\: value}$

Scale factor = $\frac{35.3}{11}$ = 3.2

Now for finding the value of of the length of the shape Y, we will multiply the large ratio value and scale factor

The length of shape Y = scale factor large ratio value in the given ratio

The length of shape Y = 3.2 15

The length of shape Y = 48 cm

Hence, the length of shape Y will be 48 cm .

Key Facts and Summary

Similar shapes have same shape and different sizes,
In similar shapes one shape is an extension of the other shape
The ratio of the length of a side of one shape to the length of the corresponding side of the other Shape is called the scale factor.
Placing bigger and smaller values in order is very important.
While finding the scale factor the vale of nominator value must be greater than denominator value.
With the help of similar shapes, we can find any missing value with corresponding sides of both shapes in which one shape information is given .
We can find Lengths, Areas or Volume in similar shapes from any single value given from three of them.
In similar shapes, scale/Area /volume factors can be calculated from each other by following relations : Area Factor = (Scale Factor)²

Or Scale Factor = √Area factor

Volume Factor = (Scale Factor)³

Or Scale Factor = ³√Volume factor

With the help of similar shapes, we can conclude the whole result for similar shape by solving on of them with the help of scale factor.

Recommended Worksheets

Browse All Worksheets

We spend a lot of time researching and compiling the information on this site. If you find this useful in your research, please use the tool below to properly link to or reference Helping with Math as the source. We appreciate your support!