Similarity/Alike is a genre studied in mathematics that is very well known. It is frequently depicted as a problem in figures. In similarity problems, there are proof and calculation problems. Therefore, it is essential that young learners understand the conditions under which figures are similar. Furthermore, they should be able to figure out the side lengths of similar figures. In this case, proportional expressions are used.
What is Similarity?
When two or more figures or objects appear to be the same or equal when it comes to their shape, it is known as similarity (being alike). Similarity is an enlargement or reduction of objects. For example, a picture can be enlarged or reduced in two ways. One way is to stretch/shrink it in proportion, and the other is to stretch/shrink it horizontally or vertically. An enlargement/ reduction by proportion means that if we want to increase/decrease the length by a certain percentage, we must also increase/decrease the width by the same percentage.
Similar figures always superimpose each other when magnified or demagnified. To be more precise, one can be obtained from the other through uniform scaling (enlarging or reducing), possibly with additional translation, rotation, and reflection. As a result, either image can be resized, repositioned, and reflected, so that it coincides perfectly with the other image. Objects that are similar are congruent with each other when a uniform scaling has been applied. For example, all circles are similar to one another, all squares are similar to one another, and all equilateral triangles are similar to one another. Similarly, ellipses are not all alike, rectangles are not all alike, and isosceles triangles are not all alike.
All geometric figures that have the same shape but different sizes are known as similar figures. In general, any two line segments will always be similar, but they do not need to be congruent. If their lengths are equal, they are congruent.
Mathematically, two figures are similar if their corresponding angles are congruent (congruent angles have the same measure) and the ratios of the lengths of their corresponding sides are equal. We call this common ratio a scale factor. The symbol ∼ is used to indicate similarity.
What are similar Shapes?
Euclidean geometry defines similar objects as those that have the same shape, or as those whose mirror image is similar. To put it more precisely, using uniform scaling (enlarging or reducing) and possibly rotation, translation, and reflection, one can be obtained from the other. This means that either object can be scaled, positioned, and mirrored, so as to intersect exactly with the other. Similar objects are congruent when the results of a uniform scaling are the same.
- If one shape is an enlargement of another, then mathematically they are similar
- Equivalent angles in the two shapes will be equal
- The equivalent lengths in the two shapes will be in the same ratio and linked by a scale factor (which you will normally have to calculate).
Working with similar shapes
- Determine equivalent known lengths
- Establish a direction (getting bigger or smaller?)
- Find scale factor = Second Length ÷ First Length
- (Check that SF < 1 is getting smaller and SF > 1 is getting bigger )
- The scale factor is used to find the length
Example
In the figure below, pentagon ABCDE ∼ pentagon VWXYZ
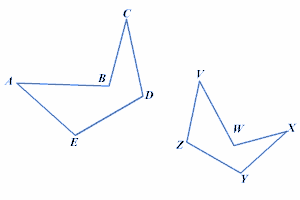
Two-dimensional figures are similar if the second can be obtained from the first through rotations, reflections, translations, and dilations.
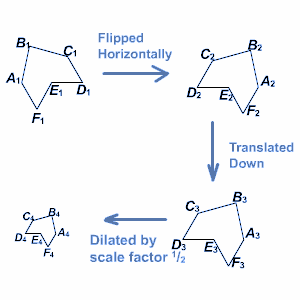
In the given figure above,
- The hexagon A1B1C1D1E1F1 is horizontally flipped to get A2B2C2D2E2F2
- Then the hexagon A2B2C2D2E2F2 is translated to get A3B3C3D3E3F3
- Finally, the Hexagon A3B3C3D3E3F3 is dilated by a scale factor of ½ to get A4B4C4D4E4F4
Here note that A1B1C1D1E1F1 ∼ A2B2C2D2E2F2 ∼ A3B3C3D3E3F3 ∼ A4B4C4D4E4F4
That is, all four hexagons are similar. In fact, based on the figure the first three are congruent.
Rules of Similarity
When two linear figures are similar, it means:
- All the corresponding angle pairs are equal.
- All the corresponding sides are proportional.
Similar Polygons
In mathematics, two polygons having the same number of sides are called similar. This occurs if:
1. The corresponding angles are equal, and
2. The lengths of their corresponding sides are proportional
If two polygons ABCDE and PQRST are similar, they can be written as ABCDE∼PQRST, where the symbol stands for ‘is similar to.’
From the above definition, it follows that:
- The angle at A = The angle at P
- The angle at B = The angle at Q,
- The angle at C = The angle at R,
- The angle at D = The angle at S,
- The angle at E = The angle at T.
Therefore we can conclude, AB/PQ = BC/QR = CD/RS = DE/ST = EA/TP
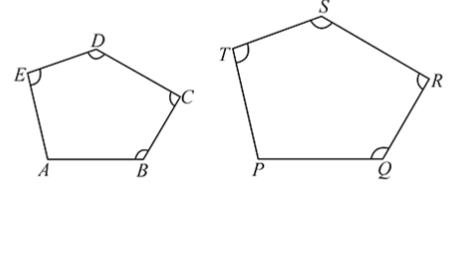
When it comes to polygons with more than three sides, the two conditions given in the definition are not independent of each other, i.e., any one of the two conditions without the other is not sufficient for polygons with more than three sides to be similar. In other words, the two polygons need not be similar if the angles of the corresponding sides of both polygons are the same but their lengths are not proportional. The same argument applies if the corresponding angles of two polygons do not match up but their sides are proportional.
We can say a triangle is a special type of polygon. If either of the two conditions given above holds, then the other holds automatically in triangles.
Similar Triangles
Listed here are some of the properties of similar triangles
- Both have the same shape, but sizes may differ
- Each pair of corresponding angles are equal
- The ratio between the corresponding sides is the same
Using triangle rules is essential when we do not know all angles and sides of two triangles.
There are a few ways to prove similarity. The methods are similar to those used to prove congruence–they prove all corresponding angles are congruent and all corresponding sides are proportional without needing to know the measurements of all six parts of each triangle.
AA similarity criterion
A triangle is similar if its angles are equal to those of another. According to the AA criterion for triangle similarity, two triangles are similar if their angles are identical. Equiangular triangles, therefore, have similar angles.
In theory, this criterion should be named AAA (Angle-Angle-Angle) criterion, but we call it AA since two angles must be equal for the third pair to also be equal due to the angle sum property of triangles.
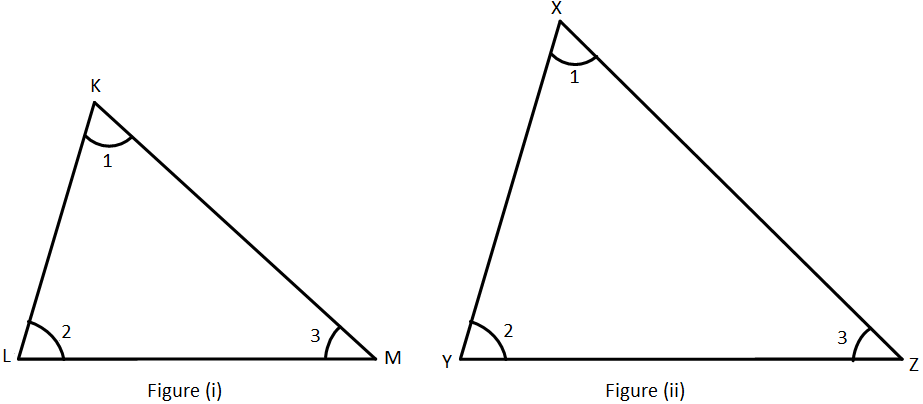
Here is an example in which ΔKLM and ΔXYZ are equiangular, i.e.,
∠K = ∠X
∠L = ∠Y
∠M = ∠Z
Reference: https://www.math-only-math.com/images/side-angle-side-congruency.png
These triangles are said to be similar based on the AA criterion.
SSS similarity criterion
The SSS similarity criterion states that two triangles are similar if their three sides are proportional to each other.
In other words, the triangles in such pairs will be identical (each corresponding pair of angles is the same).
Here’s an example, where two triangles are proportional to one another (ΔKLM and ΔXYZ):
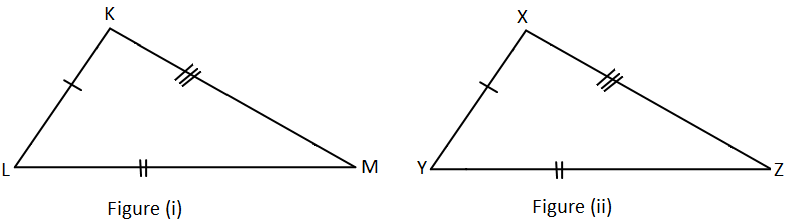
Reference: https://www.math-only-math.com/images/side-side-side-congruency.png
KL = XY, LM = YZ and KM = XZ.
Therefore, ∆KLM ≅ ∆XYZ.
SAS similarity criterion
The SAS similarity criterion states that if two sides of one triangle are proportional to two sides of another, and if the included angles are equal, then the two triangles are similar.
There is a strong emphasis on the word included. Then the two triangles may not be similar if the equal angle is a non-included angle.
Consider the following figure:
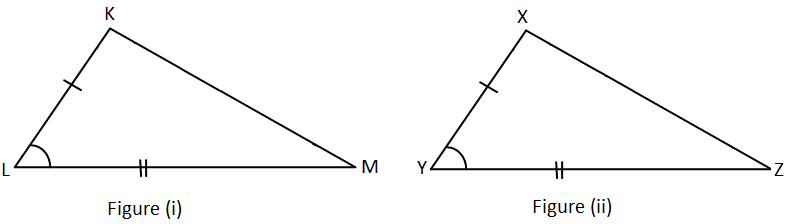
Reference: https://www.math-only-math.com/images/side-angle-side-congruency.png
Here in ∆KLM and ∆XYZ,
KL = XY, LM = YZ and ∠L = ∠Y
Therefore, ∆KLM ≅ ∆XYZ.
RHS similarity criterion
The two triangles are similar if the ratio of the hypotenuse and one side of a right-angled triangle is equal to the ratio of the hypotenuse and one side of another right-angled triangle.

In the figure, ∠L = ∠Y = 90°, KM = XZ and KL = XY.
Therefore, ∆KLM ≅ ∆XYZ
In Euclidean geometry, there are several elementary results concerning similar triangles:
- Any two equilateral triangles are similar.
- Two triangles are similar to each other (transitivity of similarity of triangles) and both are similar to a third triangle.
- In similar triangles, the corresponding altitudes have the same ratio as the corresponding sides.
- Two right triangles are similar if their hypotenuse and one other side have the same ratio of lengths. In this case, there are several equivalent conditions such as the right triangles having an acute angle of the same measure, or having the lengths of the sides being in the same proportion.
Examples of similarity/alike
Q1: Consider the following figure:
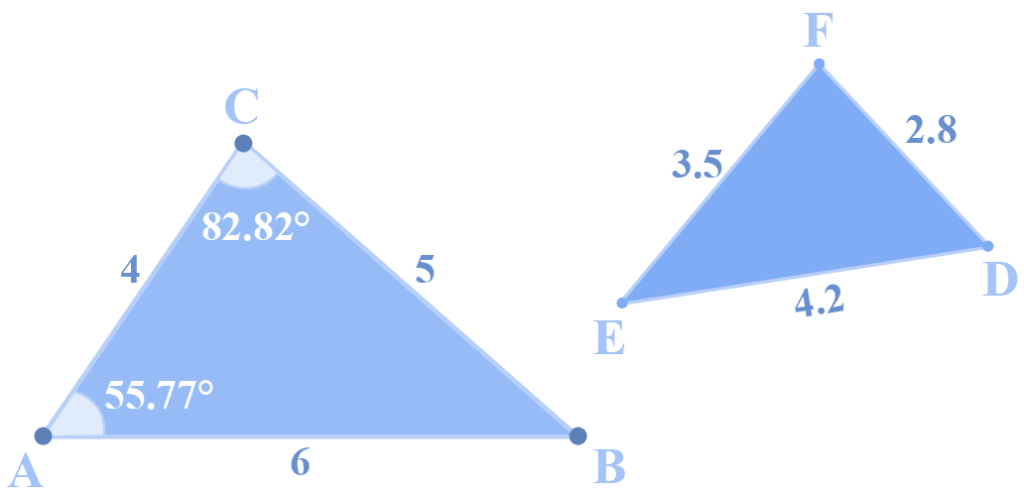
Find the value of ∠E.
Solution
Make sure that the longest side matches the longest side and the shortest side matches the shortest side and compare all three ratios.
Each of the two triangles has three sides that are proportional:
DE/AB = 4.2/6 = 0.7
DF/AC = 2.8/4 = 0.7
EF/BC = 3.5/5 = 0.7
DE/AB = DF/AC = EF/BC
Thus, by SAS similarity criterion, ΔABC∼ΔDEF. This means that they are also equiangular.
Note carefully that the equal angles will be:
∠A = ∠D = 55.770
∠C = ∠F = 82.820
∠B = ∠E
Finally, ∠E = ∠B = 1800 − (55.770 + 82.820) ⇒ ∠E = 41.410
∠E = ∠B = 180 − (55.770 + 82.820)
⇒∠E = 41.410
Hence AD = 8cm
Q2: Consider two similar triangles, ΔABC and ΔDEF. AP and DQ are medians in the two triangles respectively. Show that AP/BC=DQ/EF
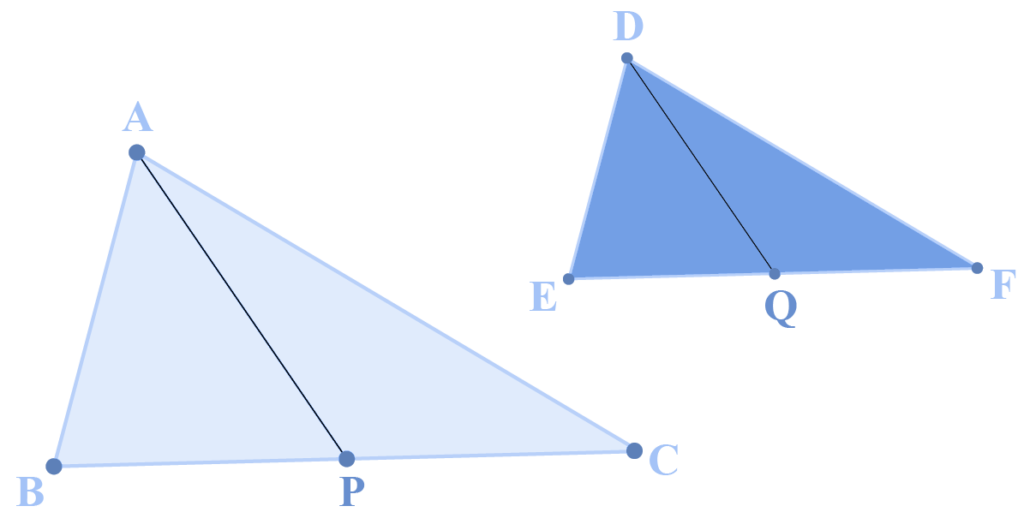
Solution
Since the two triangles are similar, they are equiangular.
This means that, ∠B=∠E
Also, AB/DE = BC/EF ⇒ AB/DE = (BC/2) / (EF/2) = BP/EQ
Hence, by the SAS similarity criterion,
ΔABP∼ΔDEQ
Thus, the sides of these two triangles will be respectively proportional, and so:
AB/DE = AP/DQ ⇒ AP/DQ = BC/EF ⇒ AP/BC = DQ/EF
Q3: In the ΔABC length of the sides is given as AP = 5 cm, PB = 10 cm and BC = 20 cm. Also PQ||BC. Find PQ.
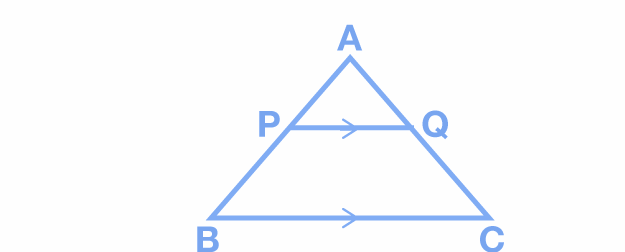
Solution
In ΔABC and ΔAPQ, ∠PAQ is common and ∠APQ = ∠ABC (corresponding angles)
⇒ ΔABC ~ ΔAPQ (AA criterion for similar triangles)
⇒ AP/AB = PQ/BC
⇒ 5/15 = PQ/20
⇒ PQ = 20/3 cm
Q4: Check if the two triangles are similar.

Solution
In triangle PQR, by angle sum property;
∠P + ∠Q + ∠R = 180°
60° + 70° + ∠R = 180°
130° + ∠R = 180°
Subtract both sides by 130°.
∠ R= 50°
Again in triangle XYZ, by angle sum property;
∠X + ∠Y + ∠Z = 180°
∠60° + ∠Y + ∠50°= 180°
∠ 110° + ∠Y = 180 °
Subtract both sides by 110°
∠ Y = 70°
Since,∠Q = ∠ Y = 70° and ∠Z = ∠ R= 50°
Therefore, by the Angle-Angle (AA) rule,
ΔPQR~ΔXYZ
Difference Between Similarity and Congruency?
A pair of identical figures are congruent if they have the same size and shape. They are similar if they have the same shape, but not the same size.
A congruent figure is equal in all aspects, which means that its perimeter, its length, and its area are all equal.
The key difference is all congruent figures are similar but similar figures are not congruent.
Similar Triangles and Congruent Triangles
In the table below, we share a few comparisons between similar triangles and congruent triangles
| Similar Triangles | Congruent Triangles |
| They are the same shape but different in size | They are the same in shape and size |
| The symbol used is ‘~’ | The symbol used in this case ‘≅’ |
| The ratio of all the corresponding sides is the same. | The ratio of corresponding sides is equal to a constant value |
Similarity as a Size Transformation
As already mentioned earlier, if two figures have the same shape but differ in size, they are said to be similar. A rigid motion combined with rescaling is known as a similarity transformation. Another way of looking at it is that a similarity transformation can change the location and size while preserving the shape.
Scaled Drawing
A scaled drawing of an object has the same shape as the object, but its size is different.
The drawing scale is determined by the ratio between the length of the drawing and the actual thing.
There are two ways to write a scale: a size ratio or a number-to-length ratio.
Imagine the following scales: 1:400 and 11 centimeters: 4 meters
A scale equals the ratio of matching lengths, and the matching angles are equal.
Types of Similarity Transformation
There are four main types of similarity transformations. These are outlined below.
- Reflection – Mirror images can be created by flipping shapes across an imaginary line.
- Rotation – To rotate or turn shapes, an axis is used.
- Translation – Sliding shapes across the plane
- Dilation – Increasing or decreasing the dimensions of an object or shape to make it larger or smaller
Reflection
In geometry, a flip represents a reflection. Mirror images of shapes are known as reflections. A line of reflection represents an image reflecting itself. When a figure is described as a mirror image of another figure, then each point in the first figure is equidistant from the corresponding point in the second figure. Reflected images should have the same size and shape as the original, but should be facing the opposite way.
Rotation
In order to determine whether the triangles are identical, we must arrange them in the same orientation. To accomplish this, one shape needs to be rotated to match the other. Rotation is the term for such a transformation.
Translation
By seeing a polygon and its translation, you might think the same polygon is being shown twice. We translate shapes by sliding them on the plane they exist in without changing their orientation (we do not rotate them).
Dilation or Resize
A dilation is a transformation that is used to resize an object. A dilation makes items appear larger or smaller. This transformation produces the same image as the original. However, there is a size difference in the shape. Dilation can be used to expand or reduce the original shape. The term “scale factor” defines this transformation.
Similarity in Polygons
The concept of similarity is applicable to polygons with more than three sides. A pair of similar polygons are equivalent if the corresponding sides are taken in the same sequence (even if the sequence is counterclockwise for one polygon and clockwise for another). Nevertheless, the proportionality of corresponding sides alone does not prove similarity for polygons beyond triangles (otherwise, all rhombic polygons would be similar). In the same way, the equality of all angles in sequence does not guarantee similarity (otherwise, all rectangles would be the same). In order for polygons to be similar, their corresponding sides and diagonals must be proportional.
Application of Similarity?
Here are a few examples of how similarity can be applied.
- The concept of similarity is widely used in architecture.
- Problems are solved by using height and distance.
- Using triangles to solve mathematical problems.
Conclusion
To conclude here are a few observations. Separate out the common formula from particular instances of a shape. All circles are similar, but a bigger circle is better than a small one.
Analogies help us remember. Similarity goes beyond geometry – it’s about identifying classes of items that have the same internal properties.
The real definition of similarity is much more nuanced: they can be said to be similar if formulas based on their distance are always the same (e.g. to be uniformly scaled or dilated).
Reference:
- https://www.math-only-math.com/criteria-for-congruency.html
- https://byjus.com/maths/similar-triangles/
- http://www.differencebetween.net/language/difference-between-congruent-and-similarity/
- https://www.toppr.com/guides/maths/triangles/similarity-of-triangles/
Recommended Worksheets
Understanding Congruence and Similarity of 2D Figures 8th Grade Math Worksheets
Triangles (Fashion Themed) Worksheets
Identifying Triangles, Quadrilaterals, Pentagons, Hexagons, and Cubes 2nd Grade Math Worksheets









