Hyperbola | Definition, Examples, Equation In Standard Form, Properties

Introduction

A conic section as the name implies is a section cut off from a circular ( not necessarily a right circular ) cone by a plane in various ways. The shape of the section depends upon the position of the cutting plane. In other words conic section or conic is the locus of a point P which moves in such a way that its distance from a fixed point S always bears a constant ratio to its distance from a fixed line, all being in the same plane.

One such important conic is the hyperbola. Let us learn more about it.

Definition

A hyperbola is a type of conic section formed by the intersection of the double cone by a plane surface, but not necessarily at the centre. Mathematically, a hyperbola is the locus of a point in a plane which moves in the plane in such a way that the ratio of its distance from a fixed point ( called the focus ) in the same plane to its distance from a fixed line ( called directrix ) is always constant which is always greater than unity. The constant ratio is generally denoted by e and is known as the eccentricity of the hyperbola.

So, if S is the focus and P is any point on the hyperbola, then by definition,

$\frac{SP}{PM}$ = e ⇒ SP = e . PM

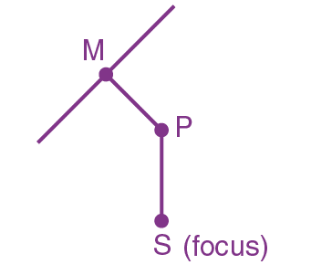
Let us understand it through an example.

Example

Find the equation of the hyperbola whsoe focus is ( 1 , 2 ), directrix the line x + y + 1 = 0 and eccentricity 3 / 2.

Solution

Let S ( 1 , 2 ) be the focus and let P ( x , y ) be a point on the hyperbola. If we have a perpendicular PM from P on the directrix x + y + 1 = 0, then,

SP = e . PM . . . . . . . . . . . . . . . . . . ( by definition )

⇒ $\sqrt{( x-1 )^2+ ( y-2 )^2} = \frac{3}{2} \left|\frac{x+y+1}{\sqrt{1^2+ 1^2}} \right|$

⇒ ( x-1 )² + ( y-2 )² = $\frac{9}{4}\left | \frac{( x+y+1 )^2}{2}\right |$

⇒ 8 [( x-1 )² + ( y-2 )² ]= 9 (x + y +1)²

⇒ 8 x² + 8 y² – 16 x – 32 y + 40 = 9 x² + 9 y² + 9 + 18 x y + 18 x + 18 y

⇒ x² + 9y² + 18 x y + 34 x + 50 y – 31 = 0 is the required equation of the hyperbola.

Equation of the Hyperbola in Standard Form

Let S be the focus, ZK be the directrix and e be the eccentricity of the hyperbola whose equation is required. Let us draw SK perpendicular from S on the directrix ZK and divide SK internally and externally at A and A ‘ ( on SK produced ) respectively in the ratio e : 1.

Then, S A = e A K . . . . . . . . . . . . . . . . . . . ( 1 ) and

S A ‘ = e A ‘ K ‘ . . . . . . . . . . . . . . . . . . . . . . . . .. ( 2 )

Since, A and A ‘ are such points that their distances from the focus bear constant ratio e ( > 1 ) to their respective distances from the directrix. Therefore, these points lie on the hyperbola.

Let A A ‘ = 2 a and C be the middle point of A A ‘. Then, C A = C A ‘ = a

Adding equation ( 1 ) and equation ( 2 ) we get,

S A + S A ‘ = e ( A K + A K ‘ )

⇒ C S – C A + C S + C A ‘ = e ( C A – C K + C A ‘ + C K )

⇒ 2 C S = 2 a c

⇒ C S = a e

Subtracting equation ( 1 ) from equation ( 2 )

S A ‘ – S A = e ( A ‘ K – A K )

⇒ ( C S ‘ + S A ‘ ) – ( C S + C A ) = e ( C A ‘ + C K – C A + C K )

⇒ A A ‘ = 2 e ( C K )

⇒ 2 a = 2 e ( C K )

⇒ C K = $\frac{a}{e}$

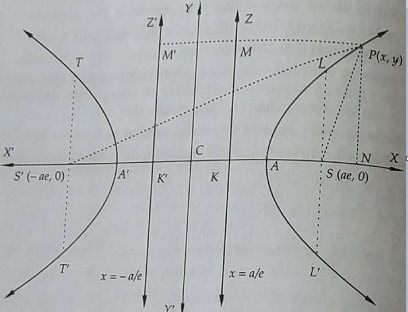
Let C be the origin C S X the axis of x and a straight line C Y through C perpendicular to C X as the axis of Y. Let P ( x , y ) be any point on the hyperbola and P M, P N be the perpendicular from P on K Z and K X. by definition of hyperbola,

S P = e P M

⇒ S P ² = e ² P M ²

⇒ S P ² = e ² K N ²

⇒ S P ² = e ² ( C N – C K ) ²

⇒ ( x – a e ) ² + y ² = e ² ( x – $\frac{a}{e}$ ) ²

⇒ x ² ( e ² – 1 ) – y ² = a ² ( e ² – 1 )

⇒ $\frac{x^2}{a^2} -( \frac{y^2}{a^2 ( e^2-1 )})$ = 1

⇒ $\frac{x^2}{a^2} – \frac{y^2}{b^2}$ = 1 where b ² = a ² ( e ² – 1 )

This is the equation of the hyperbola in standard form.

Hence, if P ( x , y ) be any point on the hyperbola, then the standard equation of the hyperbolas is given by $\frac{x^2}{a^2} – \frac{y^2}{b^2}$ = 1 where b ² = a ² ( e ² – 1 )

Various Elements of a Hyperbola

Let us now learn about various elements of a hyperbola. For a hyperbola, $\frac{x^2}{a^2} – \frac{y^2}{b^2}$ = 1, we have the following elements –

Vertices –The points where the hyperbola intersects the axis are called the vertices. Hence, the points A and A ‘ that we discussed in the above figure, where the curve meets the line joining the foci S and S ‘ are called the vertices of a hyperbola. The coordinates of A and A ‘ are ( a , 0 ) and ( ( – a , 0 ) respectively.

Transverse and Conjugate Axis – The line passing through the two foci and the centre of the hyperbola is called the transverse axis of the hyperbola. The straight line joining the vertices A and A ‘ is called the transverse axis of the hyperbola. Its length A A ‘ is generally taken to be 2 a. The line passing through the centre of the hyperbola and perpendicular to the transverse axis is called the conjugate axis of the hyperbola. The straight line through the centre which is perpendicular to the transverse axis does not meet the hyperbola in real points. But if B, B ‘ be the points on this line such that C B = C B ‘ = b, the line B B ‘ is called the conjugate axis such that B B ‘ = 2 b.

Foci – The points S ( a e , 0 ) and S ‘ ( – a e , 0 ) are the foci of the hyperbola.

Directrices – Z K and Z K ‘ are two directrices of the hyperbola and their equations are x = $\frac{a}{e}$ and x = – $\frac{a}{e}$ respectively.

Centre – The midpoint of the line joining the two foci is called the centre of the hyperbola. Hence, the middle point C of A A ‘bisects every chord of the hyperbola passing through it and is called the centre of the hyperbola.

Eccentricity – The eccentricity is the ratio of the distance of the focus from the centre of the hyperbola, and the distance of the vertex from the centre of the hyperbola. The distance of the focus is ‘c’ units, and the distance of the vertex is ‘a’ units, and hence the eccentricity is e = c/a. Hence, for the hyperbola, \frac{x^2}{a^2} – \frac{y^2}{b^2} = 1, we have

b ² = a ² ( e ² – 1 )

⇒ e ² = $\frac{a^2 + b^2}{a^2}$ = 1 + $\frac{b^2}{a^2}$

⇒ e = $\sqrt{1 + \frac{b^2}{a^2}} = \sqrt{1 + \frac{( 2b )^2}{(2a)^2}}$

⇒ e = $\sqrt{1+\frac{(conjugate\: axis)^2}{( transverse\: axis )^2}}$

Length of Latus rectum – The latus rectum is a line drawn perpendicular to the transverse axis of the hyperbola and is passing through the foci of the hyperbola. The length of the latus rectum of the hyperbola is 2 b ²/a. for further understanding of the latus rectum, let L S L ‘ be the latus rectum, then L S is called the semi latus rectum. It is important to understand here that T S ‘ T ‘ is also a latus rectum. Now,

The coordinates of L are ( a e , S L ). As L lies on the hyperbola, $\frac{x^2}{a^2} – \frac{y^2}{b^2}$ = 1, the coordinates of L will satisfy the equation of the hyperbola. This means that

$\frac{x^2}{a^2} – \frac{y^2}{b^2}$ = 1

⇒ $\frac{( ae )^2}{a^2} – \frac{( SL )^2}{b^2}$ = 1

⇒ ( S L ) ² = b ² ( e ² – 1 )

⇒ ( S L ) ² = $\frac{b^2}{a}$

Therefore, S L = S L ‘ = $\frac{b^2}{a}$

Properties of a Hyperbola

The following are the properties of a Hyperbola –

Asymptotes

The pair of straight lines are drawn parallel to the hyperbola and are assumed to touch the hyperbola at infinity. The equations of the asymptotes of the hyperbola are y = b x / a, and y = – b x / a respectively.

Rectangular Hyperbola

The hyperbola having the transverse axis and the conjugate axis of the same length is called the rectangular hyperbola.

Direction Circle

The locus of the point of intersection of perpendicular tangents to the hyperbola is called the director circle.

Auxillary Circle

A circle drawn with the endpoints of the transverse axis of the hyperbola as its diameter is called the auxiliary circle.

Solved Examples

Example 1 For the given equation, find the length of the transverse and conjugate axis, eccentricity and coordinates of foci and vertices, length of the latus rectum and equation of directrices

16 x ² – 9 y ² = 144

Solution We have been given the equation 16 x ² – 9 y ² = 144 and we are required to find the length of the transverse and conjugate axis, eccentricity and coordinates of foci and vertices, length of the latus rectum and equation of directrices. Let us find each one of these one by one.

The equation 16 x ² – 9 y ² = 144 can be written as $\frac{x^2}{9} – \frac{y^2}{16}$ = 1

This is of the form $\frac{x^2}{a^2} – \frac{y^2}{b^2}$ = 1, where a ² = 9 and b ² = 16

Length of the transverse axis – The length of the transverse axis = 2 a = 2 x 3 = 6

Length of the conjugate axis – The length of the conjugate axis = 2 b = 2 x 4 = 8

Eccentricity – We know that the eccentricity is given by e = $\sqrt{1 + \frac{b^2}{a^2}}$

⇒ e = $\sqrt{1 + \frac{16}{9}}$ = 53

Foci The coordinates of the foci are ( ± a e , 0 ) i.e. ( ± 5 , 0 )

Vertices – The coordinates of the vertices are ( ± a , 0 ) i.e. ( ± 3 , 0 )

Latus rectum – The length of the latus rectum = 2 b ²/a = 32 / 3

Equation of the directrix – The equations of the directrices are x = ± $\frac{a}{e}$, i.e. x = ±$\frac{9}{5}$

Example 2 Find the equation of the hyperbola whose conjugate axis is 5 and the distance between the foci is 13

Solution Let 2 a and 2 b be the transverse and conjugate axes and e be the eccentricity. Let the centre be the origin and the transverse and the conjugate axes the coordinate axes. Then, the equation of the hyperbola is $\frac{x^2}{a^2} – \frac{y^2}{b^2}$ = 1 . . . . . . . . . . . . . . . . . . . . ( 1 )

Now, we have, 2 b = 5 and 2 a e = 13

Also, b ² = a ² ( e ² – 1 )

⇒ b ² = a ² e ² – a ²

⇒ $\frac{25}{4} = \frac{169}{4}$ – a ²

⇒ a ² = $\frac{144}{4}$

⇒ a = 6

Substituting the value of a and b in equation ( 1 ), the equation of the hyperbola, we will have,

$\frac{x^2}{36} – \frac{y^2}{25/4}$ = 1

25 x ² – 144 y ² = 900

Hence, the equation of the hyperbola whose conjugate axis is 5 and the distance between the foci is 13 will be 25 x ² – 144 y ² = 900

Key Facts and Summary

A hyperbola is the locus of a point in a plane that moves in the plane in such a way that the ratio of its distance from a fixed point ( called the focus ) in the same plane to its distance from a fixed line ( called directrix ) is always constant which is always greater than unity.
The constant ratio is generally denoted by e and is known as the eccentricity of the hyperbola.
If P ( x , y ) be any point on the hyperbola, then the standard equation of the hyperbolas is given by \frac{x^2}{a^2} – \frac{y^2}{b^2} = 1 where b ² = a ² ( e ² – 1 )
The points where the hyperbola intersects the axis are called the vertices. Hence, the points A and A ‘ that we discussed in the above figure, where the curve meets the line joining the foci S and S ‘ are called the vertices of a hyperbola. The coordinates of A and A ‘ are ( a , 0 ) and ( ( – a , 0 ) respectively.
The line passing through the two foci and the centre of the hyperbola is called the transverse axis of the hyperbola. The straight line joining the vertices A and A ‘ is called the transverse axis of the hyperbola. Its length A A ‘ is generally taken to be 2 a.
The line passing through the centre of the hyperbola and perpendicular to the transverse axis is called the conjugate axis of the hyperbola. The straight line through the centre which is perpendicular to the transverse axis does not meet the hyperbola in real points. But if B, B ‘ be the points on this line such that C B = C B ‘ = b, the line B B ‘ is called the conjugate axis such that B B ‘ = 2 b.
The points S ( a e , 0 ) and S ‘ ( – a e , 0 ) are the foci of the hyperbola.
Z K and Z K ‘ are two directrices of the hyperbola and their equations are x = $\frac{a}{e}$ and x = – $\frac{a}{e}$ respectively.
The midpoint of the line joining the two foci is called the centre of the hyperbola. Hence, the middle point C of A A ‘bisects every chord of the hyperbola passing through it and is called the centre of the hyperbola.
The eccentricity is the ratio of the distance of the focus from the centre of the hyperbola, and the distance of the vertex from the centre of the hyperbola. The distance of the focus is ‘c’ units, and the distance of the vertex is ‘a’ units, and hence the eccentricity is e = c/a.
The line passing through the centre of the hyperbola and perpendicular to the transverse axis is called the conjugate axis of the hyperbola.
The pair of straight lines are drawn parallel to the hyperbola and are assumed to touch the hyperbola at infinity. The equations of the asymptotes of the hyperbola are y = b x / a, and y = – b x / a respectively.
The hyperbola having the transverse axis and the conjugate axis of the same length is called the rectangular hyperbola.
The locus of the point of intersection of perpendicular tangents to the hyperbola is called the director circle.
A circle drawn with the endpoints of the transverse axis of the hyperbola as its diameter is called the auxiliary circle.

Recommended Worksheets

Line Graphs (International Nurses Day Themed) Math Worksheets
Spatial Skill: Circles (New Year’s Eve Themed) Math Worksheets

Browse All Worksheets

We spend a lot of time researching and compiling the information on this site. If you find this useful in your research, please use the tool below to properly link to or reference Helping with Math as the source. We appreciate your support!