The Idea of Space
When we look at something empty, like a box, room or bowl, even though it seems empty, it still has space. We can keep things in that space. For example, a park has space for us to play. The things we are talking about such as the room, the bowl, the box are all solid in shape. We read about solids, liquids and gases in science. So, what are solids in mathematics? Let us find out
Solid
The definition of a solid is no different from what we learn in science. An object that has a fixed shape and size is called a solid. Some properties of a solid are:
- A solid occupies a fixed amount of space.
- Solid occur in different shapes and sizes.
These solid shapes are known as 3-dimensional shapes. Why do we call them 3-dimensional? To understand this, we first need to understand what we mean by the word 3-dimensional shapes.
3D Shapes
3 Dimensional shapes or 3D shapes are the shapes that have all the three dimensions, i.e. length, breadth and height. These shapes are called solid shapes. In our everyday lives, we come across many solid shapes. For example, the laptop, our rooms, mobile phones, ice cream, tennis balls etc. are all examples of solid shapes. Let us understand some of these shapes in detail. But, before we look at the different solid shapes, we need to understand some common terms that are used to define different dimensions of solid shapes. So, here we have to define the 3D shapes are:
Polyhedron – A solid shape bounded by polygons is called a polyhedron. The word polyhedra are the plural of the word polyhedron. If the line segment joining any two points on the surface of a polyhedron entirely lies inside or out the polyhedron then it is called a convex polyhedron.
Faces – Polygons forming a polyhedron are known as its faces. In other words, a face refers to any single flat surface of a 3D shape.
Edges – Line segments common to intersecting faces of a polyhedron are known as its edges.In other words, n edge is a line segment on the boundary joining one vertex (corner point) to another. It is similar to the sides we have in 2D shapes.
Vertices – Points of intersection of edges of a polyhedron are known as its vertices. In other words, the meeting point of a pair of sides of a polygon is called its vertex.
Let us now understand some of the common 3D shapes.
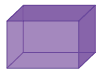
Cuboid
A 3D shape having six rectangular faces is called a cuboid, for example, a matchbox, a brick, a book etc. In other words, it is an extension of a rectangle in a 3D plane. Other examples of cuboids include almirah, room, playing board box etc. a cuboid has length, breadth and height. Various parts of a cuboid are:
Faces: A cuboid has 6 rectangular faces. The opposite faces of a cuboid are identical.
Edges: Two adjacent faces of a cuboid meet in a line segment called an edge of the cuboid. A cuboid has 12 edges.
Vertx: Three edges of a cuboid meet at a point called a vertex. A cuboid has 8 vertices
Below we have a general diagram of a cuboid
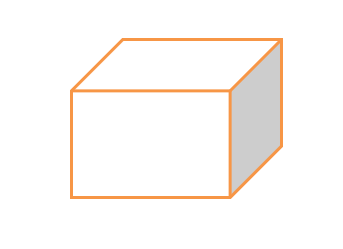
Cube
A cuboid whose length, breadth and height are equal is called a cube. Examples of a cube are sugar cubes, cheese cubes and ice cubes. In other words, it is an extension of a square in a 3D plane.
Below we have a general diagram of a cube.
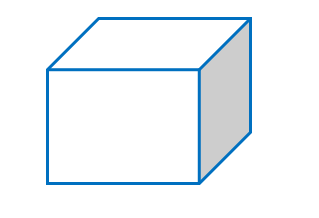
Faces: A cube has 6 rectangular faces, out of which all are identical.
Edges: A cube has 12 edges
Vertx: A cube has 8 vertices
Cylinder
A cylinder is a solid with two congruent circles joined by a curved surface. Objects such as a circular pillar, a circular pipe, a test tube, a circular storage tank, a measuring jar, a gas cylinder, a circular powder tin etc. are all shapes of a cylinder. A cylinder has a curved lateral surface and two circular faces at its ends.
Below we have a general diagram of a Cylinder.
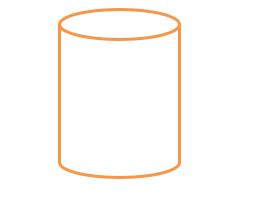
Faces: A cylinder has one curved surface and two flat faces. In other words, a cylinder has two plane faces, namely the top and the base and one curved face. The distance between the end faces of a cylinder is called its length.
Edges: A cylinder has two curved edges.
Vertx: A cylinder has no corner or vertex.
Cone
A circular cone has a circular base that is connected by a curved surface to its vertex. A cone is called a right circular cone if the line from its vertex to the centre of the base is perpendicular to the base. An ice-cream cone is an example of a cone
Below we have a general diagram of a Cone.
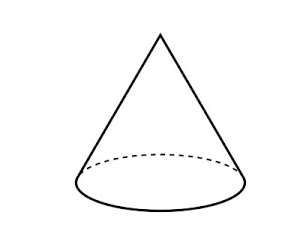
Faces: A cone has one flat face and one curved surface.
Edges: A cone has one curved edge.
Vertx: A cone has one vertex.
Sphere
A sphere is a solid formed by all those points in space that are at the same distance from a fixed point called the centre. In other words, it is an extension of a circle in a 3D plane.
Below we have a general diagram of a Sphere.
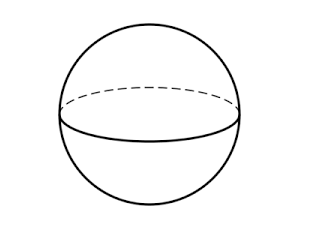
Faces: A cone has one curved surface.
Edges: A cone has no edge.
Vertx: A cone has no vertex.
Prism and Pyramids
Two important members of a polyhedron family are prisms and pyramids. Let us understand about these two polyhedrons.
Prism
A prism is a solid whose side faces are parallelograms and whose ends (bases) are congruent parallel rectilinear figures. A prism is a polyhedron that has two congruent and parallel polygons as bases. The rest of the faces are rectangles.
Base of a Prism – The end on which a prism may be supposed to stand is called the base of the prism.
Height of a Prism – The perpendicular distance between the ends of a prism is called the height of a prism.
Principal axis of a Prism – The straight line joining the centres of the ends of a prism is called the axis of the prism.
Length of a Prism – The length of a Prism is a portion of the axis that lies between the parallel ends.
Lateral faces – All faces other than the bases of a prism are called its lateral faces
Lateral edges – The lines of intersection of the lateral faces of a prism are called the lateral edges of a prism.
Regular Prism – A prism is called a regular prism if the ends are a regular prism.
Right Prism – A prism is called a right prism if its lateral edges are perpendicular to its end or bases otherwise it is called an oblique prism.
It is important to note here that in a right prism length of the prism is the same as its height. Also, all lateral edges are of the same length equal to the height of the prism. Also, we can clearly understand from the definition of a right prism that it’s all lateral faces are rectangles. The number of lateral edges and lateral faces of a prism is the same as the number of sides in the base of the prism.
A prism is also named according to its bases.
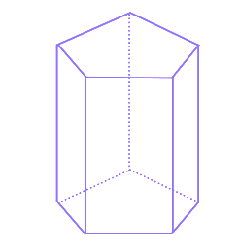
Triangular Prism
In other words, a solid whose lateral faces are rectangular and the bases are congruent triangles is called a triangular prism.
Faces: A triangular prism 3 rectangular faces and 2 triangular bases.
Edges: A triangular prism has 9 edges.
Vertx: A triangular prism has 6 vertices.
Below is the general figure of a triangular prism.

Right Triangular Prism – A right prism is called a right triangular prism if its ends are triangles. In other words, a triangular prism is called a right triangular prism if its lateral edges are perpendicular to its ends.

A Prism is said to be a quadrilateral prism or a pentagonal prism or a hexagonal prism etc. according to the number of sides in the rectilinear figure forming the ends or the bases is 4, 5 or 6. This means that:
- If the number of sides in the rectilinear figure forming the ends or the bases is 4, it is called a quadrilateral prism.
- If the number of sides in the rectilinear figure forming the ends or the bases is 5, it is called a pentagonal prism.

- If the number of sides in the rectilinear figure forming the ends or the bases is 6, it is called a hexagonal prism.

- If the end of a quadrilateral is a parallelogram then it is known as a parallelepiped.
Do you know that a cube and a cuboid are examples of prisms? A quadrilateral prism with its ends as squares is called a rectangular solid or a cuboid. A cube is a prism that has a square as a base, while a cuboid is a prism that has a rectangular base.
Pyramid
A pyramid is a polyhedron whose base is a polygon of any number of sides and other faces are triangles with the common vertex if all corners of a polygon are joined to a point not lying in its plane we get a pyramid. In other words, a pyramid is a solid whose base is a plane rectilinear figure and whose side faces are triangles having a common vertex, called the vertex of the pyramid.

Vertex – The common vertex of the triangular faces of a pyramid is called the vertex of the pyramid.
Height – The height of a pyramid is the length of the perpendicular from the vertex to the base. In other words, The length of the perpendicular drawn from the vertex of a pyramid to its base is called the height of the pyramid.
Axis – The axis of a pyramid is a straight line joining the vertex to the central point of the base.
Lateral edges – The edges through the vertex of a pyramid are known as its lateral edges.
Lateral faces – The side faces of a pyramid are known as its lateral faces.
The side faces of a pyramid form its lateral surface.
If the base of a pyramid is a polygon of n sides then it has n lateral faces each of which is a triangle and 2n edges
Therefore, we can say that a pyramid is a solid whose base is a polygon. The other faces of the pyramid are triangles that share a common vertex. This shape is actually found in Egyptian sculptures. Based on the base of the pyramid, a pyramid is of different types –
Right Pyramid
A pyramid is said to be a right pyramid if the perpendicular drawn from the vertex on the base meets the base at its central point, i.e. the centre of the inscribed or circumscribed circle. In other words, the vertex of the pyramid lies on the perpendicular to the base drawn through its centre. Otherwise, the pyramid is called an oblique prism.
Regular Pyramid
A pyramid is said to be a regular pyramid if its base is a regular figure. This means that in a regular pyramid, all sides of its base are equal.
It is important to note here that in the case of a right rectangular Pyramid the lateral edges are equal and the lateral faces are congruent triangles.
Square Pyramid
A solid whose base is a square and whose sides, faces are triangles having a common vertex is called a square pyramid. A square pyramid has 4 lateral triangular faces and 8 edges

Triangular Pyramid
A solid whose base is a triangle and whose faces are triangles having a common vertex is called a triangular pyramid.

A triangular pyramid has 3 triangular lateral faces, one triangular base and 6 edges.
A triangular pyramid is also called a tetrahedron.
Platonic Solids
A platonic solid is a polyhedron. It is interesting as well as surprising to know that there are exactly five platonic solids. These five platonic solids are tetrahedron, cube, octahedron, icosahedron, and dodecahedron.
Tetrahedron – Polyhedron or metallic solid whose faces are congruent equilateral Triangles is called the tetrahedron.
Cube – Cube is the only platonic solid whose every face is a square. Cube is also known as a hexahedron as it has 6 squares as its faces.
Tetrahedrons and cubes are platonic solids in which three faces meet at a point to form a vertex. T
Octahedron – The platonic solid which has four equilateral triangles meeting at each vertex is known as the octahedron.
Dodecahedron – A platonic solid can having every face as a pentagon is known as a dodecahedron. In a Dodecahedron, three pentagons meet at every vertex.
Euler’s Formula
Can we define a relation between the faces, vertices and edges of a polygon? Let us find out.
The number of faces (F), the number of vertices (V) and the number of edges (E), of a simple convex polyhedron are connected by the following formula:
F + V = E + 2
This is called Euler’s formula.
Key Facts & Information
- A solid shape bounded by a polygon is called a polyhedron.
- Polygons forming a polyhedron are known as at as its faces.
- Line segments come on two intersecting faces of a polyhedron are known as its edges.
- Points of intersection of edges of a polyhedron are known as its vertices.
- A polyhedron is said to be a regular polyhedron if its faces are made up of regular polygons and the same number of faces meet at each vertex.
- If the line segment joining any two points on the surface of a polyhedron entirely lies inside or out the polyhedron then it is called a convex polyhedron.
- A prism is a solid whose faces are parallelogram and whose ends or bases are congruent parallel polygons.
- A prism is called a regular prism if ends are regular polygons.
- A Prism is called a right prism if its lateral edges are perpendicular to its ends. Otherwise, it is called an oblique prism.
- A prism is called a triangular prism if its ends are triangles.
- A right prism is called a triangle right triangular prism if its ends are triangles.
- A pyramid is a polyhedron whose base is a polygon of any number of sides and other faces are triangles with a common vertex.
- A pyramid is said to be a right Pyramid in the perpendicular dropped from the vertex on the base meets the base at its Central point, i.e. the centre of the inscribed or the circumscribed circle. In other words vertex of the pyramid lies on the perpendicular to the base drawn through its centre. Otherwise, the pyramid is called an oblique prism.
- A pyramid is said to be a regular pyramid if its base is a regular figure, i.e. all sides of its base are equal.
- A pyramid is said to be a triangular pyramid if the base is a triangle. A triangular pyramid is also called a tetrahedron.
- A pyramid is called a quadrilateral pyramid if its base is a quadrilateral.
- A platonic solid is a polyhedron. There are exactly five platonic solids. These five platonic solids are tetrahedron, cube, octahedron, icosahedron, and dodecahedron.
- The number of faces (F), the number of vertices (V) and the number of edges (E), of a simple convex polyhedron are connected by the formula F +V = E + 2
Recommended Worksheets
Understanding Properties and Hierarchy of Shapes 5th Grade Math Worksheets
Classifying Shapes by Lines and Angles 4th Grade Math Worksheets
Solving Volume of Solid Figures 5th Grade Math Worksheets









