Introduction
A dodecahedron belongs to the family of platonic solids. Did you know that the Greek terms “dodeca” for “12” and “hédra” for “face or seat” were the root of its name? Hence, it is a polyhedron with 12 faces.
Dodecahedrons are frequently found in many of the buildings around us, and a deeper understanding of them will help us recognize their importance. Understanding the characteristics of a dodecahedron can be a rewarding endeavour, regardless of your interests in math, engineering, architecture, or simply the world around you.
Grade Appropriateness
The dodecahedron concept can be given to kids as early as the 3rd grade, and as they advance through middle and high school, their comprehension will continue to grow and develop.
Math Domain
The dodecahedron falls within the mathematical domain of geometry, specifically in studying 3-dimensional shapes or solids. Geometry is a vital part of math that helps us understand the properties and relations of points, lines, surfaces, and solids.
Applicable Common Core Standards
Here are a few applicable Common Core Standards for studying dodecahedrons:
CCSS.MATH.CONTENT.3.G.A.1: Understand that shapes in different categories may share attributes and that shared attributes can define a larger category.
CCSS.MATH.CONTENT.7.G.A.3: Describe the two-dimensional figures that result from slicing three-dimensional figures, as in plane sections of right rectangular prisms and right rectangular pyramids.
CCSS.MATH.CONTENT.HSG.GMD.B.4: Identify the shapes of two-dimensional cross-sections of three-dimensional objects, and identify three-dimensional objects generated by rotations of two-dimensional objects.
Definition of the Topic
A dodecahedron is a three-dimensional shape that is made up of twelve flat faces, each of which is a pentagon. The term dodecahedron comes from the Greek words ‘dodeka’ meaning ‘twelve’ and ‘hedra’ meaning ‘base’, ‘seat’, or ‘face’.

Key Concepts
Here are the main concepts we need to understand when studying dodecahedrons:
Faces: A dodecahedron has 12 faces. Each face is an identical regular pentagon.
Vertices: A dodecahedron has 20 vertices. A vertex is a point where three edges meet.
Edges: A dodecahedron has 30 edges. A line segment on the border connecting one vertex to another is known as an edge.
The volume of Dodecahedron: The formula to calculate the volume of a regular dodecahedron is: Volume=$\frac{15+7\sqrt{5}}{4}$ a3, where a is the length of the edge.
Surface Area of Dodecahedron: The formula to find the total surface area of a regular dodecahedron is: Surface Area=$3\sqrt{25+10\sqrt{5}}$ a2, where a is the length of the edge.
Discussion with Illustrative Examples
A dodecahedron is a pentagonal-shaped three-dimensional object with twelve faces. Every face is flat, in 2-D form. One of the five platonic solids is a dodecahedron.
Platonic solids are convex polyhedra with faces made of congruent regular polygons that meet at each of their vertices with the same number of faces. Three pentagonal faces meet at each of the 20 vertices of a dodecahedron, composed of 12 congruent pentagons.
Parts of Dodecahedron

The vertex is the point of intersection of three edges.
The face is the flat surface of a dodecahedron.
The edge is the line where two adjacent faces meet.
Properties of Dodecahedron
Dodecahedron is a platonic solid. Platonic solids have identical faces. In the case of a dodecahedron, the identical faces of it are all pentagons. These pentagons are regular polygons that meet to form a three-dimensional figure called a dodecahedron!
To help us identify this shape, the following are the properties of a dodecahedron:

A dodecahedron has 12 faces. Each face is a regular pentagon.
An edge is the section of a line where two faces intersect. A dodecahedron has 30 edges.
The corners of the dodecahedron, where the faces meet, are called vertices. There are 20 vertices in a dodecahedron. There are three faces at each vertex.
A dodecahedron has 160 diagonals.
The pentagonal face has a 108° angle between its two sides. The total of the angles at every vertex is 108° + 108° +108° = 324°.

Nets of Dodecahedron
A dodecahedron can be made using a geometric net. A net is a two-dimensional shape in geometry that takes on a three-dimensional appearance when folded in a particular way.
There are 43380 different nets for the regular dodecahedron. Folding the following geometric nets shown below will result in the formation of a dodecahedron.

Formulas Involving Dodecahedron

Surface Area of a Dodecahedron
The total surface area of a regular dodecahedron is the surface area of all its faces. The surface area of a dodecahedron can be calculated as:
Surface AreaDodecahedron=$3\sqrt{25+10\sqrt{5}}$ a2, where a is the length of the edge.
The surface area of a dodecahedron can also be calculated as 20.65×a2.
The total surface area of a dodecahedron is expressed in square units.
Volume of a Dodecahedron
The volume of a regular dodecahedron is the total space it occupies in a three-dimensional plane. The formula for calculating the volume of a regular dodecahedron is given by:
VolumeDodecahedron=$\frac{15+7\sqrt{5}}{4}$ a3, where a is the length of the edge.
The volume of a dodecahedron can also be approximately calculated as 7.66×a3.
The volume of a regular dodecahedron is expressed in cubic units.
Examples with Solution
Example 1
Find the surface area of a dodecahedron with an edge length of 8 cm.
Solution
Let us substitute the given edge length, a=8 cm, into the formula.
Surface Area=$3\sqrt{25+10\sqrt{5}}$ a2 (Formula)
Surface Area=$3\sqrt{25+10\sqrt{5}}$ (8)2 (Substitution)
Surface Area≈1321.33 (Simplify)
Hence, the surface area of a dodecahedron with an edge length of 8 centimetres is 1321.33 cm2.
Example 2
Calculate the volume of a regular dodecahedron whose edge length measures four units.
Solution
Using the given edge length, a=4 units, we have,
Volume=$\frac{15+7\sqrt{5}}{4}$ a3 (Formula)
Volume=$\frac{15+7\sqrt{5}}{4}$ (4)3 (Substitution)
Volume≈490.44 (Simplify)
Therefore, the volume of a regular dodecahedron whose edge length measures four units is 490.44 cubic units.
Example 3
The sum of all the edges of a dodecahedron is 180 inches. Calculate its total surface area.
Solution
We know that a dodecahedron has a total of 30 edges.
Hence, the length of each edge is $\frac{180}{30}$=6 inches.
Substituting a=6 inches into the formula to get the surface area, we have,
Surface Area=$3\sqrt{25+10\sqrt{5}}$ a2 (Formula)
Surface Area=$3\sqrt{25+10\sqrt{5}}$ (6)2 (Substitution)
Surface Area≈743.25 (Simplify)
Therefore, the surface area of the dodecahedron is 743.25 in2.
Real-life Application with Solution
A dodecahedron is limited in real-life. However, there are few dodecahedron shapes that we can find. The following dodecahedron objects can be found:
Dodecahedron Dice
Megamix Rubik’s Cube
House designs and furniture
Let us consider a real-world example. If we have a dodecahedron-shaped die (like those used in certain board games) and want to paint all the edges, how many edges would we need to paint? The answer, as we have learned, is 30. A dodecahedron has 30 edges, so we’d need to paint 30 edges.
In real life, dodecahedrons can be found in many places. One example could be a dodecahedron-shaped lamp. How many light bulbs do we need if we want to put a small light bulb at each vertex of this lamp? The solution is 20. Remember, a dodecahedron has 20 vertices. Therefore, if we wish to place a light bulb at each vertex, we need 20 light bulbs.
Practice Test
Here are some practice questions to test your understanding:
1. How many faces does a dodecahedron have?
2. If we knew that a shape has 12 faces and 20 vertices, what could it be?
3. How many bells are there if a dodecahedron-shaped toy has a small bell at each vertex?
4. How many edges does a dodecahedron have?
5. A dodecahedron-shaped lamp has an edge length measuring 5 inches. Find its surface area and volume.
Answers:
1. 20 faces
2. A dodecahedron!
3. 20 bells
4. 30 edges
5. Volume≈957.89; Surface Area≈516.14
Frequently Asked Questions (FAQs)
Are all faces of a dodecahedron the same?
Yes. All faces of a regular dodecahedron are identical to regular pentagons.
What are the real-life applications of dodecahedrons?
Dodecahedrons are used in design and architecture due to their unique and symmetrical shape. They are also used in some dice for board games.
How many vertices does a dodecahedron have?
A regular dodecahedron has 20 vertices.
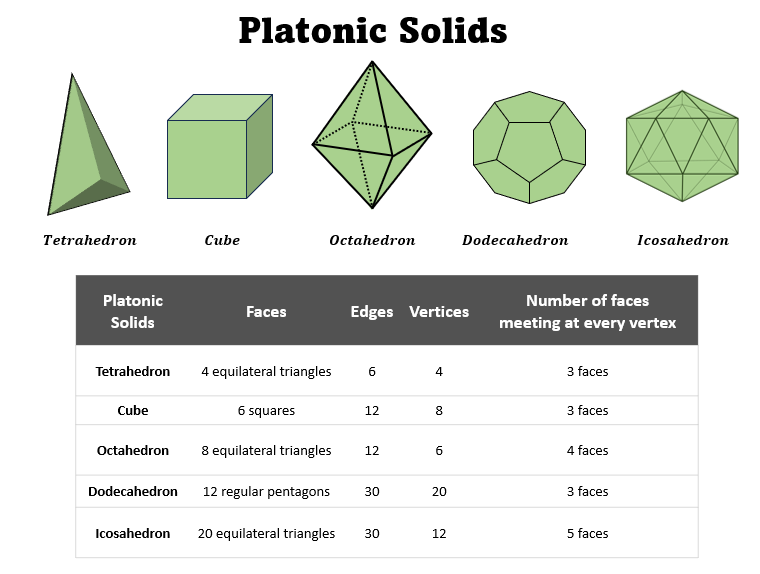
How does a dodecahedron relate to other Platonic Solids?
A dodecahedron is one of the five Platonic solids. The others are the tetrahedron, cube, octahedron, and icosahedron. The same regular polygon makes up each face of a platonic solid.
Why is it important to study dodecahedrons in math?
Studying shapes like dodecahedrons helps us understand space and the properties of different geometric shapes. It can also assist us in solving practical problems in fields like engineering, architecture, and even gaming!
Recommended Worksheets
Dodecahedron (Autumnal Equinox Day Themed) Math Worksheets
Platonic Solids (Earth Day Themed) Math Worksheets
Icosahedron (Holi Themed) Math Worksheets









