Math is used by scientists at all levels to explain their thoughts. A physicist must frequently employ extremely small or very big numbers when explaining natural parameters. Some figures are so small that they are difficult to express using standard notation. The mass of an electron, for example, is 0.000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 005
Some numbers are so big that traditional units such as millions, billions, and trillions cannot be used to describe them. The mass of the Sun, for example, is believed to be 8,000,000,000,000,000,000,000,000,000,000 kg, or 8 followed by 30 zeros. It can be difficult to write such high numbers. Engineers and physical scientists implement scientific notation to describe these values efficiently and simply. Hence we can define scientific notation as follows
Definition
A number is expressed in scientific notation as a product of any integer between 1 and 10 to the 10th power. Because it shortens the notation, scientific notation is most utilized when dealing with huge quantities or numbers with numerous digits.
General form of scientific notation
Scientific notation has a general representation of a x 10b (where “b” is an integer and “a” is any real value between 1 and 10). Only include significant figures in the real number, “a,” when writing in scientific notation.
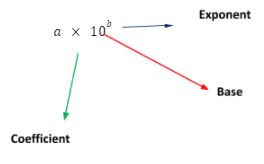
The coefficient, base, and exponent are the three main components of scientific notation.
Examples of scientific Notation
960,000,000 can be expressed as 9.6 x 108 in scientific notation. a = 9.6 b = 8 (according to general form)
0015000 can be written as 1.5 x 104 Here a = 1.5 b = 8
Some more examples of scientific notation
0.00000045 is written in scientific notation as 4.5 x 10-7
675,000,000,000 can be written as 6.75 x 1011
00583000 can be written as 5.83 x 105
0.000005000 can be written as 5x 106 OR 0.5 x 105
So, in these examples we analyzed that value of ‘’a’’ cannot be greater than 10 and b can be any integer without distinguish of positive or negative integer.
Rules for scientific notations
We must use the following rule to determine the power or exponent of ten:
- The starting point should always be ten.
- The exponent has to be a non-zero integer, which might be positive or negative.
- The coefficient’s magnitude is more than or equal to one, but it should be less than ten.
- Positive and negative numbers, as well as whole and decimal numbers, can be used as coefficients.
- The remainders of the number’s significant digits are carried by the mantissa.
- With the help of the representation below, we can see how many places we need to shift the decimal point after the single-digit value.
- If the given integer is a multiple of 10, the digits must be shifted to the left, and the power of ten will be positive.
480000000 = 4.8 × 10^8
4230000000 = 4.23 × 10^9
60500000 = 6.05 x 10^7
0.000000098 = 9.7 x 10^-8
0.0000212 = 2.12 x 10^-5 are some instances of scientific notation: 480000000 = 4.8×10^8
1230000000 = 1.23 × 10^9
50500000 = 5.05 x 10^7
0.000000097 = 9.7 x 10-8 0.0000312 = 3.12 x 10-5
How to write Scientific notation?
The large or very small number written in ordinary form is called the standard form of the number.
We can convert standard form to scientific notation and scientific notation to standard form by following simple steps.
First we see the steps for conversion of standard form to scientific notation.
Step 1:
Shift the decimal point to the left till you have a value that is higher than 1 but less than 10.
Step 2:
Look at the number of decimal places to the left of the decimal point and use that number to calculate the positive power of ten.
Step 3:
Multiply the decimal (from Step 1) by a factor of ten (in Step 2).
For a value of less than 1
Step 1:
Shift the decimal point to the right until you can get a value that is more than or equal to
Or less than 10 and equal to 1
Step 2:
Check the amount of decimal places the decimal point has been shifted to Correct, then utilize that amount as a negative power of ten
Step 3:
Multiply the decimal (from Step 1) by a factor of ten (in Step 2).
For example
0.00025 = 2.5 × 10^-4
A standard form number less than 1 has negative coefficient.
Conversion of scientific notation to standard form
Let’s see if we can return our new scientific notation numbers to their standard form.
Step 1
Start the process with the number (not the power of ten part).
Step 2
For each power of 10 you have, move the decimal point one place. Move the decimal point to the right if the powers of ten are positive. Move the decimal point one place to the left if they’re negative.
Step 3
When we’re out of digits, fill in with 0s.
Step 4
If your number is large, ensure sure the decimal places to the left of the decimal point are divided by commas into three groups of three.
For example
Scientific notation 4.45 × 10^2
1. Take the number and drop the ten and its exponent, as well as the multiplication sign (power) 4.45
2. Because the power of ten was positive, move the decimal one point to the right for each power of ten. Hence
445
3. Because there are only three digits, no commas are required.
Some example for conversion of scientific to general
1.45 × 10^-5 = 0.0000145
3.56 ×10^7 = 35,600,000
1.8945 ×10^10 = 18,945,000,000
Arithmetic in Scientific notation
Numbers expressed in scientific notation can be added, subtracted, multiplied, and divided while remaining in scientific notation.
The processes for adding and subtracting two numbers in scientific notation are listed below.
By shifting the decimal point of its decimal number, rewrite the number with the smaller exponent to have the same exponent as the number with the larger exponent.
Decimals should be added or subtracted. The power of ten is unchangeable.
If needed, convert your result to scientific notation.
Here’s an illustration.
(5.8 × 10^4) + (4.12 × 10^5)
First, observe the numbers 4 and 5 in the exponents. You’ll need to rewrite 5.8 × 10^4 to make it have a 5 exponent. Because the exponent must be increased by one, the decimal point will be moved one place to the left.
5.8 ×10^5 replace 0. 57 × 10^4
Re – write this problem now.
(0.58 × 10^5)+(4.12 ×10^5)
Then, to use what we’ve learned about decimal addition, add the decimal numbers together the power of ten remains constant.
=> 0.58+4.12
= 4.70 is the coefficient part of the scientific notation
- 4.70 × 10^5 is the required answer.
Similar for subtracting the numbers in scientific notation
For example
(1.23 × 10^6) – (1.20 × 10^6)
=1.23-1.20
:: exponent is same so it is preserved
- 0.03 × 10 ^6 is the required answer after subtraction
The processes for multiplication or division numbers in scientific notation are outlined below.
Divide or multiply the decimal numbers.
Add/subtract the exponents of the powers of ten to multiply/divide them.
If necessary, convert your solution to scientific notation.
Here’s an example of two decimal integers being multiplied.
Multiply (3.4 × 10^2) by 6.2 × 10^6.
First, use what you’ve learned about decimal multiplication to multiply the decimal numbers.
3.4×6.2=21.08
After that, add the exponents of the powers of ten.
10^2 × 10^6=10^(2+6) = 10^4
Combine the results now.
(3.4 × 10^2).(6.2 × 10^6)==(3.4 × 6.2) × (10^2 × 10^6) = 21.08 × 104
Convert your solution to scientific notation at the end. You must rewrite 21.08 × 10^8 in such a way that the decimal value is at least 1 but not more than 10. Move the decimal point to the left one space. Increase the exponent on the 10 by one to keep the overall value the same.
21.08 × 10^8 becomes 2.108 × 10^9
Here’s an illustration of how to divide two decimal integers.
Divide (8.4 × 10^5)(1.4 × 10^2)
First, use what we have learned about 8.4 ÷ 1.4= 6 to divide the decimal values.
Subtract the exponents from the powers of ten to divide them. It’s important to keep in mind that subtracting a negative number is just the same as addition the positive version.
10^5 ÷ 10^2 = 10^(5−2) = 10^3
Combine the results now.
(8.4 × 10^5) ÷ (1.4 × 10^2) = (8.4 ÷ 1.4) × (10^5 ÷ 10^2)
6 × 10^7
Last but not least, double-check that your answer is written in scientific notation. Because 6 is less than 10 but greater than 1, your answer is in scientific notation.
The solution is (8.4 × 10^ 5) ÷ (1.4 × 10^2) = 6.0 × 10^7.
How to write scientific notations in calculator
Take, for instance, the value 1.52 x 105 on a TI-30 calculator. To type this number in scientific notation, start by typing 1.52 into the calculator. After then, press the [2nd] key, followed by the x^-1 key, which has EE displayed above it. “x 10 to the power of” is what EE stands for. Type the exponent 5 after you’ve pressed the [EE] key. The display should look like this: 1.52 105 **, with a 05 in smaller print in the upper right corner of the display. The [EE] key is not available on the TI-30XS Multi-View TM scientific calculators. Instead, they offer a shortcut key, [x10n], which can be used to enter scientific notation exponents.
For a TI-83/84 calculator
Click the mode button and select SCI on the top line to keep the number you input remains in scientific notation. When you press the enter key when in NORMAL mode, the number will be extended.
Let’s utilize the same 1.52 x 10 ^5 example as the TI-30. 1.52 should be typed in. Then press the [2nd] key, followed by the [ ] “comma” key (it’s the key with the EE above it). After that, enter the exponent. It will be written as 1.52E05, which stands for 1.52 x 10 ^5
Why we use scientific notation
When we’re interested in a career in math, engineering, or science (or already work in one of these professions). We’ll almost certainly need to use scientific notation. Computer scientists and astronomy, in particular, rely on scientific notation on a daily basis since they work with microscopic particles all the way up to gigantic celestial objects and require a system that can manage such a wide range of numbers.
One of the benefits of scientific notation is that it helps you to be more precise with your numbers, which is important in those fields. Rather than rounding to a figure that is simpler to say or write, scientific notation allows you to be extremely precise with your numbers without making them unmanageable.
Writing scientific papers
In writing a scientific study article, you may need to utilize scientific notation because scientific investigations can contain very large or very small figures that must be precise. Consider the following scenario: If you’re dealing with the mass of particles or lengths in the universe, you don’t want to see pages full of numbers with digit after digit or numbers with seemingly endless zeroes! You also don’t want to round up or down too much, as this could skew your results and undermine your trustworthiness.
Use of scientific notation in science and engineering
Scientists and engineers frequently collaborate with both large and small groups of people. In this case, the standard practice of utilizing commas and leading zeroes proves to be extremely inconvenient. Scientific notation is a technique of representation that is more compact and less prone to errors. There are two parts to the number: an accuracy part (the mantissa) and a scale part (the significance) (the exponent, being a power of ten). 23,000, for example, may be written as 23 times 10 to the third power (that is, times one thousand). The exponent can be thought of as the lot of locations to the left of the decimal point. Because writing “times 10 to the X power” is inconvenient, a shorthand approach is utilized, in which the letter E replaces “times 10 to the X power” (which stands for exponent). As a result, 23,000 can be expressed as 23E3. 45E9 represents the value of 45,000,000,000.
It’s worth noting that this figure might alternatively be written as 4.5E10 or perhaps even 0.45E11. The only distinction between scientific and engineering notation is that the exponent in engineering notation is always a multiple of three. As a result, 45E9 is correct engineering notation, however 4.5E10 is not. E is commonly denoted by a “EE” or “EXP” button on most scientific calculators. Depressing the keys 4 5 EE 9 would be the procedure of entering the value 45E9.
The exponent is negative for fractional values and can be thought of as the number of places the decimal point must be pushed to the right. 0.00067 can so be written as 0.67E3, 6.7E4, or even 670E6. Only the first also last of these three can be used as engineering notation.
Engineering notation takes a step further by replacing the multiples of three for the exponent with a set of prefixes. The prefixed are as follows:
10^6 = E6 = Mega (M)
10^3 = E3 = Kilo (k)
10^9 = E9 = Giga (G)
10^12 = E12 = Tera (T)
10^-6 = E-6 = Micro () and so forth
Examples
23,000 volts, for example, can be expressed as 23E3 volts or simply 23 kilovolts.
This writing is much simpler than the standard form for processing a large range of numbers, in addition to being more concise. Simply multiply the precise parts and add the exponents when multiplication. Divide the accuracy portions and eliminate the exponents when dividing. For example, multiplying 23,000 by 0.000003 may appear to be a difficult process. This is 23E3 times 3E6 in technical notation. 69E3 is the outcome (that is, 0.069). It will become second nature after enough experience that kilo (E3) multiplied by micro (E6) equals milli (E3). This will make lab calculations a lot easier. 42,000,000 divided by 0.002 equals 42E6 divided by 2E3, or 21E9 (the exponent is 6 minus a negative 3, or 9)
Before adding different, make absolutely sure the exponents are equal (scaling if necessary) before adding or subtracting the precision sections. For instance, 2E3 plus 5E3 equals 7E3. 2E3 plus 5E6 is like 2E3 plus 5000E3, or 5002E3 by comparison (or 5.002E6).
Conclusion
Overall, scientific notation is a handy technique to write and work with extremely large or extremely small numbers. Scientific notation is useful for persons undertaking academic and professional work in math and science, even if it may seem difficult to conceive applying it in everyday life. A scientific notation calculator and converter make using this shorthand more easily for anyone studying or working in these subjects.









