Introduction
Multiplication is one of the four basic operations in mathematics with the other three being addition, subtraction and division. So, what do we mean by multiplication and how are two numbers multiplied in mathematics? Let us find out.
Suppose we have 5 pens in a box. We call this a group of 5 pens. Now, if we have another box of 5pens that would also be called a group of 5 pens. That makes two groups of 5 pens each.
Similarly, we can say that if two parrots make a group, 4 parrots would make two groups of 2 parrots each. For 3 groups of parrots to be present, we would need 3 groups having 2 parrots each.
This can be represented as –
One group of pens = 5 pens
Two groups of pens = 5 pens + 5 pens = 10 pens
Three groups of pens = 5 pens + 5 pens + 5 pens = 15 pens
Similarly,
One group of Parrots = 2 Parrots
Two groups of Parrots = 2 Parrots + 2 Parrots = 4 Parrots
Three groups of Parrots = 2 Parrots + 2 Parrots + 2 Parrots = 6 Parrots
From the above example, we can see that there are equal numbers in each group. To find the total of the groups we need to add the same number again and again.
This is what we multiplication of numbers. Multiplication of numbers is therefore nothing but repeated addition. Now, that we have understood what we mean by multiplication, let us understand the definition of multiplication in mathematical terms.
What is Multiplication?
The process of finding out the product between two or more numbers is called multiplication. The result thus obtained is called the product. Suppose you buy 6 pens on one day and 6 pens on the next day. Total pens you bought are now 2 times 6 or 6 + 6 = 12.
This can also be written as 2 x 6 = 12
Symbol for Multiplication
Note the symbol used in the example above for multiplication. The symbol (x) is generally used to represent multiplication. Other common symbols that are used for multiplication are the asterisk (*) and dot (.)
Now, let us have a look at some important terms that are used when two numbers are multiplied.
Important terms in the multiplication
Some important terms used in multiplication are –
Multiplicand – The number to be multiplied is called the multiplicand.
Multiplier – The number with which we multiply is called the multiplier.
Product – The result obtained after multiplying the multiplier and the multiplicand is called the product.
The relation between the multiplier, multiplicand and the product can be expressed as –
Multiplier × Multiplicand = Product
Let us understand this using an example.
Suppose we have two numbers 9 and 5. We wish to multiply 9 by 5.
So, we express it as 9 x 5 which gives us 45.
Therefore, 9 x 5 = 45
Here, 9 is the multiplicand, 5 is the multiplier and 45 is the product.
Now, that we have understood what we mean by multiplication and the terms associated with it, let us move to learn multiplication of 1 – digit numbers.
Multiplication by a number by 1
Let us take an example.
Suppose we have 1 leaf. Since, we know that multiplication is repeated addition, let us check what we get after adding 1 in a repeated manner. We will have,
1 leaf
1 leaf + 1 leaf =2 leaves
1 leaf + 1 leaf + 1 leaf =3 leaves
1 leaf + 1 leaf + 1 leaf + 1 leaf =4 leaves and so on
Mathematically, this can be written as
1
1 + 1 = 1 x 2 = 2
1 + 1 + 1 = 1 x 3 = 3
1 + 1 + 1 +1 = 1 x 4 = 4 and so on
From the above example, we can see that a number when multiplied with 1 will give the result as the number itself. Graphically, repeated addition of 1 can be shown as
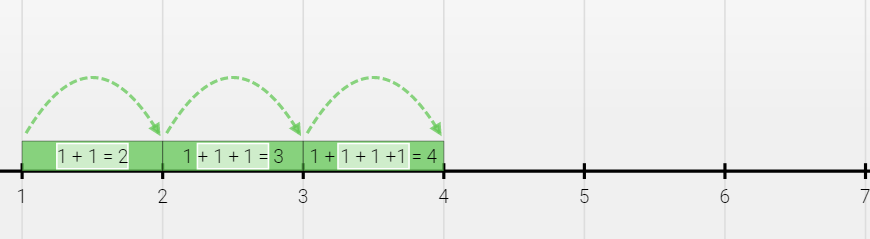
So, we have,
1 x 1 = 1
2 x 1 = 2
3 x 1 = 3
4 x 1 = 4
5 x 1 = 5
6 x 1 = 6
7 x 1 = 7
8 x 1 = 8
9 x 1 = 9
10 x 1 = 10
Multiplication by a Number by 2
Let us take an example.
Suppose we have 2 leaves. Since, we know that multiplication is repeated addition, let us check what we get after adding 2 in a repeated manner. We will have,
2 leaves
2 leaves + 2 leaves = 4 leaves
2 leaves + 2 leaves + 2 leaves = 6 leaves
2 leaves + 2 leaves + 2 leaves + 2 leaves = 8 leaves
Mathematically, this can be written as
From above we can see that multiplication by 2 is a skip counting of 2. Graphically it can be represented as –
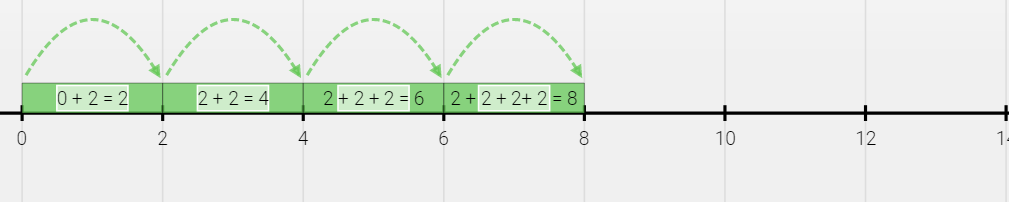
Therefore we have,
2 x 1 = 2
2 x 4 = 8
2 x 3 = 6
2 x 4 = 8
2 x 5 = 10
2 x 6 = 12
2 x 7 = 14
2 x 8 = 16
2 x 9 = 18
2 x 10 = 20
Similarly, for multiplying 3 with a single digit number we will just perform skip counting by 3 and 4 respectively.
Let us check skip counting by 5.
Multiplication by a Number by 5
Consider the grid below

In the grid above, begin at 5 and colour every fifth number. What will you get?

We can see above that the coloured boxes either end with 5 or end with 0. This is the multiplication of a number by 5.
Using skip counting, we can write it as
5
5 + 5 = 5 x 2 = 10
5 + 5 + 5 = 5 x 3 = 15
5 + 5 + 5 + 5 = 5 x 4 = 20 and so on
We can see above in the above examples, that the numbers 1, 2 and 5 can be multiplied subsequently by every number. This representation of multiplication is called as the multiplication table. Let us learn more about them.
What is a multiplication table?
A multiplication table is a list of multiples of a number. In other words, it shows the product of one number with other numbers. So, how do we get a multiplication table? We can obtain a multiplication table by multiplying the given number with whole numbers.
So, in order to multiply one digit numbers, we must be familiar with the multiplication table from 2 to 10. Let us write down the tables for one digit numbers.
Multiplication Table for One Digit Numbers
We will write each table multiplying the multiplicand from 1 to 10
Multiplication Table of 2
| 2 × 1 = 2 | 2 × 6 = 12 |
| 2 × 2 = 4 | 2 × 7 = 14 |
| 2 × 3 = 6 | 2 × 8 = 16 |
| 2 × 4 = 8 | 2 × 9 = 18 |
| 2 × 5 = 10 | 2 × 10 = 20 |
Multiplication Table of 3
| 3 × 1 = 3 | 3 × 6 = 18 |
| 3 × 2 = 6 | 3 × 7 = 21 |
| 3 × 3 = 9 | 3 × 8 = 24 |
| 3 × 4 = 12 | 3 × 9 = 27 |
| 3 × 5 = 15 | 3 × 10 = 30 |
Multiplication Table of 4
| 4 × 1 = 4 | 4 × 6 = 24 |
| 4 × 2 = 8 | 4 × 7 = 28 |
| 4 × 3 = 12 | 4 × 8 = 32 |
| 4 × 4 = 16 | 4 × 9 = 36 |
| 4 × 5 = 20 | 4 × 10 = 40 |
Multiplication Table of 5
| 5 × 1 = 5 | 5 × 6 = 30 |
| 5 × 2 = 10 | 5 × 7 = 35 |
| 5 × 3 = 15 | 5 × 8 = 40 |
| 5 × 4 = 20 | 5 × 9 = 45 |
| 5 × 5 = 25 | 5 × 10 = 50 |
Multiplication Table of 6
| 6 × 1 = 6 | 6 × 2 = 12 |
| 6 × 3 = 18 | 6 × 4 = 24 |
| 6 × 5 = 30 | 6 × 6 = 36 |
| 6 × 7 = 42 | 6 × 8 = 48 |
| 6 × 9 = 54 | 6 × 10 = 60 |
Multiplication Table of 7
| 7 × 1 = 7 | 7 × 6 = 42 |
| 7 × 2 = 14 | 7 × 7 = 49 |
| 7 × 3 = 21 | 7 × 8 = 56 |
| 7 × 4 = 28 | 7 × 9 = 63 |
| 7 × 5 = 35 | 7 × 10 = 70 |
Multiplication Table of 8
| 8 × 1 = 8 | 8 × 6 = 48 |
| 8 × 2 = 16 | 8 × 7 = 56 |
| 8 × 3 = 24 | 8 × 8 = 64 |
| 8 × 4 = 32 | 8 × 9 = 72 |
| 8 × 5 = 40 | 8 × 10 = 80 |
Multiplication Table of 9
| 9 × 1 = 9 | 9 × 6 = 54 |
| 9 × 2 = 18 | 9 × 7 = 63 |
| 9 × 3 = 27 | 9 × 8 = 72 |
| 9× 4 = 36 | 9 × 9 = 81 |
| 9 × 5 = 45 | 9× 10 = 90 |
Now, that we have understood the multiplication of one digit numbers, how do we write them? Do we use the tabular method always or we can write them using any other method? Let us find out.
Methods of multiplication
There are two methods of multiplying the numbers, namely the expanded notation method and the column method.
Expanded Notation Method
In the expanded notation method we expand the multiplicand as per the place values and then multiply each number by the multiplier. We then sum up all the results obtained to get our final answer. Let us understand it through an example.
For example, Multiply 8 by 4
Here the place value of 8 is 8 as it is a single digit number. Therefore, we will just write the multiplication of 8 with 4 as
8 x 4 = 32
Similarly, 7 multiplied by 6 will be written as 7 x 6 = 42
Column Method
In this method, we split the numbers into columns and multiply the numbers by the multiplicand one by one. There are two scenarios when using this method.
Let us understand them one by one
Multiplication without Regrouping
Suppose we want to multiply 2 by 4. We will write it as
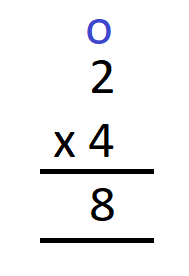
It is important to note here that the “O” above 2 in the multiplication example states above represents the place value of the number 2, which is one’s place.
In the example, above, we did not have any need for a rearrangement as we had two single digit numbers and the product obtained was also a single digit number. But, how do we go about when the product is not a single digit number? This is where the concept of regrouping pitches in. Let us find out what we mean by regrouping.
Multiplication with Regrouping
In the above case, we have small multiplications that did not involve two-digit results at any step. But in the case of larger numbers, there will be a need to carry forward the number to the number at the next place value. This is called Multiplication with Regrouping. Let us understand it through an example.
Suppose we want to multiply 8 by 9. From the multiplication table, we had obtained the value of 8 multiplied by 9 as 72. But how is it written? If we write this multiplication in the column method, we will have
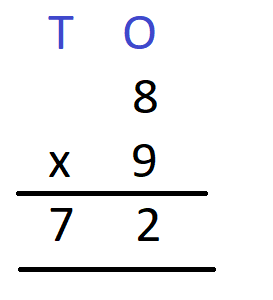
It is important to note here the alphabet “T” above represents the tens place of the place value. We can see that since the product obtained was of 2 digits, therefore, we need to move the digit 7 to the ten’s place. We have,
8 x 9 = 72.
Solved Examples
Example 1 Alice had 6 cookies. Her brother had 7 times more cookies than her. How many cookies did her brother have?
Solution We have been given that Alice had 6 cookies. Also, her brother had 7 times more cookies than her. We need to find out the number of cookies available with Alice’s brother. We have –
Cookies with Alice = 6
Cookies with her brother = 7 times 6
Note here that when say a times b, we mean that we are repeatedly adding a, the b number of times, or, in simple words, we are multiplying a by b. therefore, when we say that the cookies with Alice’s brother are 7 times the number of cookies with Alice, we mean that the number of cookies with Alice’s brother is 7 x 6.
Now, from the multiplication table, we know that
7 x 6 =42
Therefore, the number of cookies with Alice’s brother = 42
Example 2 Use multiplication tables, to find the value of
- 3 x 7 = ______________
- 6 x 4 = ______________
- 7 x 7 = ______________
- 8 x 6 = _______________
Solution We have,
- 3 x 7 = 21
- 6 x 4 = 24
- 7 x 7 = 49
- 8 x 6 = 48
Key Facts and Summary
- Repeated addition is called multiplication.
- The process of finding out the product between two or more numbers is called multiplication.
- The result thus obtained on multiplying two numbers is called the product.
- The symbol (x) is generally used to represent multiplication. Other common symbols that are used for multiplication are the asterisk (*) and dot (.)
- The number to be multiplied is called the multiplicand.
- The number with which we multiply is called the multiplier.
- The relation between the multiplier, multiplicand and the product can be expressed as Multiplier × Multiplicand = Product
- A number when multiplied with 1 will give the result as the number itself.
- A number when multiplied by 5 will always end either in “0” or in “5”.
- A multiplication table is a list of multiples of a number.
- In the expanded notation method we expand the multiplicand as per the place values and then multiply each number by the multiplier. We then sum up all the results obtained to get our final answer.
- In the column method, we split the numbers into columns and multiply the numbers by the multiplicand one by one.
Recommended Worksheets
Multiplying One-Digit Whole Numbers by Multiples of 10 3rd Grade Math Worksheets
Subtracting 2-digit Numbers and 1-digit Numbers 1st Grade Math Worksheets
Multiplication and Division Problem Solving (Halloween Themed) Math Worksheets









