Powers (Bases and Exponents)

What is an exponent?

An exponent indicates how many times the number must be multiplied by itself. Exponents are also referred to as powers or indices. Usually, the exponent is written as a superscript to the right of the base.

Consider the number 5³. 

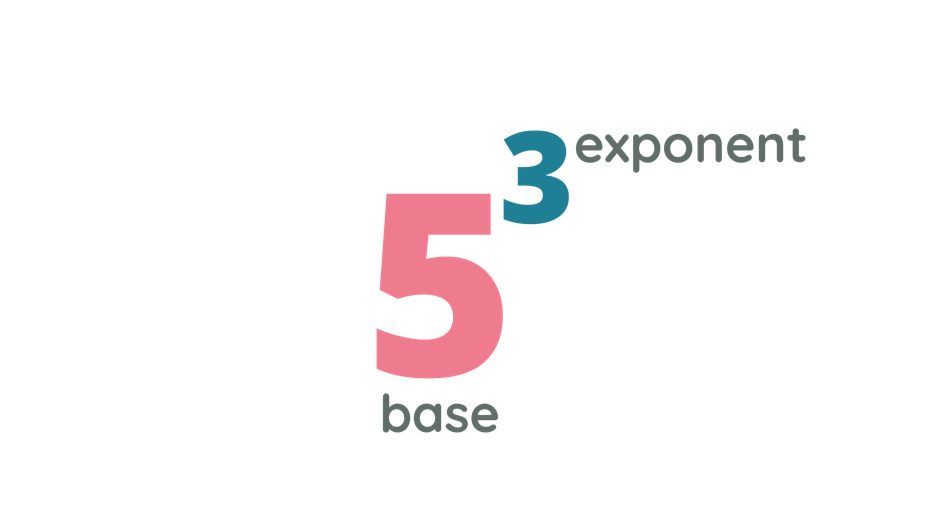
In this example, 5 is the base and 3 is the exponent. A base is a number that we will repeatedly multiply to itself, and the exponent will tell us how many times the base will be multiplied to itself. Thus, 5³ means the same thing as 5 x 5 x 5. 

For us to read 5³, we can read as:

• five raised to the power of three, 
• five raised to three, and
• five to the power of three.

Exponentiation is a mathematical operation written in the form of xⁿ, where x denotes the base and n represents the exponent. 

What is the origin of exponents?

The word power came from the Latin word potentia, potestas, dignitas which is a mistranslation of the ancient Greek term δύναμις (dúnamis), which was employed for the square of a line by Euclid, following Hippocrates of Chios. 

Meanwhile, Archimedes discovered and proved the laws of exponents in his work The Sand Reckoner. In his work, he was able to prove 10^a x 10^b = 10^{a + b}. During the 19^th century, Muhammad ibn Mūsā al-Khwārizmī introduced the terms مَال (māl, “possessions”, “property”) for a square. 

Jost Bürgi utilized exponents for Roman numerals in the late 16th century. In the 15th century, Nicolas Chuquet created a type of exponential notation that was later utilized by Henricus Grammateus and Michael Stifel in the 16th century. Michael Stifel created the term “exponent” in 1544. In 1696, Samuel Jeake introduced the term indices. 

René Descartes established the first form of our contemporary exponential notation in his treatise titled La Géométrie in the early 17th century; the notation is introduced in Book I of the text.

Leonhard Euler proposed variable exponents and, implicitly, non-integer exponents in 1748 when he wrote:

“consider exponentials or powers in which the exponent itself is a variable. It is clear that quantities of this kind are not algebraic functions, since in those the exponents must be constant.”

What are the laws of exponent?

To answer and solve problems involving exponents, the laws of exponents are fundamental. These rules are needed to be followed to be able to simplify formulas with exponents. Let’s take a look at the following rules we have for exponents! 

Product Rule

The product rule of exponents is used to multiply expressions that have the same bases. This rule states that for any non-zero term a where m and n are real numbers, 

a^m x aⁿ = a^{m + n}

This means that, to get the product of an exponent that have the same base, we are going to simply copy the base and add their exponents.

Example #1

What is the product of 5² and 5³? 

Solution

Process	Explanation
52 x 53	Set-up the multiplication process.
52 x 53 = 52 + 3	Using product rule, we will simply copy the base and add the exponents.
52 + 3 = 55	Add the exponents. Hence, 2 + 3 = 5
55 = 3125	Evaluate 55. Hence, 5 x 5 x 5 x 5 x 5 = 3125
	Therefore, the product of 52 and 53 is 55 or 3125.

Example #2

Find the product of a and a⁶.

Solution

Process	Explanation
a1 x a6	Set-up the multiplication process.
a1 x a6 = a1 + 6	Using product rule, we will simply copy the base and add the exponents. The exponent of a is 1. Hence, we will have a1 + 6
a1 + 6 = a7	Add the exponents. Hence, 1 + 6 = 7
	Therefore, the product of a and a6 is a7.

Example #3

Find the product of x³y and x³y².

Solution

Process	Explanation
(x3y)(x3y2)	Set-up the multiplication process.
(x3y)(x3y2) = x3 + 3y1 + 2	Using product rule, we will simply copy the base and add the exponents. Since we have two variables, we will still copy both bases, but take note of the exponents of each variable. Hence, we will have x3 + 3y1 + 2
x3 + 3y1 + 2 = x6y3	Add the exponents. Hence, the exponent of x will be x3 + 3 = x6  , while the exponent of will be y1 + 2 = y3
	Therefore, the product of x3y and x3y2 is x6y3.

Quotient Rule

The quotient rule of exponents is used to simplify algebraic terms or expressions that have the same bases. This rule states that for any non-zero term a where m and n are real numbers, 

$\frac{a^m}{a^n}= a^{m – n}$

This means that, to get the quotient of an exponent that has the same base, we are going to simply copy the base and subtract the exponent of the numerator by the exponent of the denominator.

Example #1

What is the quotient if 9⁷ is divided by 9³? 

Solution

Process	Explanation
$\frac{9^7}{9^3}$	Set-up the division process.
$\frac{9^7}{9^3} = 9^{7 – 3}$	Using quotient rule, simply copy the base and subtract the exponents.
97 – 3 = 94	Subtract the exponents. Hence,7 – 3 = 4
94 = 6561	Evaluate 55. Hence,9 x 9 x 9 x 9 = 6561
	Therefore, the quotient of 97 and 93 is 94 or 6561.

Example #2

Determine the quotient if a¹⁰ is divided by a⁷.

Solution

Process	Explanation
$\frac{a^10}{a^7}$	Set-up the division process.
$\frac{a^10}{a^7} =  a^{10 – 7}$	Using quotient rule, simply copy the base and subtract the exponents.
a10 – 7 = a3	Subtract the exponents. Hence,10 – 7 = 3
	Therefore, the quotient of a10 and a7 is a3.

Example #3

Find the quotient if x⁴y³ is divided by xy².

Solution

Process	Explanation
$\frac{x^{4}y^{3}}{xy^2}$	Set-up the division process.
$\frac{x^{4}y^{3}}{xy^2} =  x^{4 – 1}y^{3-2}$	Using quotient rule, copy the base and subtract the exponents. Since we have two variables, we will copy both bases, but take note of the exponents of each variable. Hence, we will have x4 – 1y3 – 2
$x^{4 – 1}y^{3-2}= x^3y$	Subtract the exponents. Hence, the exponent of x will be x4 – 1 = x3, while the exponent of will be y3 – 2 = y1.  Since the exponent of y is 1, we can simply write it as y instead of y1.
	Therefore, the quotient of x4y3 and xy2 is x3y.

Zero Exponent Rule

The zero exponent rule is used to simplify algebraic terms or expressions that have an exponent of zero. This rule simply states that if the exponent of any non-zero base a is zero, then it is always equal to 1. 

a⁰= 1

Example #1

What is the equivalent of 3⁰? 

Solution

Process	Explanation
30 = 1	By zero exponent rule, 30 is simply equal to 1.
	Therefore, 30 is equal to 1.

Example #2

Determine the value of a⁰. 

Solution

Process	Explanation
a0 = 1	By zero exponent rule, a0 is simply equal to 1.
	Therefore, a0 is equal to 1.

Example #3

Find the equivalent of x⁰y⁰. 

Solution

Process	Explanation
x0y0 = (1)(1)	By zero exponent rule,  x0 = 1, y0 = 1.
(1)(1) = 1	Get the product of 1 and 1. Thus, 1 x 1 = 1
	Therefore, x0y0 is equal to 1.

Negative Exponent Rule

The negative exponent rule is used to simplify algebraic terms or expressions that have a negative exponent. This rule states that if the exponent of any non-zero base a is negative, we need to convert it to a positive exponent by getting its reciprocal. 

$a^{-m}= \frac{1}{a^m}$

Similarly,

$\frac{1}{a^{-m}} = a^{m}$

Example #1

What is the equivalent of 2^-4? 

Solution

Process	Explanation
2-4 = $\frac{1}{2^4}$	By negative exponent rule, we will get the reciprocal of 2-4. Hence, we will have $\frac{1}{2^4}$.
$\frac{1}{2^4} = \frac{1}{16}$	Evaluate the exponent. Hence, $\frac{1}{2 × 2 × 2 × 2}$ =  $\frac{1}{16}$
	Therefore, 2-4 is equal to $\frac{1}{2^4}$ or $\frac{1}{16}$.

Example #2

Simplify a^-2. 

Solution

Process	Explanation
a-2 = $\frac{1}{a^2}$	By negative exponent rule, we will get the reciprocal of 2-4. Hence, we will have $\frac{1}{2^4}$.
	Therefore, 2-4 is equal to a-2 or $\frac{1}{a^2}$.

Example #3

What is the equivalent of $\frac{x^{-3}}{y^{-4}}$?

Solution

Process	Explanation
$\frac{x^{-3}}{y^{-4}} = (\frac{1}{y^{-4}})(\frac{1}{x^3})$	By negative exponent rule, we will get the reciprocal of x-3. Hence, we will have $\frac{1}{x^3}$. Thus, $\frac{x^{-3}}{y^{-4}} = (\frac{1}{y^{-4}})(\frac{1}{x^3})$
$(\frac{1}{y^{-4}})(\frac{1}{x^3}) = (\frac{1}{x^3})(y^4) = \frac{y^4}{x^3}$	Since we still have $\frac{1}{y^{-4}}$, we also need to get its reciprocal. Hence, $\frac{1}{y^{-4}}= y4$. Thus,
	Therefore, $\frac{x^{-3}}{y^{-4}}$ is equal to $\frac{y^4}{x^3}$.

Power of a Power Rule 

The power of a power rule is used to simplify algebraic terms where the exponent of the base is raised to another exponent, we will get the product of the two exponents. This rule states that if a non-zero term a and m and n are integers, 

(a^m)ⁿ= a^mn

Example #1

Simplify (4³)². 

Solution

Process	Explanation
(43)2 = 43 x 2	To simplify (43)2, we will use the power of the power rule. Hence, (43)2 = 43 x 2
43 x 2 = 46	Multiply the exponents. Thus, 3 x 2 = 6
46 = 4096	Evaluate 46. Thus, 4 x 4 x 4 x 4 x 4 x 4 = 4096
	Therefore, (43)2 is equal to 46 or 4096.

Example #2

Simplify (a³)⁷. 

Solution

Process	Explanation
(a3)7 = a3 x 7	To simplify (a3)7, we will use the power of the power rule. Hence, (a3)7 = a3 x 7
a3 x 7 = a21	Multiply the exponents. Thus, 3 x 7 = 21
	Therefore, (a3)7 is equal to a21.

Power of a Product Rule 

The power of a product rule is used to simplify algebraic terms with more than one variable that is being multiplied together and raised to an exponent. This rule states that if a non-zero term a and b and m is an integer, 

(ab)^m= a^mb^m

Example #1

Simplify (ab)⁸. 

Solution

Process	Explanation
(ab)8 = a8y8	To simplify (ab)8, we will use the power of a product rule. Hence, (ab)8 = a8y8
	Therefore, (x4y5)3 is equal to x12y15.

Example #2

Simplify (x⁴y⁵)³. 

Solution

Process	Explanation
(x4y5)3 = x4 x 3y5 x 3	To simplify (a3)7, we will use the power of a product rule. Hence, (x4y5)3 = x4 x 3y5 x 3
x4 x 3y5 x 3 = x12y15	Multiply the exponents. Thus,  for the exponent of x: 4 x 3 = 12 for the exponent of y: 5 x 3 = 15
	Therefore, (x4y5)3 is equal to x12y15.

Power of a Quotient Rule 

The power of a quotient rule is used to simplify the quotient of an algebraic term with more than one variable by simply distributing the exponent to the numerator and the denominator. This rule states that if a non-zero term a and b where m is an integer, 

$(\frac{a}{b})^{m}= \frac{a^m}{b^m}$

Example #1

Simplify $(\frac{4}{5})^2$ . 

Solution

Process	Explanation
$(\frac{4}{5})^2 = \frac{4^2}{5^2}$	To simplify $(\frac{4}{5})^2$, we will use the power of a quotient rule. Hence, we will distribute the exponent of 2 to the numerator and denominator. Thus, $(\frac{4}{5})^2 = \frac{4^2}{5^2}$
$\frac{4^2}{5^2} = \frac{16}{25}$	Evaluate the exponents in the denominator and denominator. Thus, numerator: 42 = 4 x 4 = 16 denominator: 52 = 5 x 5 = 25
	Therefore, $\frac{4}{5}^2$ is equal to $\frac{4^2}{5^2} or \frac{16}{25}$.

Example #2

Simplify $(\frac{a^7}{b^6})^4$ 

Solution

Process	Explanation
$(\frac{a^7}{b^6})^4 = \frac{a^{7×4}}{b^{6×4}}$	To simplify $(\frac{a^7}{b^6})^4$, we will use the power of a quotient rule. Hence, we will distribute the exponent of 4 to the numerator and denominator. Thus,  $(\frac{a^7}{b^6})^4 = \frac{a^{7×4}}{b^{6×4}}$
$\frac{a^{7×4}}{b^{6×4}} = (\frac{a^28}{b^24})$	Get the product of the exponents in the numerator and denominator, respectively. Hence,  numerator: 7 x 4 = 28 denominator: 6 x 4 = 24
	Therefore, $(\frac{a^7}{b^6})^4$ is equal to $(\frac{a^28}{b^24})$.

Example #3

Simplify $(\frac{x^3y^2}{wz^5})^6$

Solution

Process	Explanation
$(\frac{x^3y^2}{wz^5})^6 =  \frac{x^{3×6}y^{2×6}}{w^{1×6}z^{5×6}}$	To simplify $(\frac{x^3y^2}{wz^5})^6$, we will use the power of a quotient rule. Hence, we will distribute the exponent of 6 to the numerator and denominator. Thus, $(\frac{x^3y^2}{wz^5})^6 =  \frac{x^{3×6}y^{2×6}}{w^{1×6}z^{5×6}}$
$\frac{x^{3×6}y^{2×6}}{w^{1×6}z^{5×6}}= \frac{x^{18}y^{12}}{w^{6}z^{30}}$	Get the product of the exponents in the numerator and denominator, respectively. Hence, numerator (x): 3 x 6 = 18 numerator (y): 2 x 6 = 12 denominator (w): 1 x 6 = 6 denominator (z): 5 x 6 = 30
	Therefore, $(\frac{x^3y^2}{wz^5})^6$ is equal to $\frac{x^{18}y^{12}}{w^{6}z^{30}}$.

What are the common misconceptions in exponents?

When it comes to simplifying exponents, students commit errors that will result to a wrong answer. Some of these errors are listed below:

• Multiplying the base and exponent. Usually, students simply multiply the base to the number written on the exponent. 

Incorrect: 3⁴ ≠3 x 4

Correct: 3³ = 3 x 3 x 3 x 3

• Applying the power of the product rule wrong. Some students distribute the exponent even though it is not a product of two or more variables.

Incorrect: (4 + 5)² ≠ 4² + 5²

Correct: (4 + 5)² = (9)² = 81

What is the significance of exponents?

Exponents are usually used as a shortcut to represent a number that is repeatedly multiplied by itself. Most of the time, we don’t really see or use exponents in our everyday lives, but they are very significant, especially in the sciences. 

Exponents are used in showing square or cubic measurements such as square feet (ft²), square meters (m²), square inches (in²), square miles (mi²), cubic feet (ft³), cubic meters (m³). With the help of exponents, it is easier for us to distinguish square and cubic measurements. Taking measurements and calculating multi-dimensional quantities is one of the most prevalent real-world applications of exponents. Because area is a two-dimensional measure of space (length x breadth), it is always measured in square units such as square feet or square meters.

Scientists use exponents to show extraordinarily large or small numbers. With the help of exponents, writing numbers in a scientific notation became possible. In scientific notation, 150 000 can be written as 1.5 x 10⁵ – which translates to 1.5 x 10 x 10 x 10 x 10 x 10. 

Exponents are of great importance in any scientific measurement that uses a scale such as pH scale and Richter scale. The pH scale and the Richter scale are both logarithmic scales, with each whole number denoting a ten-fold rise over the previous value.

Say, for example, a scientist knows that a material with a pH of 4 indicates 10⁴, but a substance with a pH of 8 represents 10⁵. This suggests that a substance with a pH of 5 is ten times more basic than one with a pH of 4. 
Exponents are also used in computer language. We frequently hear the terms megabytes, gigabytes, and terabytes. “Mega” refers to 10⁶ or one million, “giga” refers to 10⁹, and “tera” refers to 10¹². More so, the prefixes mega- and giga- are also used in other domains such as megahertz indicates 10⁶ or one million hertz.

Recommended Worksheets

Exponents (Museum Themed) Worksheets
Understanding Exponents 6th Grade Math Worksheets
Working with Radicals and Integer Exponents 8th Grade Math Worksheets