Complex numbers

Introduction

Many of the math problems are modelled using equations. All linear equations (equations of the first degree) with real coefficients always have real solutions. However, this cannot be said about quadratic equations or equations of higher powers with real coefficients. Even starting from quadratic equations with real coefficients, equations with a negative discriminant have no real solutions. For example, equation x²+1=0 has no real solutions because the square x² cannot be equal to -1. But sometimes we do not need the solutions of the equations themselves, we need only their further application. Therefore, in order to be able to continue working on certain mathematical problems, an imaginary unit and complex numbers arose. 

Definition of complex numbers

Start with the equation x²+1=0. Take 1 to the right and get the equation x²=-1. If we denote -1 as the square of some number i, we obtain the equation x²=i² with two solutions x=i and x=-i. Note that this number i is not a real number. 

Definition: The imaginary unit i is the solution to the equation x²+1=0. Imaginary unit has the property 

i²=-1

Let’s try to see what numbers we can get by raising the imaginary unit to other powers:

i⁰=1 (Every number raised to zero power equals to 1)

i¹=i (Every number raised to the first power equals to the number itself)

i²=-1 (Property of imaginary unit)

i³=-i (i³=i²i¹=-1×i=-i)

i⁴=1 (i⁴=(i²)²=(-1)²=1)

i⁵=i (i⁵=i⁴ x i¹=1×i=i)

i⁶=-1 (i⁶=i⁴ x i²=1×(-1)=-1)

i7=-i (i7=i⁴ x i³=1×(-i)=-i)

i8=1 (i8=i⁴ x i⁴=1×1=1)

Continuing this pattern, i^4k=1, i^4k+1=i, i^4k+2=-1, i^4k+3=-i for all whole values of k. Now, consider the patterns for negative powers of imaginary unit:

i^-1=-i( i^-1=$\frac{1}{i}=\frac{i}{i^2}=\frac{i}{-1}$=-i)

i^-2=-1( i^-2=$\frac{1}{i^2}=\frac{1}{-1}$=-1)

i^-3=i (i^-3=$\frac{1}{i^3}=-\frac{1}{i}=-\frac{i}{i^2}=-\frac{i}{-1}$=i)

i^-4=1(i^-4=$\frac{1}{i^4}=\frac{1}{1}$=1)

Continuing this pattern, i^4k=1, i^4k+1=i, i^4k+2=-1, i^4k+3=-i for all negative integer values of k.

EXAMPLE: Solve the equation x²+16=0.

SOLUTION: Take 16 to the right and get the equation x²=-16. Representing -16 as the product of -1 and 16 and using the main property of imaginary unit, we get 

-16=-1×16=i² x 4²=(4i)²

Therefore, the equation becomes x²=(4i)² with two solutions x=4i and x=-4i.

This way we can solve any pure quadratic equation (quadratic equation of the type ax²+c=0) or any equation of the form axⁿ+b=0. 

Definition: Numbers of the form ai, where a is a real number and i is an imaginary unit is called pure imaginary numbers. 

Definition: A complex number is a number that can be written in the form z=a+bi, where a, b are real numbers and i is an imaginary unit. The real value a is called the real part of the complex number z which is denoted by Re(z), and b is called the imaginary part of complex number z and is denoted Im(z).

Real numbers together with pure imaginary numbers form the set of complex numbers. The set of complex numbers is denoted by C.

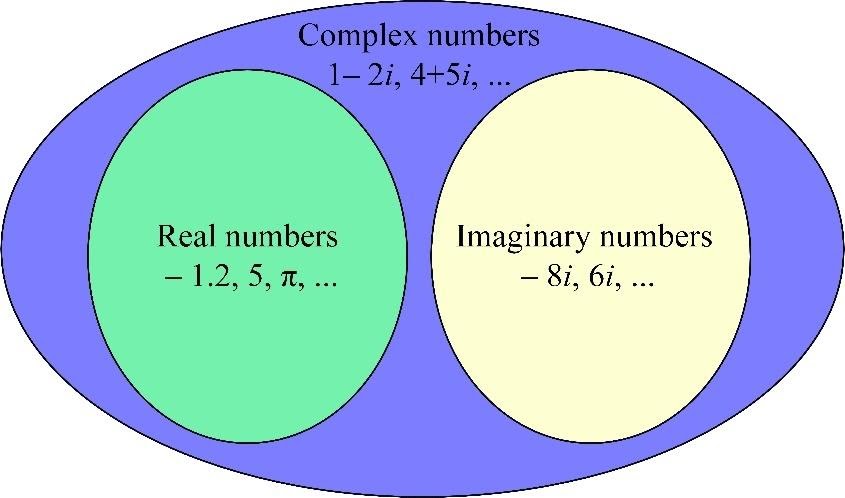
Now we can solve any quadratic equation. 

EXAMPLE: Solve the equation x²+8x+25=0.

SOLUTION: First, find the discriminant of the quadratic equation above.

D = b² – 4ac = 8² – 4×25 = 64 – 100 = -36 = 36i² = (6i)²

Using quadratic formula,

$x_1.2=\frac{-b±\sqrt{D}}{2a}=\frac{-8±\sqrt{(6i)^2}}{2⋅1}=\frac{-8±6i}{2}=-4±3i$

However, we still do not have enough data to solve an arbitrary equation of the form axⁿ+b=0.

Complex plane

Complex numbers are often represented on the complex plane. In the complex plane, there are 

• horizontal real axis, Re(z);
• vertical imaginary axis, Im(z);
• both axes are perpendicular, intersect at the origin.

To each complex number z=a+bi we can assign an ordered pair (a, b). Hence, each complex number z=a+bi can be graphed on the complex plane just as the ordered pair (a, b) would be graphed on the Cartesian coordinate plane. 

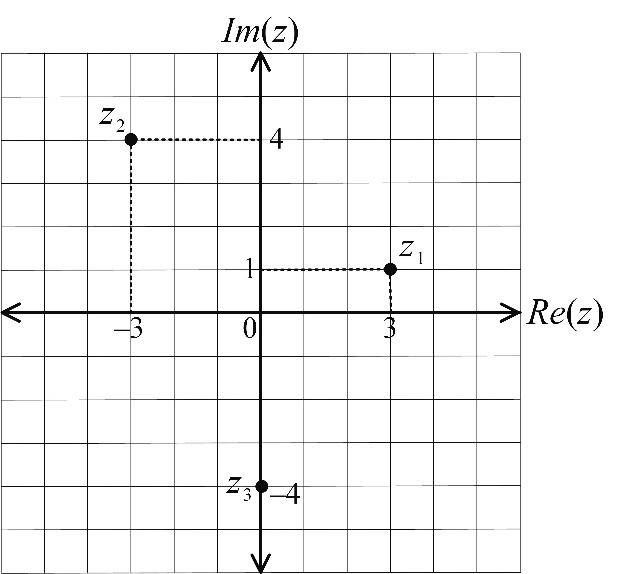
There are three complex numbers graphed on the complex plane above. 

1. Complex number z₁ is graphed as ordered pair (3, 1), so Re(z₁)=3, Im(z₁)=1 and z₁=3+i.
2. Complex number z₂ is graphed as ordered pair (-3, 4), so Re(z₂)=-3, Im(z₂)=4 and z₂=-3+4i. 
3. Complex number z₃ is graphed as ordered pair (0,-4), so Re(z₃)=0,  Im(z₃)=-4 and z₃=-4i is a pure imaginary number.

Moreover, all pure imaginary numbers lie only on the imaginary axis, all real numbers lie only on the real axis.

Different forms of complex numbers

Complex numbers have three primary forms: the general form, the polar form, and the exponential form.

If a complex number is given as z=a+bi, it is said that the complex number is given in general form. To find both polar and exponential forms of a complex number, we need to know what is the modulus and argument of complex number.

Definition: The modulus of a complex number is the distance from the complex number to 0 (to the origin) on the complex plane. The modulus of the complex number z is denoted as |z|. 

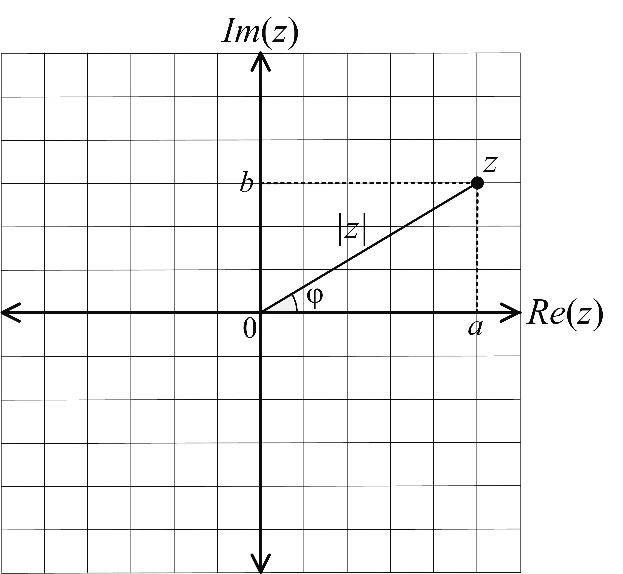
The diagram shows that on the complex plane the modulus |z| of the complex number z=a+bi is the hypotenuse of a right triangle. By the Pythagorean theorem,

|z|=$\sqrt{a^2+b^2}$

Definition: The angle that the positive real axis makes with the modulus of a complex number is called the argument of that complex number. The argument of the complex number z is denoted arg z =φ. 

Using the tangent, sine and cosine ratios,

tantan =$\frac{b}{a}, φ=\frac{b}{\sqrt{a^2+b^2}} , φ=\frac{a}{\sqrt{a^2+b^2}}$

A full rotation of a complex number z of 2π radians will produce an image that is co-terminal with the complex number. Therefore, each complex number has infinitely many arguments.

Definition: The principal value of the argument is the unique value of the argument that is in the range -π<arg⁡(z)≤π and is denoted by Arg(z).

Make the following transformations with a complex number z=a+bi:

z=a+bi=$\sqrt{a2+b2}(\frac{a}{\sqrt{a^2+b^2}}+\frac{b}{\sqrt{a^2+b^2}}i)$=|z|(cos cosφ +isin sinφ)

This way we introduce the most used polar form of the complex number 

z=|z|(cos cosφ +isin sinφ)

Now, we can introduce the third form of a complex number. First, we’ll need Euler’s formula, 

e^iφ=cos cosφ +isin sinφ

With Euler’s formula we can rewrite the polar form of a complex number into its exponential form 

z=re^iφ

where φ=Arg(z).

EXAMPLE: For given complex number, write down two other forms of this number.

a) z=1-i;

b) z=2(coscos $\frac{π}{2}$+isinsin $\frac{π}{2}$) ;

c) z=$\sqrt{3}e^{\frac{π}{3}i}$.

SOLUTION: a) Number z is given in the general form. If z=1-i, then a=1 and b=-1. Find the modulus and argument of this complex number:

|z|=$\sqrt{a^2+b^2}=\sqrt{1^2+(-1^2)}=\sqrt{2}$

coscosφ =$\frac{a}{\sqrt{a^2+b^2}}=\frac{1}{\sqrt{1^2+(-1^2)}}=\frac{1}{\sqrt{2}}$

sinsinφ =$\frac{b}{\sqrt{a^2+b^2}}=-\frac{1}{\sqrt{1^2+(-1^2)}}=-\frac{1}{\sqrt{2}}$

If cos =$\frac{1}{\sqrt{2}}$ and sin =-$\frac{1}{\sqrt{2}}$, then φ=-$\frac{\pi}{4}$ and the remaining two forms are

• polar form: z=$\sqrt{2}(coscos (-\frac{\pi}{4}) + isinsin (-\frac{\pi}{4})$ ;
• exponential form: z=$\sqrt{2}e^{-\frac{\pi}{4}i}$.

b) Number z is given in polar form. If z=2($coscos \frac{\pi}{2}) +isinsin \frac{\pi}{2}$) , then |z|=2 and φ=$\frac{\pi}{2}$. This allows us to write the exponential form of this complex number,

z=2$e^{-\frac{\pi}{2}i}$

To find the general form, simply calculate the values of corresponding trigonometric ratios:

coscos$\frac{\pi}{2}$ =0,sinsin$\frac{\pi}{2}$ =1,

then the general form of the complex number z is 

z=2(0+i⋅1)=2i

c) Number z is given in exponential form. If z=$\sqrt{3}e^{-\frac{\pi}{3}i}$, then |z|=√3 and φ=$\frac{\pi}{3}$. This allows us to write the polar form of the complex number,

z= √3(coscos $\frac{\pi}{3}$ +isinsin $\frac{\pi}{3}$)

and calculate the general form of this complex number

$z=√3(\frac{1}{2}+i⋅\frac{√3}{2})=\frac{√3}{2}+\frac{3}{2}i$

Arithmetic operations with complex numbers

ADDITION: When adding two complex numbers z₁=a₁+b₁i and z₂=a₂+b₂i, we add real part to real part and imaginary part to imaginary part.

z₁+z₂=(a₁+a₂)+(b₁+b₂)i

For example,

(3-7i)+(-2+5i)=(3+(-2))+((-7)+5)i=1-2i

SUBTRACTION: When subtracting complex number z₁=a₁+b₁i from complex number z₂=a₂+b₂i, we subtract real part of number z₁ from real part of number z₂ and imaginary part of number z₁ from imaginary part of number z₂.

z₂-z₁=a₂-a₁+b₂-b₁i

For example,

(3-7i)-(-2+5i)=(3-(-2))+((-7)-5)i=5-12i

MULTIPLICATION: When multiplying two complex numbers z₁=a₁+b₁i and z₂=a₂+b₂i, we multiply these numbers as real numbers remembering that i²=-1.

z₁z₂=(a₁a₂-b₁b₂)+(a₁b₂+a₂b₁)i

For example,

(3-7i)(-2+5i)=3⋅(-2)+3⋅5i+(-7i)(-2)+(-7i)⋅5i

=-6+15i+14i-35i²=-6+19i-35(-1)=29+19i

CONJUGATION: The conjugate z of the complex number z=a+bi is formed by taking the same real part of the complex number and changing the imaginary part of the complex number to its additive inverse.

$\overline{Z}$=a-bi

For example, 

$\overline{3-7i}$=3+7i

DIVISION: When dividing complex number z₁=a₁+b₁i by complex number z₂=a₂+b₂i, we multiply the numerator and denominator of the fraction of these numbers by the conjugate of complex number z₂.

$\frac{z_1}{z_2}=\frac{z_1}{z_2}.\frac{\overline{z_2}}{\overline{z_2}}$

For example,

$\frac{3-7i}{-2+5i}=\frac{3-7i}{-2+5i}.\frac{-2-5i}{-2-5i}=\frac{-6-15i+14i+35i^{2}}{4+10i-10i-25i^{2}}$

=$\frac{-6-i-35}{4+25}=\frac{-41-i}{29}=-\frac{41}{29}-\frac{1}{29}i$

Properties of complex numbers

CLOSURE PROPERTY: An operation is said to be closed on a set of complex numbers if the result of this operation belongs to the set of whole numbers.

If z₁ and z₂ are two complex numbers, then z₁+z₂, z₁-z₂, z₁z₂ and $\frac{z_1}{z_2}$ (z₂≠0) are complex numbers too.

COMMUTATIVE PROPERTY: An operation is said to be commutative on a set of complex numbers if when we change the order of operation, the result remains unchanged.  

If z₁ and z₂ are two complex numbers, then z₁+z₂=z₂+z₁ and z₁ x z₂=z₂ x z₁.

This property holds for addition and multiplication, but does not hold for subtraction and division.

ASSOCIATIVE PROPERTY: An operation is said to be associative on a set of whole numbers if you can rearrange the parentheses without rearranging the numbers and the result remains the same.

If z₁, z₂ and z₃ are three complex numbers, then (z₁+z₂)+z3=z₁+(z₂+z3) and (z₁ x z₂) x z3 = z₁×(z₂ x z₃).

Addition and multiplication of complex numbers are associative operations. Subtraction and division of complex numbers are not associative operations. 

DISTRIBUTIVE PROPERTY: when we multiply the sum (difference) of two numbers by a third number, then it will give the same result as multiplying each number individually by the number and then adding (subtracting) each of the multiplication results.

If z₁, z₂ and z₃ are three complex numbers, then 

(z₁+z₂) x z₃ = (z₁ x z₃)+(z₂ x z₃)  and  (z₁-z2) x z₃=z₁ x z₃ – z₂ x z₃.

ADDITIVE IDENTITY: The set is said to have an additive identity if the sum of any number from the set and this additive identity is the number itself. Usually, we denote additive identity as 0.

If z is a complex number, then z+0=0+z=z.

The additive identity for complex numbers is a complex number 0 that can be represented as 0+0i or as ordered pair (0, 0) on the complex plane. 

MULTIPLICATIVE IDENTITY: The set is said to have a multiplicative identity if the product of any number from the set and this multiplicative identity is the number itself. Usually, we denote multiplicative identity as 1.

If z is a complex number, then z×1=1×z=z.

The multiplicative identity for complex numbers is a complex number 1 that can be represented as 1+0i or as ordered pair (1, 0) on the complex plane.

MULTIPLICATION BY ZERO: When a complex number is multiplied to 0, the result is always 0.

If z is a complex number, then z×0=0×z=0

INVERSE PROPERTY: A set has the inverse property under an arithmetic operation if every element of the set has an inverse element. An inverse of an element is another element in the set that, when combined on the right or the left through the operation, always gives the identity element as the result. An inverse under addition to complex number z usually is denoted as -z. 

If z is a complex number, then z+(-z)=(-z)+z=0

An inverse under addition to complex number z=a+bi is complex number -z=-a-bi.

An inverse under multiplication to complex number z usually is denoted as z^-1. 

If z is a non-zero complex number, then z×z^-1=z^-1×z=1

An inverse under multiplication to complex number z=a+bi is the reciprocal of this complex number 

z^-1=$\frac{1}{a+bi}=\frac{1}{a+bi}.\frac{a-bi}{a-bi}=\frac{a-bi}{a^2+b^2}=\frac{a}{a^2+b^2}-\frac{b}{a^2+b^2}i$

CONJUGATE PROPERTIES: If z₁ and z₂ are two complex numbers, then

• $\overline{z_1+z_2}=\overline{z_1}+\overline{z_2}$;
• $\overline{z_1-z_2}=\overline{z_1}-\overline{z_2}$;
• $\overline{z_1 x z_2}=z_1 x z_2$;
• $\frac{\overline{z_1}}{z_2}=\frac{\overline{z_1}}{z_2}$;
• ($\overline{z}$)=z;
• $\overline{z}$=z if and only if z is a real number.

Identities with complex numbers

This section gives a summary of some of the most useful mathematical identities for complex numbers.

IDENTITIES WITH CONJUGATES:

IDENTITY 1: If z is a complex number, then $z×\overline{z}$=|z|².

Let z=a+bi, then $\overline{z}$=a-bi and 

$z×\overline{z}$=(a+bi)(a-bi)=a²-abi+abi-b²i²=a²-b² (-1)=a²+b²=|z|²

IDENTITY 2: If z is a complex number, then $\frac{z+\overline{z}}{2}$=Re(z).

Let z=a+bi, then $\overline{z}$=a-bi and 

$\frac{z+\overline{z}}{2}=\frac{a+bi+a-bi}{2}=\frac{2a}{2}$=a=Rez

IDENTITY 3: If z is a complex number, then $\frac{z-\overline{z}}{2i}$=Im(z).

Let z=a+bi, then $\overline{z}$=a-bi and 

$\frac{z-\overline{z}}{2i}=\frac{a+bi-(a-bi)}{2i}=\frac{a+bi-a+bi}{2i}=\frac{2bi}{2i}$=b=Imz

IDENTITIES WITH MODULUSES AND ARGUMENTS:

IDENTITY 4: If z is a complex number with argument φ, then coscosφ =$\frac{e^{iφ}+e^{-iφ}}{2}$ , sinSinφ =$\frac{e^{iφ}-e^{-iφ}}{2i}$

By Euler’s formula,

eiφ=coscosφ +isinsinφ

e^-iφ=coscos (-φ) +isinsin (-φ)=coscos φ – isinsin φ  

Add and subtract these two equalities:

e^iφ+e^-iφ=2coscos φ

e^iφ-e^-iφ=2isinsin φ

Then 

coscosφ =$\frac{e^{iφ}+e^{-iφ}}{2}$, sinsin φ =$\frac{e^{iφ}-e^{-iφ}}{2i}$

In order not to overload and tire the reader with long formulas, we will leave more complex identities and inequalities without proofs.

IDENTITY 5: If z₁, z₂ are two complex numbers, then |z₁ x z₂|=|z₁|×|z₂|, $|\frac{z_1}{z_2}|=\frac{|z_1|}{|z_2|}$.

IDENTITY 6: If z₁, z₂ are two complex numbers, then Arg (z₁ x z₂)=Arg(z₁)+Arg(z₂), Arg ($\frac{z_1}{z_2}$)=Arg(z₁)-Arg(z₂).

NON-TRIVIAL IDENTITY WITH FOUR COMPLEX NUMBERS:

IDENTITY 7: If z₁, z₂, z₃, z₄ are four complex numbers, then 

(z₁-z₂)(z₃-z₄) + (z₁-z₄)(z₂-z₃) = (z₁-z₃)(z₂-z₄)

TRIANGLE INEQUALITY:

If z₁, z₂ are two complex numbers, then

|z₁+z₂| ≤ |z₁| + |z₂|  and  ||z₁| – |z₂|| ≥ |z₁-z₂|

DE MOIVRE’S THEOREM:

(coscos φ + isinsin φ )ⁿ=coscos nφ +isinsin nφ ,  n is an arbitrary integer

EXAMPLE: Calculate (-1+i)²⁰²².

SOLUTION: First, represent complex number z=-1+i in the polar form. If z=-1+i, then a=-1, b=1 and

|z|=$\sqrt{(-1)^2+1^2}$=√2

coscos φ =$\frac{a}{\sqrt{a^2+b^2}}=\frac{-1}{\sqrt{2}}$

sinsin φ =$\frac{b}{a^2+b^2}=\frac{-1}{\sqrt{2}}$

This gives us φ=$\frac{3π}{4}$ and z=√2(coscos $\frac{3π}{4}$ +isinsin $\frac{3π}{4}$) .

By de Moivre’s theorem,

(coscos $\frac{3π}{4}$ +isinsin $\frac{3π}{4}$)²⁰²²=coscos ($\frac{3π}{4}$⋅2022) +isinsin ($\frac{3π}{4}$⋅2022)

and

(-1+i)²⁰²²=(√2(coscos $\frac{3π}{4}$ +isinsin $\frac{3π}{4}$))²⁰²²

=( √ 2)²⁰²² (coscos ($\frac{3π}{4}$⋅2022) +isin ($\frac{3π}{4}$⋅2022)) =2¹⁰¹¹(coscos $\frac{3033π}{2}$ +isinsin $\frac{3033π}{2}$)

Since $\frac{3033π}{2}$=1516π+$\frac{π}{2}$, then 

coscos $\frac{3033π}{2}$ =coscos (1516π+$\frac{π}{2}$)=coscos $\frac{π}{2}$  =0

sinsin $\frac{3033π}{2}$ =sinsin (1516π+$\frac{π}{2}$)=sinsin $\frac{π}{2}$  =1

and (-1+i)²⁰²²=2¹⁰¹¹ (0+i⋅1)=2¹⁰¹¹i

ROOT OF A COMPLEX NUMBER:

$\sqrt[n]{z}$={$\sqrt[n]{|z|}$(coscos $\frac{φ+2πk}{n}$ +isinsin $\frac{φ+2πk}{n}$)}, k=0, 1, 2, …, n

EXAMPLE: Solve the equation x⁴+81=0. 

SOLUTION: Rewrite the equation x⁴+81=0 as follows

x⁴=-81

This equation has no real solutions. Let us consider number -81 as a complex number. In this case, x=$\sqrt[4]{-81}$ and we can apply root of a complex number algorithm to find all complex solutions to the equation.

First, represent complex number z=-81 in the polar form:

|z|=$\sqrt{(-81)^2+0^2}$=81

coscos φ =$\frac{-81}{81}$=-1,sinsin φ =$\frac{0}{81}$=0

Therefore, φ=π and z=81(coscos π+isinsin π). 

Now, find all four roots taking into account that k=0, 1, 2, 3:

• when k=0,
  x₁=$\sqrt[4]{81}$(coscos $\frac{π+2π⋅0}{4}$ +isinsin $\frac{π+2π⋅0}{4}$) =3(coscos $\frac{π}{4}$ +isinsin $\frac{π}{4}$ =3($\frac{\sqrt{2}}{2}+i\frac{\sqrt{2}}{2}$);
• when k=1,
  x₂=$\sqrt[4]{81}$(coscos $\frac{π+2π⋅1}{4}$ +isinsin $\frac{π+2π⋅1}{4}$) =3(coscos $\frac{3π}{4}$ +isinsin $\frac{3π}{4}$ =3(-$\frac{\sqrt{2}}{2}+i\frac{\sqrt{2}}{2}$);
• when k=2,
  x₃=$\sqrt[4]{81}$(coscos $\frac{π+2π⋅2}{4}$ +isinsin $\frac{π+2π⋅1}{4}$) =3(coscos $\frac{5π}{4}$ +isinsin $\frac{5π}{4}$ =3(-$\frac{\sqrt{2}}{2}-i\frac{\sqrt{2}}{2}$);
• when k=3,
  x₁=$\sqrt[4]{81}$(coscos $\frac{π+2π⋅3}{4}$ +isinsin $\frac{π+2π⋅1}{4}$) =3(coscos $\frac{7π}{4}$ +isinsin $\frac{7π}{4}$ =3($\frac{\sqrt{2}}{2}-i\frac{\sqrt{2}}{2}$);

So, the solutions to the equation x⁴+81=0 are 3($\frac{\sqrt{2}}{2}+i\frac{\sqrt{2}}{2}$); 3(-$\frac{\sqrt{2}}{2}+i\frac{\sqrt{2}}{2}$); 3(-$\frac{\sqrt{2}}{2}-i\frac{\sqrt{2}}{2}$); and 3($\frac{\sqrt{2}}{2}-i\frac{\sqrt{2}}{2}$).

Summarizing all the above, we can conclude that complex numbers make it possible to obtain all solutions to the polynomial equations. In general, the fundamental theorem of algebra states that every non-constant single-variable polynomial with complex coefficients has at least one complex root. This theorem can be rephrased as follows: every non-zero polynomial with complex coefficients and degree of n has exactly n complex roots.

Quiz

1. Calculate the following powers of imaginary unit.

a) i²³;

b) i²⁰²²;

c) i^-19.

SOLUTION: We know that i¹=i, i²=-1, i³=-i and i⁴=1.

a) Since 23=4⋅5+3, we have 

i²³=i^4⋅5+3=(i⁴)⁵ x i³=1⁵ x (-i)=-i

b) Divide 2022 by 4 with remainder:

2022=505⋅4+2

Then

i²⁰²²=i^505⋅4+2=(i⁴)⁵⁰⁵ x i²=1⁵⁰⁵ x (-1)=-1

c) Divide 19 by 4 with remainder:

19=4⋅4+3

Then

i^-19=i^-4⋅4-3=(i⁴)^-4 x i^-3=1^-4 x $\frac{1}{i^3}$ = $\frac{1}{i^3}$ = $\frac{i}{i^4}$ = $\frac{i}{1}$=i

ANSWER: a) -i; b) -1; c) i.

2. If z₁=2-i and z₂=3+4i, calculate:

a) z₁+z₂;

b) z₁-z₂

c) z₁ x z₂;

d) $\frac{z_2}{z_1}$.

SOLUTION: a) z₁+z₂=(2-i)+(3+4i)=(2+3)+(-1+4)i=5+3i.

b) z₁ – z₂=(2-i)-(3+4i)=2-i-3-4i=(2-3)+(-1-4)i=-1-5i.

c) z₁ x z₂=(2-i)(3+4i)=6+8i-3i-4i²=6+5i-4(-1)=10+5i.

d) z₁ ÷ z₂=$\frac{3+4i}{2-i}$=$\frac{3+4i}{2-i}.\frac{2+i}{2+i}$=$\frac{6+3i+8i+4i^2}{4+2i-2i-i^2}$=$\frac{6+11i-4}{4-(-1)}$=$\frac{2+11i}{5}$=$\frac{2}{5}+\frac{11}{5}i$ 

ANSWER: a) 5+3i; b) -1-5i; c) 10+5i; d) $\frac{2}{5}+\frac{11}{5}i$

3. For given complex number, write down two other forms of this number.

a) z=-4i;

b) z=2(coscos $\frac{\pi}{6}$ +isinsin$\frac{\pi}{6}$) ;

c) z=$\sqrt{2e}^{-\frac{\pi}{4}i}$.

SOLUTION: a) Number z is given in the general form. If z=-4i, then a=0 and b=-4. Find the modulus and argument of this complex number:

|z|=$\sqrt{a^2+b^2}=\sqrt{0^2+(-4)^2}=\sqrt{16}$=4

coscos φ=$\frac{a}{\sqrt{a^2+b^2}}=\frac{0}{\sqrt{0^2+(-4)^2}}$=0

sinsin φ=$\frac{b}{\sqrt{a^2+b^2}}=\frac{-4}{\sqrt{0^2+(-4)^2}}$=-1

If coscosφ =0 and sinsinφ =-1, then φ=-$\frac{\pi}{2}$ and the remaining two forms are

• polar form: z=4(coscos (-$\frac{\pi}{2}$) +isinsin (-$\frac{\pi}{2}$)) ;
• exponential form: z=$4e^{-\frac{\pi}{2}i}$.

b) Number z is given in polar form. If z=2(coscos $\frac{\pi}{6}$ +isinsin $\frac{\pi}{6}$) , then |z|=2 and φ=$\frac{\pi}{6}$. This allows us to write the exponential form of this complex number,

z=$2e^{\frac{\pi}{6}i}$

To find the general form, simply calculate the values of corresponding trigonometric ratios:

coscos $\frac{\pi}{6}$ =$\frac{\sqrt{3}}{2}$,sinsin $\frac{\pi}{6}$ =$\frac{1}{2}$,

then the general form of the complex number z is 

z=2($\frac{√3}{2}+i⋅\frac{1}{2}$)=√3+i

c) Number z is given in exponential form. If z= √2$e^{-\frac{\pi}{4}i}$, then |z|=√2 and φ=-$\frac{\pi}{4}$. This allows us to write the polar form of the complex number,

z=2(coscos (-$\frac{\pi}{4}$) +isinsin (-$\frac{\pi}{4}$))

and calculate the general form of this complex number

z=√2($\frac{√2}{2}-i⋅\frac{√2}{2}$)=1-i

ANSWER: a) polar form: 4(coscos (-2) +isinsin (-2)) , exponential form: 4$e^{-\frac{\pi}{2}i}$

b) exponential form: 2$e^{-\frac{\pi}{6}i}$; general form: √3+i; 

c) polar form: √2(coscos (-$\frac{\pi}{4}$) +isinsin (-$\frac{\pi}{4}$)) ; general form: 1-i.

4. Calculate (1-√3i)¹⁵.

SOLUTION: First, represent complex number z=1-√3i in the polar form. 

If z=1-√3i, then a=1, b=-√3 and

|z|=$\sqrt{1^2+(-√3)^2}$=√4=2

coscos φ =$\frac{a}{\sqrt{a^2+b^2}}=\frac{1}{2}$

sinsin φ =$\frac{b}{\sqrt{a^2+b^2}}=\frac{-√3}{2}$

This gives us φ=-$\frac{\pi}{3}$ and z=2(coscos (-$\frac{\pi}{3}$) +isinsin (-$\frac{\pi}{3}$)) .

By de Moivre’s theorem,

(coscos (-$\frac{\pi}{3}$) +isinsin (-$\frac{\pi}{3}$))¹⁵=coscos (-$\frac{\pi}{3}$.15) +isinsin (-$\frac{\pi}{3}$.15) =coscos (-5π) +isinsin (-5π)

and

(1-√3i)¹⁵=(2(coscos (-$\frac{\pi}{3}$) +isinsin (-$\frac{\pi}{3}$)))¹⁵=2¹⁵ (coscos (-5π) +isinsin (-5π)

Since -5π=-6π+π, then 

coscos (-5π) =coscos (-6π+π)=coscos π =-1

sinsin (-5π) =sinsin (-6π+π)=sinsin π =0

and (1-√3i)¹⁵=2¹⁵(-1+i⋅0)=-2¹⁵

ANSWER: -2¹⁵

5. Solve the equation. 

a) x⁴-16=0;

b) x³+27=0. 

SOLUTION: a) First, factorize the left part of the equation x⁴-16=0:

(x²-4)(x²+4)=0

(x-2)(x+2)(x²+4)=0

If the product of three factors is zero, then either the first or second or third factor is 0. So,

x-2=0  or  x+2=0  or  x²+4=0

From the first equation x=2, from the second equation x=-2.The third equation has no real solutions. Find complex solutions of the equation x²+4=0. Rewrite it as follows:

x²=-4

Remembering that i²=-1, we have 

x²=4i²

and x=2i  or  x=-2i

b) If x³+27=0, then x³=-27 and x=$\sqrt[3]{-27}$. 

Represent number -27 as a complex number. First, represent complex number z=-27 in the polar form:

|z|=$\sqrt{(-27)^2+0^2}$=27

coscos φ =$\frac{-27}{27}$=-1,sinsinφ =$\frac{0}{27}$=0

Therefore, φ=π and z=27(coscosπ +isinsinπ ). 

Now, find all four roots taking into account that k=0, 1, 2:

• when k=0, x₁=$\sqrt[3]{27}coscos \frac{π+2π⋅0}{3} +isinsin \frac{π+2π⋅0}{3} =3(coscos \frac{\pi}{3} +isinsin \frac{\pi}{3}) =3(\frac{1}{2}+i\frac{√3}{2}$);

• when k=1, x₂=$\sqrt[3]{27}coscos \frac{π+2π⋅1}{3} +isinsin \frac{π+2π⋅1}{3}$=3(coscos π + isinsin π)=3(-1+i⋅0)=-3;

• when k=2, x₃=$\sqrt[3]{27}coscos \frac{π+2π⋅2}{3} +isinsin \frac{π+2π⋅2}{3} =3(coscos \frac{5π}{3} +isinsin \frac{5π}{3}) =3(\frac{1}{2}-i\frac{√3}{2})$.

So, the solutions to the equation x³+27=0 are 3($\frac{1}{2}+i\frac{√3}{2}$), -3 and 3($\frac{1}{2}-i\frac{√3}{2}$).

ANSWER: a) 2, -2, 2i and -2i;

b) 3($\frac{1}{2}+i\frac{√3}{2}$), -3 and 3($\frac{1}{2}-i\frac{√3}{2}$).

Conclusions

1. Real numbers and pure imaginary numbers are subsets of the set of complex numbers.
2. Each complex number can be represented on the complex plane as an ordered pair. 
3. Complex numbers have three main forms: general, polar and exponential.
4. We can complete with complex numbers the same arithmetic operations as with real numbers remembering the main imaginary property i²=-1.
5. Complex numbers have the same properties as real numbers. 
6. There is a range of identities with complex numbers.
7. Complex numbers greatly simplify our lives in solving equations. We know that every polynomial equation has as many roots as the degree of that equation. These roots can be real or complex, counted the multiplicity of these roots.
8. There are a number of problems that require complex numbers when solving, but ultimately give a real solution. You will encounter such problems, for example, when studying differential equations.

Recommended Worksheets

Complex Fractions (Fashion Themed) Worksheets
Applying the Properties of Equalities Involving Linear Equations 7th Grade Math Worksheets
Solving Linear Equations in One Variable Integral Coefficients and Rational Coefficients 8th Grade Math Worksheets