Comparison of Numbers is the process of defining similarities between two numbers and identifying the number greater than, smaller than, or equal to the other number. In Mathematics, there are several basic comparison rules. These are greater than (>), less than (<), and equal (=).
For young learners to be able to compare numbers, they must have a thorough understanding of the numbers and their meanings. Hands-on learning can be crucial for achieving this understanding, which includes the use of manipulatives and other devices.
Take two numbers a and b
- a > b means a is greater than b;
- a < b means a is less than b;
- a = b means a is equal to (or has the same value as)b.
To illustrate, if you asked a student which is more, 3 or 4, the student must understand that the word “three” stands for the symbol 3. This also applies to number 4. But once a student has grasped this fundamental knowledge, they can begin to study number comparison.
Why is comparing numbers important?
The ability to compare numbers plays an important role in building students’ number sense. Students with number sense are able to recognize a number, its value, and its relation to other numbers. The evaluation of numbers allows for the development of this last component.
In order to compare numbers, it is necessary for students to understand what the numbers are and the value they have. The understanding can be basic, and it can involve manipulatives and other hands-on aids.
How to Compare Numbers?
These are the following ways of comparing numbers:
- Using counting
- Using number line
- Using ordering
Using Counting
There is no question that a number with more digits is usually higher than one with fewer digits.
When any numbers have the same number of digits, once we come across unequal digits, we compare them based on the leftmost digit.
Using Number Line
When comparing two numbers, you can use a number line to determine which number is greater. Usually, the number on the right is greater than the number on the left. As you can see from the illustration below, 4 is greater than 2 since it is to the right of 2.
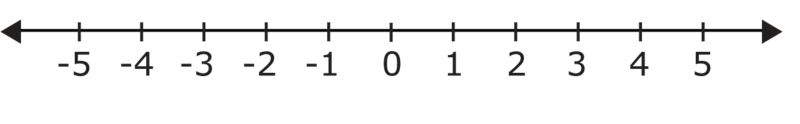
Using ordering
The arrangement of objects, numbers, etc in ascending or descending order of their values after comparison is called ordering.

Reference: https://hindisutra.com/wp-content/uploads/2020/06/Ascending-Order-Descending-Order-in-hindi.jpg
Representation
The process of comparison is the way we determine whether different objects have similar properties to each other. In Mathematics, this is the primary concept for describing whether two numbers are equal, or if one is greater or smaller than the other.
When comparing numbers, there are three special symbols used. The basic symbols used in the comparison of numbers are given below:
- Greater than (>)
- Less than (<)
- Equals to (=)
Less than (<) is true if the left value is lower than the right value, otherwise, it is false.
When the left value is larger than the right value, greater than (>) returns true, otherwise, the return will be false.
Less than or equal to (<=) returns true if the value on the left is less than or equal to the value on the right, otherwise, it returns false.
In the case that the left-hand value exceeds or equals the right-hand value, greater than or equal to (>=) returns true, otherwise it returns false.
If the left value is equal to the right value, then equal to (=) returns true, otherwise it returns false.

Greater than

Lesser than

Equal to
The above symbols can be used to compare two numbers of any type, such as natural numbers, whole numbers, integers, decimal numbers, etc. Thus the comparison of numbers is the process by which one compares and explores the differences between two numbers.
| – minus/negative | + plus/positive | X Multiplied by | ÷ Divided by | = Equals |
| ≠ Is not equal to | ≈ Is approximately equal to | ~ Is Equivalent to | ≡ Is identical to | ≢ Is not identical to |
| ± Plus or minus | ≤ Is less than or equal to | > Is greater than | ≥ Is greater than or equal to | < Is equal to |
Rules for Comparison of Numbers
There are certain mathematical rules that help us to compare numbers. Listed below are a few of them:
- Numbers with a different number of digits
- Numbers with the same number of digits
- Numbers with a different number of digits
- Numbers with more digits are always greater among the given, and numbers with fewer digits are always smaller.
Example: Of the four numbers given 9999, 55, 2, 333, 9999 is the greatest number since it has four digits. The smallest number is 2, which has only one digit.
Based on the given rule, the following conclusions can be drawn:
- A two-digit number is always greater than a one-digit number
- A three-digit number is always greater than a two-digit number
- A four-digit number is always greater than a three-digit number
- A five-digit number is always greater than a four-digit number, and so on.
| Digit | Greater | Smaller |
| Two | 99 | 10 |
| Three | 999 | 100 |
| Four | 9999 | 1000 |
| Five | 99999 | 10000 |
| Six | 999999 | 100000 |
Numbers With the Same Number of Digits
When comparing numbers with the same digits, we start from the extreme leftmost digit. Thus, the number with the greatest extreme leftmost digit is the greater number.
Example 1: Compare the numbers 632 and 529.
Based on a comparison of the left-most digits of two numbers, 6 is greater than 5 in this case.
Therefore, 632 is greater than 529. When the left-most digits of the numbers are equal, we compare the next digit rightward, and so on.
Example 2: Compare the numbers 572 and 518.
In the given example above, the number of digits is the same, and the leftmost digit (5) is the same. The next step is to compare the numbers towards the right, such as (7) and (1).
Therefore, 572 is the greater number.
Greater Than Type Operator
Taking two numbers and comparing them according to their absolute values allows us to determine which number is greater.
Example: In the numbers 3 and 2, we know that 3 is greater than 2.
We can use one special symbol (>) for “Greater than”, and it is called a greater than sign. So, the above relation can be represented as 3 > 2.
Let us consider the example:
3 > 2
A greater than sign signifies that 3 is greater than 2, which is represented mathematically by the greater than sign. Therefore, there are two points on the left side and only one point on the right side of the greater than sign.
The wide-open side of the sign is always facing towards the larger number, and the narrow endpoint is facing towards the smaller number.

Here are some examples:
- 22>11
- 555>122
- 25>23
- 1001>1000
Less Than Type Operator
By comparing two numbers, based on their absolute value, we can determine which number is smaller.
Example: In the numbers 3 and 2, we know that 2 is smaller than 3.
We use the symbol (<) for “Less than”, and it is called a less-than sign. So, the above relation can be represented as 2 < 3.
Let us consider the example:
2 < 3
In this case, 2 is smaller than 3, which is symbolized by the less-than sign in mathematics. On the right side, there are two points, and on the left, there is only one point.
The wide-open side of the sign always faces towards the greater number, and the narrow endpoint faces towards the smaller number.
Examples:
- 22<25
- 111<1111
- 5500<50000
- 9999<10001
Tricks For Comparison of Numbers
As we know, for comparing the greater and smaller numbers, we have some mathematical symbols. Even though the greater than and less than signs have clear meanings, they can be difficult to remember. With the exception of the “does not equal” sign, they all resemble one another. Then how are you going to remember them? Here are a few simple tricks.
- Alligator Method
To memorize the greater than and less than signs, imagine them as little alligators (or crocodiles), with the numbers on either side representing fish. Alligators hunt for the fish with the larger number, so whichever direction their mouths are open they are searching for the bigger fish.

Reference: https://blog.prepscholar.com/hs-fs/hubfs/body_alligator.png?width=900&name=body_alligator.png
In the example, we see the numbers 4 and 3, the alligator’s mouth places towards the left (4). So mathematically, we can show it as 4 > 3.

References: https://blog.prepscholar.com/hs-fs/hubfs/body_alligator2.png?width=900&name=body_alligator2.png
This also works the other way around. In this case, the alligator’s mouth faces right, as does the less-than sign.
In the example, we see the numbers 5 and 8, the alligator’s mouth places towards the right (8). So mathematically, we can show it as 5 < 8.
- L Method
In this method, “less than” is represented by the symbol that most resembles the letter L — it is the symbol used to denote “less than.”
The < sign looks more like an L than the > sign, so < means “less than.” Since > doesn’t look like an L, it cannot be denoted by “less than.”
Comparison of Integers
Numbers that contain both positive and negative digits, as well as zero, are called integers. The values on the number line increase as we move to the right, and decrease as we move to the left, as already shown in the illustration above.
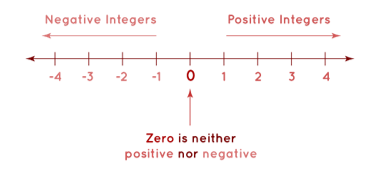
Reference: https://d138zd1ktt9iqe.cloudfront.net/media/seo_landing_files/integer-number-line-1621880568.png
We know that zero is in the middle of the number line. Positive numbers are to the right of the zero, and negative numbers are to the left of the zero.
The number at the extreme right of the number line is the greatest, and the number at the extreme left is the smallest.
Below are some conclusions which are drawn from the integers on a number line:
- A positive number is always greater than a negative number.
- The value of any negative integer is less than that of any positive integer.
- As compared to all negative integers, zero is the greater number.
- Zero is the least number among all positive integers.
Comparison of Decimal Numbers
A decimal number has both a whole number part and a decimal part. Decimal numbers with a greater whole part, therefore, have more value.
Example: When comparing 2.34 and 1.23, 2.34 is the larger number since it has a greater whole number part (2>1).
In another way, we must compare the most significant decimal numbers in order to compare the given decimal numbers. A decimal’s most significant digit is the first digit other than zero. Consider the following examples:
The most significant digit has the value 7 → 7.273
The most significant digit has the value 20 → 26.85
The most significant digit has the value 0.4 → 0.49
The most significant digit has the value 0.08 → 0.083
Therefore, a decimal like 0.7 is greater than 0.65, since the most significant digit is worth more (7>6).
Comparisons of Fractions
Step 1) Take the two fractions and convert them into decimals by dividing the numerator by the denominator.
Step 2) Compare both the decimals to see which is bigger.
Example:
Which is bigger, 3/7 or 2/5?
1) Change both fractions into decimals:
3/7 = 3 ÷ 7 = 0.43
2/5 = 2 ÷ 5 = 0.4
2) Compare the decimals:
0.43 > 0.4
Therefore, 3/7 is greater than ⅖.
Comparison with Ratios
Ratios let you compare quantities, but they do not tell you their actual values by themselves.
Comparing quantities via a ratio is different from subtracting amounts to find the difference because a ratio refers to how much one quantity is for a given amount of the other quantity.
There are two steps to be remembered while comparing ratios.
The first step is to make the consequent of both ratios equal by finding the Least Common Multiple(LCM). As soon as you have determined the LCM, divide it by both the consequent of the ratio. Finally, multiply the antecedent and consequent of the two ratios with the quotient obtained before.
Next, compare the 1st number i.e. the antecedent of both the ratios with each other. Once step 1 is done, then we move forward to step 2 to find out the comparison between the two ratios.
Example: Compare the ratios of the given quantities 2:6 and 5:4. Which of the ratios is greater?
Find the LCM of both the consequents in the ratios, namely 6 and 4. LCM of 6 and 4 is 12
Once the LCM is determined, divide it with both the numbers i.e. 12 ÷ 6 = 2 and 12 ÷ 4 = 3
Therefore, (2 x 2 ): (6 x 2) = 4 and 12 (5 x 3) : (4 x 3) = 15 and 12
Since 15 > 4, the ratio 5:4 is greater than 2:6
Compare problems in number and measurement
Compare problems involve comparisons (differences). Number comparisons are between disjoint sets (groups of objects), whereas measurements are between quantities (for example, lengths).
- Comparing sets: Number
There are 18 teachers and 25 students.
How many more students are there than teachers?
This problem involves two separate groups (teachers and students), it does not involve action (the groups are not joining or splitting), and it concerns “how many more” (a comparison).
A comparison problem can be modeled using two bars:

Using the model, we can see that there are two possible ways to find a solution:
25 – 18 = ? which is 7
18 + ? = 25 which is
- Comparing quantities: Measurement
To make comparisons, measurements can be used. Take this pencil for instance. The length is different.
This problem is structurally identical to the student and teacher problem, as can be seen from the visual models. The difference can be found in two ways:
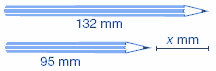
- Subtracting one length from the other when measuring each pencil
- Comparing the two lengths of the pencils by lining them up at one end.
What Are the Benefits Of Comparing And Ordering?
Comparing and ordering have the following benefits and achievements:
- It allows children to classify objects according to their size, shape, weight, and value.
- It develops children’s logical reasoning skills and aptitude.
- They are able to understand the daily challenges they face when choosing items during shopping.
- Their decision-making is strengthened as a result.
- It allows qualitative sorting among kids.
- Children develop a strong numerical sense which helps them build strong mathematical concepts.
Examples of Comparison
Example 1: Find the least four-digit number and the greatest three-digit number. Show the greater number by using the Mathematical symbol.
Answer:
We know that the least four-digit number is 1000.
999 is the greatest three-digit number.
We know, numbers with more digits are greater.
Therefore, 1000 is the greater number.
Mathematically, it can be written as follows:
So, 1000>999.
Example 2: Put the correct sign of comparison:
3 □ 5
988 □ 987
765 □ 765
Answer:
3 < 5
988 > 987
765 = 765
Example 3: Compare 71.92 and 71.9. Find the greater and least number among them.
Answer:
Numbers 71.92 and 71.90 contain the same whole number (71).
In both cases, the decimal number at the tenths place (9) is the same.
Comparing, the hundredth place digit 2 is greater than 0.
Therefore, 71.92 is greater than 71.9.
71.92 > 71.9
71.92 is the greater number, and 71.9 is the least number.
Example 4: Chris has 3kg of apples, and Nathan has 5kg of oranges. Compare their weights and find out who has a large number/ quantity of fruits?
Answer:
Given, Chris has 3 kg of apples, and Nathan has 5 kg of oranges.
Comparing their weights, we can say that 5 is larger than 3.
5kg > 3kg
Hence, Nathan has more fruits.
Conclusion
In Mathematics, the compare function is used to determine which number is greater, or lesser, or equal to another. It is an essential concept that early learners must understand to move into advanced study of the subject.
References
- https://blog.prepscholar.com/greater-than-sign-less-than-sign
- https://www.cuemath.com/numbers/comparing-and-ordering/
Recommended Worksheets
Comparing Data Using “Less” and “More” 1st Grade Math Worksheets
Comparing Lengths of Two Objects 1st Grade Math Worksheets
Comparing 2-digit Numbers Using Symbols 1st Grade Math Worksheets









