Home » Math Theory » Numbers » Performing Operations Involving Scientific Notations

Performing Operations Involving Scientific Notations

Introduction

We are familiar with natural numbers, whole numbers, decimals, fractions and other sets of numbers. But, what are scientific notations and how to perform operations involving scientific notations? Let us find out.

What are Scientific Notations?

A scientific notation is a form of writing a given number, an equation, or an expression in a form that follows certain rules. In other words, scientific notations is the standard way to express a number as the product of a real number and power of 10.

How do we define scientific notation in mathematical form?

Now that we know about the basic definition of the scientific notation, let us move to understand the mathematical definition of a scientific notation. 

Scientific notation is defined as a standardized way to represent any number as the product of a real number and a power of 10. This means that in a scientific notation, a number is written in the form of a x 10 b where a is called the coefficient and b is the exponent.

Let us understand this by an example.

Suppose we have a number 70.

We multiply it by 10 to get 700.

We again multiply 700 by 10 to get 7000

Next, we again multiply 7000 by 10 to get 70000.

We can see that the number is getting larger and larger as we keep on multiplying it by 10.

Instead of writing this number in the larger number format, we can write it down as 

70 = 7 x 10 = 7 x 10 1

700 = 7 x 100 = 7 x 10 2

7000 = 7 x 1000 = 7 x 10 3

70000 = 7 x 10000 = 7 x 10 4  

In the above four examples, 7 is the coefficient and 1, 2, 3 and 4 are the exponents respectively. 

Coefficient and Mantissa in a scientific Notation

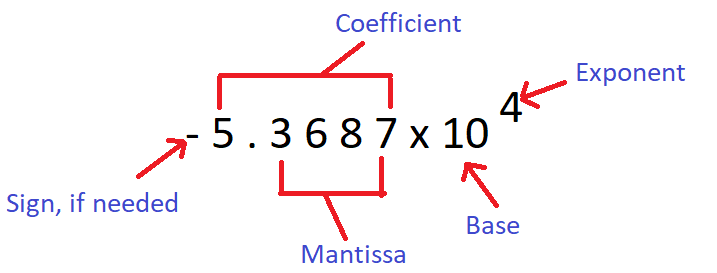
In a scientific notation, the coefficient is defined as an integer (except zero) to the left of a decimal point plus a mantissa. A mantissa is defined as the significant digits to the right of the decimal point. Let us understand this by an example. 

Suppose we have the number – 5 3 6 8 7. This number in scientific notation can be written as 

– 5 3 6 8 7 = – 5 . 3 6 8 7 x10 4 

In the above scientific notation, 

5.3687 is the coefficient while 3687 is the mantissa.

Also, 10 is the base and 4 is the exponent. We have,

Positive and Negative Exponents in Scientific Notations

Let us now discuss about the different cases of positive and negative exponents in scientific notations.

  1. When the scientific notation of any large numbers is expressed, then we use positive exponents for base 10. For example, if we have the number 7000000, it can be written as 7 x 10 6, where 6 is the positive exponent.
  2. When the scientific notation of any small numbers is expressed, then we use negative exponents for base 10. For example, if we have the decimal number 0.00003, it can be written as 3 x 10 -5, where -5 is the negative exponent.

Now, let us move ahead to learn about performing operations involving scientific notations.

General Rules for Writing of numbers in Scientific Notations

Below are some general rules that are used to write numbers in scientific notations – 

  1. The base is always 10.
  2. The exponent is a non-zero integer.
  3. The absolute value of the coefficient is greater than or equal to 1 and less than 10. 
  4. The mantissa carries the rest of the significant digits.

How to perform Arithmetic Operations Involving Scientific Notations

We are now aware of the basic definition of scientific notations and how to write in proper form. Let us learn about performing arithmetic operations involving scientific notations. We can add, subtract, multiply, and divide numbers that are written in scientific notation while still keeping the numbers in scientific notation. Let us see how.

Addition of Numbers in Scientific Notations

The following steps are involved for the addition of numbers in scientific notations – 

  1. Rewrite the number with the smaller exponent so that it has the same exponent as the number with the larger exponent by moving the decimal point of its decimal number.
  2. Add the decimal numbers. The power of 10 will not change.
  3. Convert your result to scientific notation if necessary.

Let us understand the above steps using an example.

Example

Suppose we have two numbers 7 . 3  x 10 4 and 2 . 4 8  x 10 5

We want to find the sum of these numbers. Let us see how it can be done.

Solution

Following the steps above, we will first rewrite the number with the smaller exponent so that it has the same exponent as the number with the larger exponent by moving the decimal point of its decimal number. Here, the number with the smaller exponent is 7 . 3  x 10 4 . We will have to rewrite it as a number with exponent 5. Therefore, we will increase the exponent by 1, and move the decimal point one space to the left. We will then have, the number 7 . 3  x 10 4 be rewritten 0 . 7 3  x 10 5

Now, we can see that both the numbers have the same exponents. This completes our first step. 

Now, we will move to the next steps where we need to add the decimal numbers. Remember that the power of 10 will not change.

Therefore, we will have, ( 0 . 7 3  x 10 5 ) + (2 . 4 8  x 10 5 )

 = ( 0. 7 3 + 2 . 4 8 ) x 10 5

= 3 . 2 1  x 10 5

Last, check to make sure that our answer is in scientific notation. We have 3 . 2 1 which is at least 1, but less than 10. So our answer is in scientific notation.

Subtraction of Numbers in Scientific Notations

The following steps are involved for the subtraction of numbers in scientific notations – 

  1. Rewrite the number with the smaller exponent so that it has the same exponent as the number with the larger exponent by moving the decimal point of its decimal number.
  2. Subtract the decimal numbers. The power of 10 will not change.
  3. Convert your result to scientific notation if necessary.

Let us understand the above steps using an example.

Example

Suppose we have two numbers 4 . 9 x 10 3 and 1 . 3 x 10 4

We want to subtract the second number from the first number. Let us see how it can be done.

Solution

We have been given two numbers 4 . 9 x 10 3 and 1 . 3 x 10 4 and we need to subtract the second number from the first number. This means we need to find the value of

( 4 . 9 x 10 3  ) – (1 . 3 x 10 4 )

Following the steps defined above, we will first rewrite the number with the smaller exponent so that it has the same exponent as the number with the larger exponent by moving the decimal point of its decimal number. Here, the number with the smaller exponent is 4 . 9 x 10 3  . We will have to rewrite it as a number with exponent 4. Therefore, we will increase the exponent by 1, and move the decimal point one space to the left. We will then have, the number 4 . 9 x 10 3 be rewritten 0 . 4 9 x 10 4  

Now, we can see that both the numbers have the same exponents. This completes our first step. 

Now, we will move to the next steps where we need to find the difference of the decimal numbers. Remember that the power of 10 will not change.

Therefore, we will have, ( 4 . 9 x 10 3  ) – (1 . 3 x 10 4 )

= ( 0 . 4 9 x 10 4  ) – (1 . 3 x 10 4 )

= ( 0 . 4 9 – 1 . 3 ) x 10 4

= – 0 . 8 1 x 10 4

Last, check to make sure that our answer is in scientific notation. We have 0 . 8 1 which is less than 1. Therefore, we will multiply the coefficient by 10 and reduce the exponent by 1 to get,

– 0 . 8 1 x 10 4 = – 8 . 1 x 10 3

Now, we have 8 . 1 which is at least 1 and less than 10. Hence our result is in scientific notation. 

Therefore, ( 4 . 9 x 10 3  ) – (1 . 3 x 10 4 ) = – 8 . 1 x 10 3

Multiplication of Numbers in Scientific Notations

Multiplication of numbers in scientific notation is different from their addition and subtraction. The following steps are involved for the multiplication of numbers in scientific notations – 

  1. Obtain the decimal numbers in scientific notation.
  2. Multiply the decimal numbers.
  3. Multiply the powers of 10 by adding their exponents.
  4. Convert your answer to scientific notation if necessary.

Let us understand the above steps using an example.

Example

Suppose we have two numbers ( 3 . 4  x  10 – 2 ) and ( 6 . 2 x 10 6 ) and we want to find their product. 

Solution

We have been given two numbers ( 3 . 4  x  10 – 2 ) and ( 6 . 2 x 10 6 ) and we want to find their product. This means we need to find ( 3 . 4  x  10 – 2 ) x ( 6 . 2 x 10 6 ).

Going by the above defined steps, we need to first find the product of the decimal numbers in the scientific notation.  We will have,

3 . 4  x 6 . 2 = 2 1 . 0 8  …………………………. ( 1 )

Next, we will multiply the powers of 10 for which we need to add the exponents of the two decimal numbers.

10 – 2 x 10 6 = 10 – 2 + 6  = 10 4 ………………………….. ( 2 )

Now, we will combine the results obtained in ( 1 ) and ( 2 ) to get,

( 3 . 4  x  10 – 2 ) x ( 6 . 2 x 10 6 )  = 2 1 . 0 8 x 10 4

Finally, we will convert our result in scientific notation.  We can see that we have 2 1 . 0 8 in our result which is greater than 1 and we know that for a number to be in scientific notation,  its decimal number is at least 1 but less than 10. Therefore, we will move its decimal point one space to the left. Then, to keep the overall value the same, increase the exponent on the 10 by 1. We will then have,

2 1 . 0 8 x 10 4 = 2 . 1 0 8 x 10 5

Hence, ( 3 . 4  x  10 – 2 ) x ( 6 . 2 x 10 6 ) = 2 . 1 0 8 x 10 5

Division of Numbers in Scientific Notations

The division of numbers in scientific notation is similar to their multiplication but different from their addition and subtraction. The following steps are involved for the division of numbers in scientific notations – 

  1. Obtain the decimal numbers in scientific notation.
  2. Divide the decimal numbers.
  3. Divide the powers of 10 by subtracting their exponents.
  4. Convert your answer to scientific notation if necessary.

Let us understand the above steps using an example.

Example

Suppose we have two numbers ( 8 . 4  x  10 5 ) and ( 1 . 4 x 10 – 2  ) and we want to divide the first number by the second.  

Solution

We have been given two numbers ( 8 . 4  x  10 5 ) and ( 1 . 4 x 10 – 2  ) and we want to divide the first number by the second.  This means we need to find ( 3 . 4  x  10 – 2 ) ÷ ( 6 . 2 x 10 6 ).

Going by the above defined steps, we need to first divide the decimal numbers in the scientific notation.  We will have,

8 . 4 ÷ 1 . 4 = 6 ………………….. ( 1 )

Next, we will divide the powers of 10 for which we need to subtract the exponents of the two decimal numbers. We will have,

( 10 5 ) ÷ ( 10 – 2 ) = 10 ( 5 – ( – 2 ) = 10 5 + 2 = 10 7 …………………………. ( 2 )

Now, we will combine the results obtained in ( 1 ) and ( 2 ) to get,

( 3 . 4  x  10 – 2 ) ÷ ( 6 . 2 x 10 6 ) = 6 x 10 7

Finally, we will convert our result in scientific notation.  We know that for a number to be in scientific notation,  its decimal number is at least 1 but less than 10 and in our result, we have 6 in our result which is greater than 1 and less than 10. Therefore, our result is in scientific notation. Hence,

( 3 . 4  x  10 – 2 ) ÷ ( 6 . 2 x 10 6 ) = 6 x 10 7

Rules for performing Operations involving Scientific Notations

The rules pertaining to the operation of numbers in scientific notation can be summarised as 

  1. If the given number is multiples of 10 then the decimal point has to move to the left, and the power of 10 will be positive. For example 7000 can be written as 7 × 10 3 is in scientific notation.
  2. If the given number is smaller than 1, then the decimal point has to move to the right, so the power of 10 will be negative. For example the decimal number 0.0009 can be written as 9 × 0.0001 = 9 × 10 -4 is in scientific notation.

Key Facts and Summary

  1. A scientific notation is a form of writing a given number, an equation, or an expression in a form that follows certain rules.
  2. In a scientific notation, a number is written in the form of a x 10 b where a is called the coefficient and b is the exponent.
  3. The coefficient is defined as an integer (except zero) to the left of a decimal point plus a mantissa. A mantissa is defined as the significant digits to the right of the decimal point.
  4. If the given number is multiples of 10 then the decimal point has to move to the left, and the power of 10 will be positive.
  5. If the given number is smaller than 1, then the decimal point has to move to the right, so the power of 10 will be negative.
  6. When the scientific notation of any large numbers is expressed, then we use positive exponents for base 10.
  7. When the scientific notation of any small numbers is expressed, then we use negative exponents for base 10.

Understanding Decimal Notations 4th Grade Math Worksheets
Multiplying and Dividing Numbers by Power of 10 5th Grade Math Worksheets
Rounding Whole Numbers (Tens and Hundreds) (Sea Animals Themed) Worksheets

Browse All Worksheets

Link/Reference Us

We spend a lot of time researching and compiling the information on this site. If you find this useful in your research, please use the tool below to properly link to or reference Helping with Math as the source. We appreciate your support!

  • "Performing Operations Involving Scientific Notations". Helping with Math. Accessed on April 16, 2024. https://helpingwithmath.com/performing-operations-involving-scientific-notations/.

  • "Performing Operations Involving Scientific Notations". Helping with Math, https://helpingwithmath.com/performing-operations-involving-scientific-notations/. Accessed 16 April, 2024.

  • Performing Operations Involving Scientific Notations. Helping with Math. Retrieved from https://helpingwithmath.com/performing-operations-involving-scientific-notations/.