Octahedron

Introduction

Welcome to the fascinating world of geometry! Don’t be intimidated by this enormous word; it comes from the Greek words “Octa,” which means “eight,” and “Hedra,” which means face. Today, we’ll examine a three-dimensional structure called an “Octahedron.” So an octahedron is a three-dimensional shape with eight faces. It is a member of the family of the five platonic solids. That certainly sounds intriguing. Let’s examine the specifics and discover where to use this shape daily.

Grade Appropriateness

The age range for this topic is best suited to students in grades 5 through 8—typically between 10 and 14 years old. Everyone motivated to learn and investigate geometry is invited to join the journey!

Math Domain

An octahedron falls within the domain of Geometry. Specifically, it is part of studying three-dimensional (3D) shapes or solids.

Applicable Common Core Standards

Studying the octahedron can help you meet the following Common Core Standards for Mathematics:

5.G.B.3: Understand that attributes belonging to a category of two-dimensional figures also belong to all subcategories of that category.

6.G.A.4: Represent three-dimensional figures using nets made up of rectangles and triangles, and use the nets to find the surface area of these figures.

Definition of Octahedron

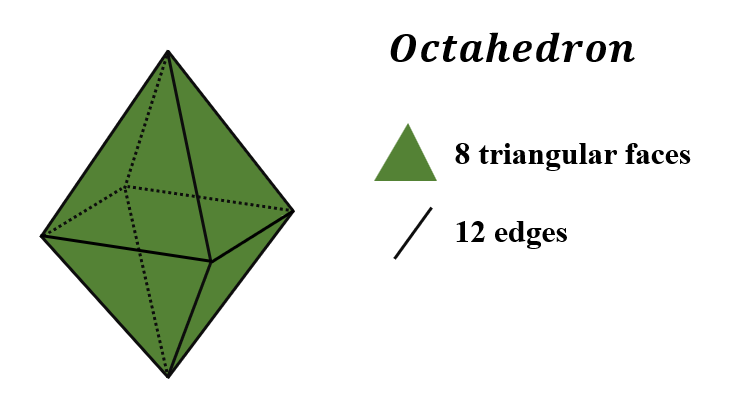
An octahedron is a polyhedron – a 3D shape with flat faces – with eight faces, all triangles. It also has 12 edges and six vertices (corners). Each vertex is the meeting point of four triangular faces. Octahedron belongs to the family of five platonic solids.

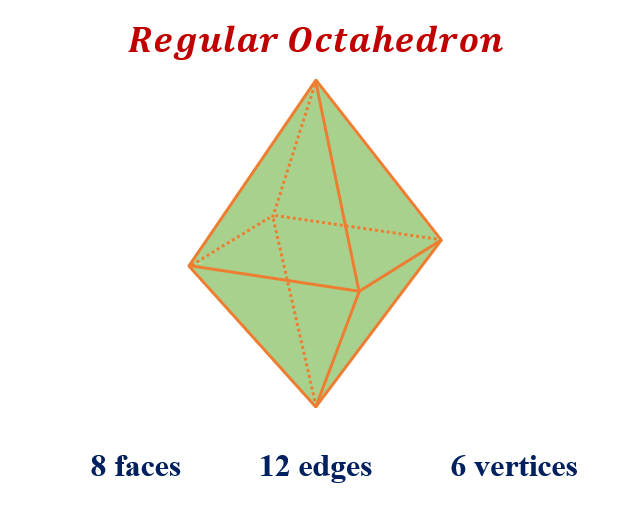
Key Concepts

Regular Octahedron: A regular octahedron is a particular type of octahedron where all the faces are equilateral triangles. In a regular octahedron, all edges are of equal length, and all angles between the edges are equal.

The volume of an octahedron: The formula to calculate the volume of a regular octahedron is: 

Volume_{Regular Octahedron}=$\frac{\sqrt{2}}{3}$ (Edge length)³.

The surface area of an octahedron: The formula to find the surface area of a regular octahedron is:

Surface Area_{Regular Octahedron}=$2\sqrt{3}$ (Edge length)².

Discussion with Illustrative Examples

An octahedron is a polyhedron that has eight faces, twelve edges, and six vertices. A regular octahedron belongs to the family of five platonic solids with faces that are all congruent equilateral triangles. 

The regular octahedron can be decomposed into two square pyramids, as shown below. 

Parts and Properties of a Regular Octahedron

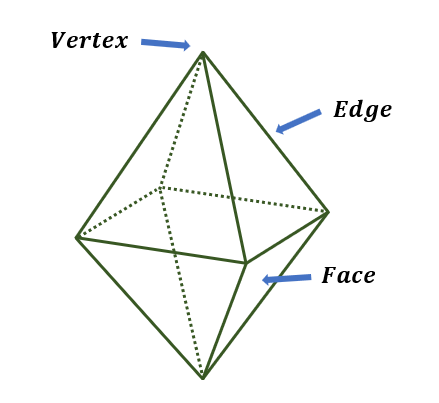
Face: An octahedron has eight faces, all in the shape of equilateral triangles. These eight faces are where the solid gets its name. ‘Octa’ means eight. These faces form the surface area of the octahedron. The square that is the base of the octahedron is not part of the surface area; therefore, the base isn’t also a face. 

Edge: When two faces touch, the formed line segment is called an edge. An octahedron consists of 12 edges.

Vertex: An octahedron consists of 6 vertices, and each vertex is formed when four edges intersect.

Base: An octahedron has a square-shaped base. If you picture an octahedron as two congruent square pyramids with their bottoms touching, then the base of the octahedron is the square between the two pyramids. 

Below is an example of a regular octahedron.

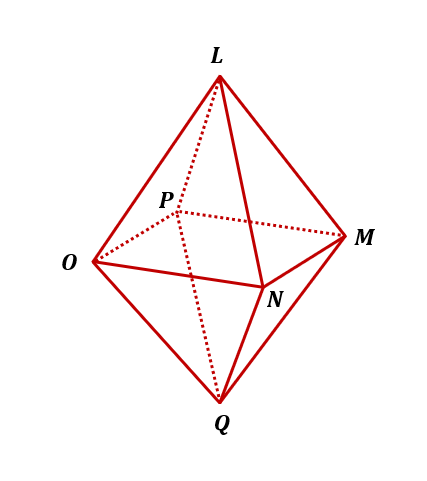
Corners L, M, N, O, P, and Q are the six vertices.

Segments LM, LN, LO, LP, QM, QN, QO, QP, NM, NO, PO, and PM are the twelve edges. 

Triangles LMN, LNO, LOP, LMP, QMN, QNO, QOP, and QMP are the eight triangular faces. 

Square MNOP is the square base of the octahedron.

Formulas Involving Octahedron

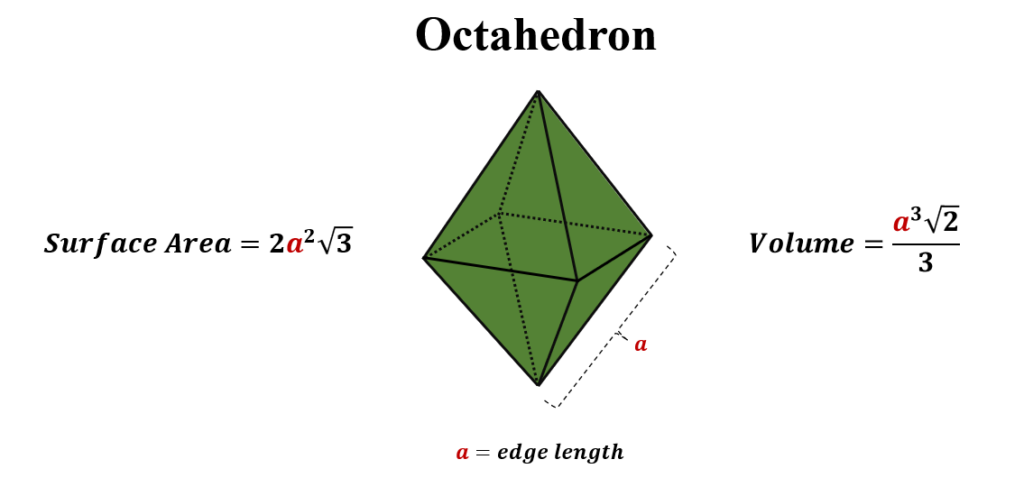
Total Surface Area of Octahedron

As seen below, a 2-D geometric net can be used to depict the surface area of an octahedron.

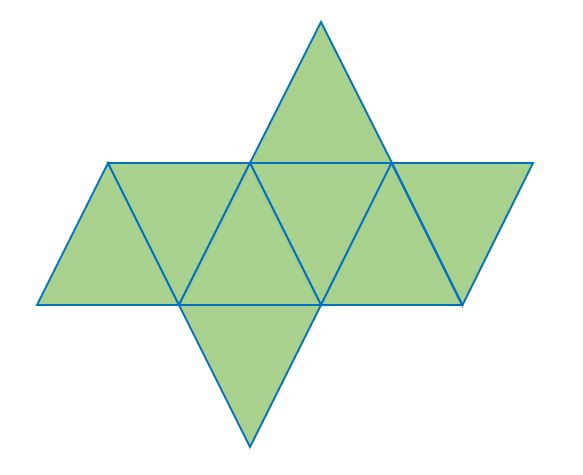
In finding the area of an equilateral triangle, we use the formula A=$\frac{\sqrt{3}}{4}$ a², where a is the side length. Since each edge of a regular octahedron is also equal to the side length of the equilateral triangle, we can calculate the total surface area of a regular octahedron by multiplying the area of one triangle by eight. Thus, we have,

Surface Area=8×$\frac{\sqrt{3}}{4}$ a²

Surface Area=2√3 a²

Surface Area=2a² √3

Volume of Octahedron

The formula for getting the volume of a regular octahedron is:

Volume=$\frac{\sqrt{2}}{3}$ a³

Volume=$\frac{a^3\sqrt{2}}{3}$

wherein a is the length of the edge of the octahedron.

Now that we know the different formulas let us try applying them. Let us say we have an octahedron whose edge length is 2 inches. What is its volume and surface area?

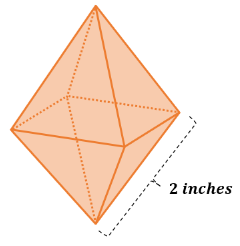Total Surface Area a=2 inches Formula: SA=2a2√3 Substitution: SA=2(2 inches)2√3 Simplify: SA≈13.86 in2	Volume a=2 inches Formula: V=$\frac{a^3\sqrt{2}}{3}$ Substitution: V=$\frac{(2)^3\sqrt{2}}{3}$ Simplify: V≈3.77 in3

Therefore, a regular octahedron’s total surface area and volume with an edge length of 2 inches are 13.86 in² and 3.77 in³, respectively.

Examples with Solution

Example 1

What is the volume and surface area if you have a regular octahedron with an edge length of 6 cm?

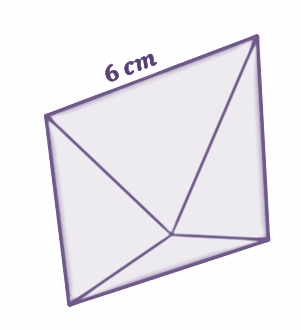
Solution

Substitute the edge length, a =6 cm, into the formula.

The volume of the Octahedron Volume=$\frac{a^3\sqrt{2}}{3}$ Volume=$\frac{(6)^3\sqrt{2}}{3}$ Volume=$\frac{216\sqrt{2}}{3}$ Volume=72√3≈101.82 cm3

Total Surface Area of the Octahedron SA=2a2√3 SA=2(6)2√3 SA=72√3≈124.71 cm2

Thus, the volume of a regular octahedron with an edge length of 6 cm is approximately 101.82 cm^3, while its total surface area is 124.71 cm².

Example 2

A dice shaped like a regular octahedron has a side length of 1.5 inches. Calculate its total surface area and volume.

Solution

Substituting the side length, a =1.5 inches, into the formula, we have,

Total Surface Area of the Dice SA=2a2√3 SA=2(1.5)2√3 SA=$\frac{9\sqrt{3}}{2}$≈7.79 in2

The Volume of the Dice Volume=$\frac{a^3\sqrt{2}}{3}$ Volume=$\frac{(1.5)^3\sqrt{2}}{3}$ Volume=$\frac{3.375\sqrt{2}}{3}$ Volume=$\frac{9\sqrt{2}}{8}$≈1.59 in3

Thus, the surface area of the dice with a side length of 1.5 inches is 7.79 in² while its volume is 1.59 in³.

Example 3

Find the volume of a regular octahedron if its total surface area is 128√3 square units.

Solution

We can find the edge length of the octahedron by substituting the given value into the formula.

2a²√3=128√3 (Substitution)

a²=$\frac{128\sqrt{3}}{2\sqrt{3}}$ (Dividing both sides by  2√3)

a²=64 (Simplify)

a=8 units

Let us now substitute the edge length, a, into the volume formula.

V=$\frac{a^3\sqrt{2}}{3}$

V=$\frac{(8)^3\sqrt{2}}{3}$

V=$\frac{512\sqrt{2}}{3}$

V≈241.36 cubic units

Hence, the volume of a regular octahedron is approximately 241.36 cubic units if it has a total surface area of 128√3 square units.

Real-life Application with Solution

Problem 1

Olivia has a pair of diamond earrings shaped like an octahedron, and its edge length is 1 cm. What would be its volume and surface area?

Solution

Volume=$\frac{(1)^3\sqrt{2}}{3}$

Volume=$\frac{\sqrt{2}}{3}$

Volume≈0.47 cm³

Surface Area=2(1)² √3

Surface Area=2√3≈3.46 cm²

Hence, Olivia’s earring’s volume and surface area are 0.47 cm³ and 3.46 cm², respectively.

Problem 2

William used metal wire with a total length of 108 inches to form an octahedron. Find its edge length, surface area, and volume.

Solution

Since the length of the wire is 108 inches, we can calculate the edge length by dividing it by 12. Remember that a regular octahedron has 12 edges. Thus,

a=$\frac{108 inches}{12}$=9 inches

Let us now substitute the calculated edge length, a, into the formulas.

Total Surface Area of the Octahedron SA=2a2√3 SA=2(9)2 √3 SA=163√3 SA≈280.59 in2

The volume of the Octahedron Volume=$\frac{a^3\sqrt{2}}{3}$ Volume=$\frac{(9)^3\sqrt{2}}{3}$ Volume=$\frac{729\sqrt{2}}{3}$ Volume=$243\sqrt{2}$ Volume≈343.65 in3

Practice Test

Answer each problem. Express your answer with the correct units.

1. Calculate the volume of a regular octahedron with an edge length of 3 cm.

2. Calculate the surface area of a regular octahedron with an edge length of 4 cm.

3. What is the edge length if a gemstone cut as an octahedron has a surface area of 24√3 cm²?

4. Find the edge length of a regular octahedron-shaped toy block with a volume of √(50/3) cm³.

Answers:

1. Since side length  a=3 cm, we have,

Volume=$\frac{(3)^3√2}{3}$=9√2 ≈ 12.73 cm²

2. With an edge length of 4 cm,

Surface Area=2(4)² √3=32√3 ≈ 55.43 cm².

3. Given that the surface area is 24√3 cm²,

2a²√3=24√3

a²=$\frac{24\sqrt{3}}{2\sqrt{3}}$

a²=12

a=√12 ≈ 3.46 cm

4. With the given volume of 503 cm³, we have,

a323=503

a3=502

a3=5

a=351.71 cm

Frequently Asked Questions (FAQs)

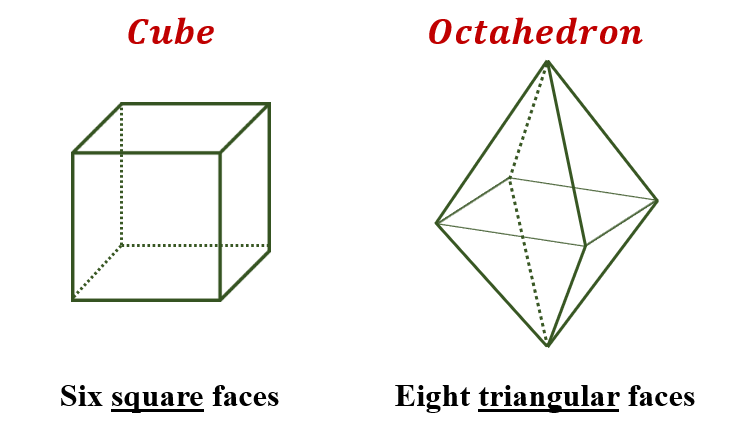
What is the difference between a cube and an octahedron?

A cube has six faces, all of which are squares, while an octahedron has eight faces, all of which are triangles.

What are some examples of octahedrons in real life?

Some examples of octahedrons in real life include board game dice, minerals like diamonds, some decorative pieces, a Rubik’s cube, some ornaments like earrings, and certain types of kites that can be shaped like an octahedron.

Are all the faces of an octahedron the same?

In a regular octahedron, yes, all faces are equilateral triangles. The image below shows a geometric net with eight equilateral triangles that form a regular octahedron.

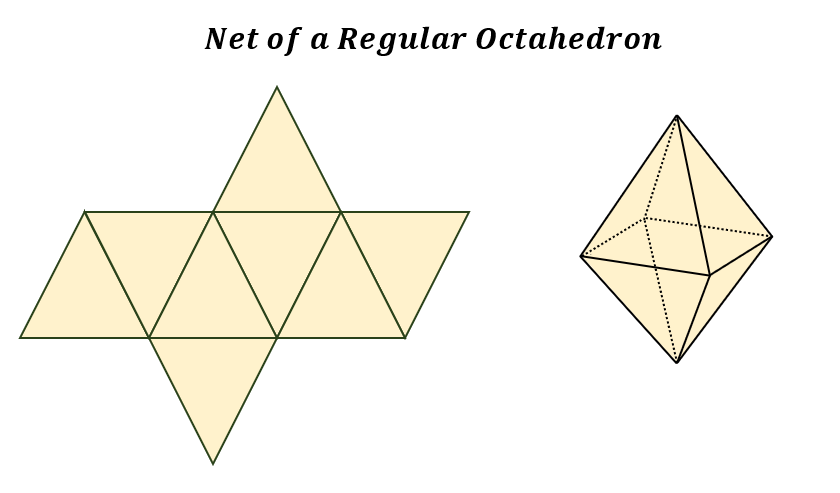
How many edges does an octahedron have?

An octahedron has twelve edges. The line segment created when two octahedron faces touch is called an edge.

Can an octahedron have more than eight faces?

No, by definition, an octahedron always has eight faces. If it has more or fewer, it would be a different type of polyhedron.

Recommended Worksheets

Octahedron (National Hispanic Heritage Month Themed) Math Worksheets
Platonic Solids (Earth Day Themed) Math Worksheets
Icosahedron (Holi Themed) Math Worksheets