Introduction
Square numbers are the product when a number is multiplied by itself. Because of this, they are always positive! There is a lot to learn about square numbers, and these are just a few.
In this article, we will define square numbers, examine what makes a number a “square number,” explore more impressive facts about square numbers and utilize formulas to add square numbers.
What is a square number?
Definition
A square number commonly referred to as a perfect square, is created by multiplying a number by itself. In other words, the product of a number multiplied by itself is a square number.
For example, for a variable n, the notation for a square of a number n is n2, usually read as n squared. An index or power (2) is used as another way of writing square numbers. Hence, 16 is a square number since it equals 42 and can be written as 4×4.
Here is a list below shows the first 30 square numbers expressed as n×n and n2
| n | n × n | n2 | Square Numbers |
| 1 | 1 × 1 | 12 | 1 |
| 2 | 2 × 2 | 22 | 4 |
| 3 | 3 × 3 | 32 | 9 |
| 4 | 4 × 4 | 42 | 16 |
| 5 | 5 × 5 | 52 | 25 |
| 6 | 6 × 6 | 62 | 36 |
| 7 | 7 × 7 | 72 | 49 |
| 8 | 8 × 8 | 82 | 64 |
| 9 | 9 × 9 | 92 | 81 |
| 10 | 10 × 10 | 102 | 100 |
| 11 | 11 × 11 | 112 | 121 |
| 12 | 12 × 12 | 122 | 144 |
| 13 | 13 × 13 | 132 | 169 |
| 14 | 14 × 14 | 142 | 196 |
| 15 | 15 × 15 | 152 | 225 |
| 16 | 16 × 16 | 162 | 256 |
| 17 | 17 × 17 | 172 | 289 |
| 18 | 18 × 18 | 182 | 324 |
| 18 | 19 × 19 | 192 | 361 |
| 20 | 20 × 20 | 202 | 400 |
| 21 | 21 × 21 | 212 | 441 |
| 22 | 22 × 22 | 222 | 484 |
| 23 | 23 × 23 | 232 | 529 |
| 24 | 24 × 24 | 242 | 576 |
| 25 | 25 × 25 | 252 | 625 |
| 26 | 26 × 26 | 262 | 676 |
| 27 | 27 × 27 | 272 | 729 |
| 28 | 28 × 28 | 282 | 784 |
| 29 | 29 × 29 | 292 | 841 |
| 30 | 30 × 30 | 302 | 900 |
Why are they known as “square numbers”?
Square numbers are commonly referred to as perfect squares. Since squares have equal sides, determining their area is as easy as multiplying by themselves or obtaining the square of their side length.
Let us use some tiles arranged in a square to illustrate this concept.
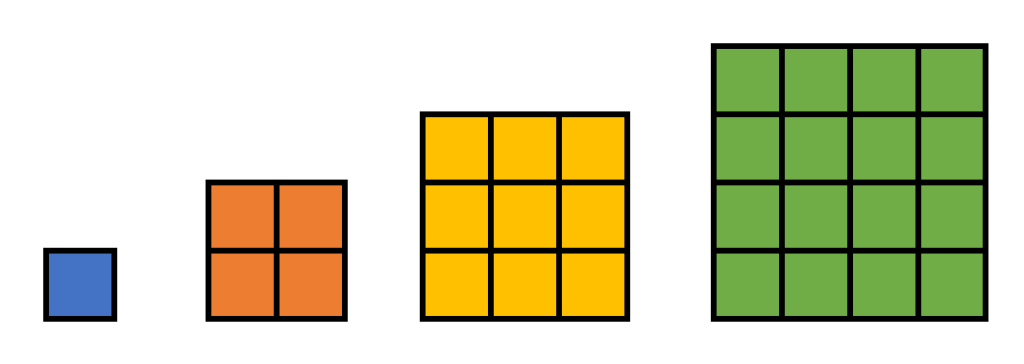
There is one (1) tile in the first square, four (4) in the second, nine (9) in the third, and sixteen (16) in the last square. Each square indicates how many rows and columns it has one row and one column for the square with one tile, two rows and two columns for the square with four tiles, three rows and three columns for the square with nine tiles, and four rows and four columns for the squares with sixteen tiles.
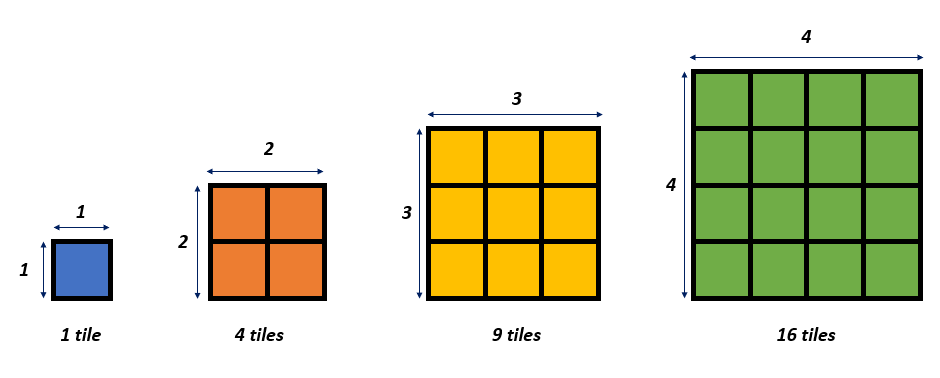
A “square number” is how many square tiles can fit into a square arrangement. Hence, we can see that 1, 4, 9 and 16 are square numbers or perfect squares.
1 × 1 = 1
2 × 2 = 4
3 × 3 = 9
4 × 4 = 16
The image below shows that if the pattern continues, these are the number of tiles to form each perfect square. So, if the pattern continues, we can have 5 × 5 = 25 and 6 × 6 = 36.

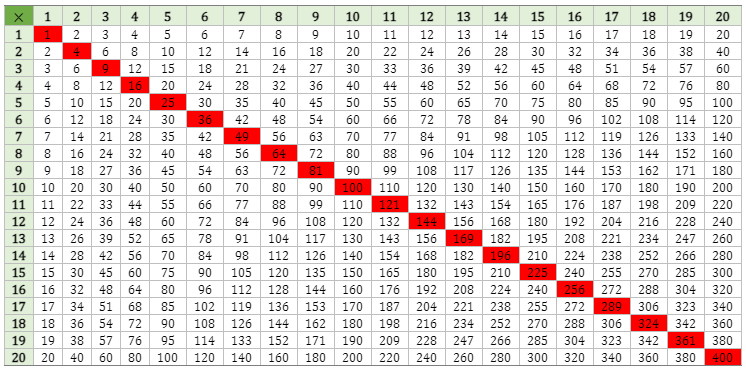
Square Numbers in the Multiplication Table Chart
The chart below shows the multiplication table chart from 1 to 20. The numbers highlighted in red are the square numbers or the product when a number is multiplied by itself.
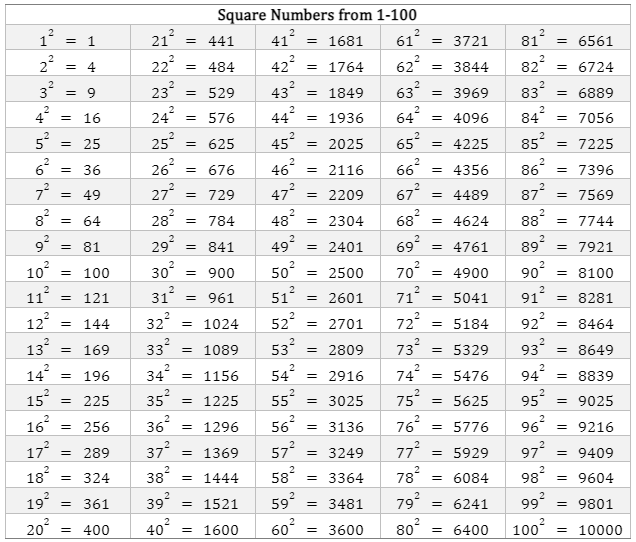
List of Square Numbers from 1-100
A number is multiplied by itself to produce a square number, often known as a perfect square. In other words, a square number results from multiplying a number by itself.
The table below shows the list of square numbers from 1 to 100.
Squares of Negative Numbers
A positive number is produced when two negative numbers are multiplied. This concept allows for the calculation of the squares of negative numbers.
The following are examples of square numbers when a negative number is multiplied by itself.
( -5 ) x ( -5 ) = ( -5 )2 = 25
( -8 ) x ( -8 ) = ( -8 )2= 64
( -10 ) x ( -10 ) = ( -10 )2= 100
( -13 ) x ( -13 ) = ( -13 )2 = 169
( -16 ) x ( -16 ) = ( -16 )2 = 256
( -19 ) x ( -19 ) = ( -19 )2 = 361
Exploring Square Numbers
There is much to learn from square numbers and their patterns. Some of the properties of square numbers include the following.
- Numbers with 2, 3, 7, or 8 at the unit place should never be square numbers.
Examples: 22, 43, 57, 88
These numbers end in either 2, 3, 7, or 8 and are not square numbers.
- Some square numbers may include the digits 0, 1, 4, 5, 6, or 9 as their last digits.
Examples: 100, 121, 324, 225, 256, and 289
These numbers have the final digits of either 0, 1, 4, 5, 6, or 9 and are square numbers.
- The squares of even numbers are even numbers, while the squares of odd numbers are odd numbers.
Examples:
64 is an even number, and it is a square of 8, which is also an even number.
81 is an odd number, and it is a square of 9, an odd number.
- The square of the numbers that have the units place in either 1 or 9 has one (1) as the last digit.
Examples:
The square of 21, a number with a unit place of 1, is 441.
The square of 39, a number with a unit place of 9, is 1521.
Both 441 and 1521 end in 1.
- If you divide a square number by 4, the remainder is either 0 or 1.
Examples:
When 144 is divided by 4, the remainder is 0.
When 81 is divided by 4, the remainder is 1.
- A number can be a square if it has an even number of zeros at the end. On the other hand, if the number of zeros is odd, then it can never be a perfect square.
Examples:
400, 1600, and 3600 are numbers that end with an even number of zeros and are perfect squares.
20, 50, 1000, and 3000 are numbers that end with an odd number of zeros and are not perfect squares.
- A square number that ends in 6 must be the result of multiplying a number that ends in 4 or 6 by itself.
Examples:
576 and 1156 are the squares of 24 and 34, respectively. These numbers end in 4, and their squares end in 6.
The square of 16 and 26 are 256 and 676, respectively. These numbers end in 6, and their squares end in 6.
- If n is the number of odd numbers, then the sum of consecutive n odd numbers is n2.
The table below shows this property.
| Consecutive odd numbers | Sum of Consecutive Odd Numbers | n Number of Odd Numbers | n2 |
| 1 | 1 | 1 | 12 = 1 |
| 1 + 3 | 4 | 2 | 22 = 4 |
| 1 + 3 + 5 | 9 | 3 | 32 = 9 |
| 1 + 3 + 5 + 7 | 16 | 4 | 42 = 16 |
| 1 + 3 + 5 + 7 + 9 | 25 | 5 | 52 = 25 |
| 1 + 3 + 5 + 7 + 9 + 11 | 36 | 6 | 62 = 36 |
| 1 + 3 + 5 + 7 + 9 + 11 + 13 | 49 | 7 | 72 = 49 |
- Finding an integer’s square root is the opposite of square numbers. Therefore, the square value of a number is achieved by multiplying it by itself. In contrast, you can get the square root of any given integer by looking for a number that shows the original value when squared.
Square Roots of Square Numbers from 1 – 900
| $\sqrt{1}$=1 | $\sqrt{121}$=11 | $\sqrt{441}$=21 |
| $\sqrt{4}$=2 | $\sqrt{144}$=12 | $\sqrt{484}$=22 |
| $\sqrt{9}$=3 | $\sqrt{169}$=13 | $\sqrt{529}$=23 |
| $\sqrt{16}$=4 | $\sqrt{196}$=14 | $\sqrt{576}$=24 |
| $\sqrt{25}$=5 | $\sqrt{225}$=15 | $\sqrt{625}$=25 |
| $\sqrt{36}$=6 | $\sqrt{256}$=16 | $\sqrt{676}$=26 |
| $\sqrt{49}$=7 | $\sqrt{289}$=17 | $\sqrt{729}$=27 |
| $\sqrt{64}$=8 | $\sqrt{324}$=18 | $\sqrt{784}$=28 |
| $\sqrt{81}$=81 | $\sqrt{361}$=19 | $\sqrt{841}$=29 |
| $\sqrt{100}$=10 | $\sqrt{400}$=20 | $\sqrt{900}$=30 |
Adding Square Numbers
The calculation of the sum of squares can be done using a variety of formulas and methods.
Formula: Sum of Squares of Two Numbers
The formula for adding the squares of two numbers is given by,
x2 + y2 = ( x+y )2 – 2xy
Let us use the formula to get the sum of the squares of the numbers below:
( a ) 5 and 6
( b ) 7 and 11
( c ) -3 and -8
Solution:
( a ) Let us say that x = 5 and y = 6. Using the formula to find the sum of 5 and 6, we have,
52 + 62 = ( 5+6 )2 – 2( 5 )( 6 )
52 + 62 = ( 11 )2 – 60
52 + 62 = 121 – 60
52 + 62 = 61
Let us also check if the left-hand side of the equation is indeed 61. So, we have,
52 + 62 = 25 + 36 = 61
( b ) Let x = 7 and y = 11. When the values are substituted to the formula, we have,
72 + 112 = ( 7+11 )2 = -2( 7 )( 11 )
72 + 112 = ( 18 )2 – 154
72 + 112 = 324 – 154
72 + 112 = 170
( c ) Let us use x = -3 and y = -8.
( -3 )2 + ( -8 )2 = ( -3+ (-8) )2 -2( -3 )( -8 )
( -3 )2 + ( -8 )2 = ( -11 )2 – 48
( -3 )2 + ( -8 )2 = 121 – 48
( -3 )2 + ( -8 )2 = 73
The solution below shows that the left-hand side of the equation is 73.
( -3 )2 + ( -8 )2 = 9 + 64 = 73
Formula: Sum of Squares of Three Numbers
The formula for adding the squares of three numbers is given by,
x2 + y2 + z2 = ( x + y + z)2 -2xy -2yz -2xz
Let us use the formula to get the sum of the squares of the following numbers:
( a ) 4, 7, 10
( b ) 5, 6, 8
( c ) -3, 2, 9
Solution:
( a ) Let us say that x = 4, y = 7 and z = 10. Substituting the given to the formula to get the sum of the squares of these numbers, we have,
42 + 72 + 102 = (4 + 7 + 10 )2 – 2( 4 )( 7 ) -2( 7 )( 10 ) -2( 4 )( 10 )
42 + 72 + 102 = ( 21 )2 -56 -140 -80
42 + 72 + 102 = 441 -56 -140 -80
42 + 72 + 102 = 165
( b )Let us have x = 5, y = 6, and z = 8 to find the sum of their squares. By substitution, we have the solution below,
52 + 62 + 82 = ( 5 + 6 + 8 )2 -2( 5 )( 6 ) -2( 6 )( 8 ) -2( 5 )( 8 )
52 + 62 + 82 = ( 19 )2 – 60 – 96 – 80
52 + 62 + 82 = 361 – 60 – 96 – 80
52 + 62 + 82 = 125
( c ) Let us say that x = -3, y = 2 and z = 9. Substituting the given to the formula to get the sum of the squares of these numbers, we have,
( -3 )2 + 22 + 92 = ( -3 + 2 + 9 )2 -2( -3 )( 2 ) -2( 2 )( 9 ) -2( -3 )( 9 )
( -3 )2 + 22 + 92 = ( 8 )2 + 12 – 36 + 54
( -3 )2 + 22 + 92 = 64 + 12 – 36 + 54
( -3 )2 + 22 + 92 = 94
Formula: Sum of first “n” square numbers
Let us say that n represents a natural number. The family of natural numbers includes all the counting numbers starting from 1 to infinity. Therefore, the sum or total of the first “n” natural numbers is expressed as $K_{k=1}^{n}$ k2 and can be calculated using the formula:
$K_{k=1}^{n}$ k2 = 12 + 22 + 32 + … + n2 = $\frac{n (n+1) ( 2n+1 )}{6}$
or we may also use,
Sn = $\frac{n (n+1) ( 2n+1 )}{6}$
Examples:
( a ) Determine the sum of the squares of the first five (5) natural numbers.
( b ) Calculate the sum of the squares of the first seven (7) natural numbers.
( c ) Determine the sum of the squares of the first ten (10) natural numbers.
Solution:
( a ) Determine the sum of the squares of the first five (5) natural numbers.
Let us use n=5 since we are asked to get the sum of the first five (5) natural numbers. Hence, we have,
S5 = $\frac{5( 5+1 )( 2⋅5+1 )}{6}$
S5 = $\frac{5 6 ( 11 )}{6}$
S5 = $\frac{330}{6}$
S5 = 55
To check this answer, let us have the squares of the first five natural numbers,
S5 = 12 + 22 + 32 + 42 + 52
S5 = 1 + 4 + 9 + 16 + 25
S5 = 55
( b ) Calculate the sum of the squares of the first seven (7) natural numbers.
Since we are asked to get the sum of the first seven (7) natural numbers, let us have n=7.
S7 = $\frac{7( 7+1 )( 2⋅7+1 )}{6}$
S7 = $\frac{7( 8 )( 15 )}{6}$
S7 = $\frac{840}{6}$
S7 = 140
Let us check this answer by getting the sum of the squares of the numbers from 1 to 7.
S7 = 12 + 22 + 32 + 42 + 52 + 62 + 72
S7 = 1 + 4 + 9 +16 + 25 + 36 + 49
S7 = 140
( c ) Determine the sum of the squares of the first ten (10) natural numbers.
To find the sum of the first ten (10) natural numbers, we have,
S10 = $\frac{10( 10+1 )( 2⋅10+1 )}{6}$
S10 = $\frac{10( 11 )( 21 )}{6}$
S10 = $\frac{2310}{6}$
S10 = 385
To check this answer, we have,
S10 = 12 + 22 + 32 + 42 + 52 + 62 + 72 + 82 + 92 + 102
S10 = 1 + 4 + 9 + 16 + 25 + 36 + 49 + 64 + 81 + 100
S10 = 385
Formula: Sum of the Squares of the first n even numbers
By applying the following formula, we can determine the sum of the squares of the first (n) even numbers:
Sn = $\frac{2n(n+1)(2n+1)}{3}$
Examples:
( a ) Determine the sum of the squares of the first eight (8) even natural numbers.
( b ) Calculate the sum of the squares of the first 15 even natural numbers.
Solution:
( a ) Determine the sum of the squares of the first eight (8) even natural numbers.
We will use n=8 since we are asked to get the sum of the squares of the first eight (8) even natural numbers.
Substituting the value of n to the formula, we have,
S8 = $\frac{(2⋅8)(8+1)(2⋅8+1)}{3}$
S8 = $\frac{(16)(9)(17)}{3}$
S8 = $\frac{2448}{3}$
S8 = 816
Let us check by getting each of the squares of the first eight (8) even natural numbers, so we have,
S8 = 22 + 42 + 62 + 82 + 102 + 122 + 142 + 162
S8 = 4 + 16 + 36 + 64 + 100 + 144 + 196 + 256
S8 = 816
( b ) Calculate the sum of the squares of the first 15 even natural numbers.
Let us use n=15 to get the sum of the squares of the first 15 even natural numbers.
Using the value of n in the formula, we have,
S15 = $\frac{(2⋅1)(15+1)(2⋅15+1)}{3}$
S15 = $\frac{(30)(16)(31)}{3}$
S15 = $\frac{14880}{3}$
S15 = 4960
Let us check by getting each of the squares of the first 15 even natural numbers, so we have,
S15 = 22 + 42 + 62 + 82 + 102 + 122 + 142 + 162 + 182 + 202 + 222 + 242 + 262 + 282 + 302
S15 = 4 +16 +36 +64 +100 +144 +196 +256+324+400 +484 +576 +676+784 +900
S15 = 4960
Formula: Sum of the Squares of the first “n” odd numbers
The following formula is used to determine the sum of the squares of the first “n” odd numbers:
Sn = $\frac{n(2n+1)(2n-1)}{3}$
Examples:
( a ) Determine the sum of the squares of the first five (5) odd natural numbers.
( b ) Calculate the sum of the squares of the first twelve (12) odd natural numbers.
Solution:
( a ) Determine the sum of the squares of the first five (5) odd natural numbers.
We will use n=5 since we are asked to get the sum of the squares of the first five (5) odd natural numbers.
Substituting the value of n to the formula, we have,
S5 = $\frac{(5)(2⋅5+1)(2⋅5-1)}{3}$
S5 = $\frac{(5)(11)(9)}{3}$
S5 = $\frac{495}{3}$
S5 = 165
Let us check by getting each of the squares of the first five (5) odd natural numbers, so we have,
S5 = 12 + 32 + 52 + 72 + 92
S5 = 1 + 9 + 25 + 49 + 81
S5 = 165
( b ) Calculate the sum of the squares of the first 12 odd natural numbers.
Let us use n=12 to get the sum of the squares of the first 12 odd natural numbers.
Using the value of n in the formula, we have,
S12 = $\frac{(12)2⋅12+1)(2⋅12-1)}{3}$
S12 = $\frac{(12)(25)(23)}{3}$
S12 = $\frac{6900}{3}$
S12 = 2300
Let us check by getting each of the squares of the first 12 odd natural numbers, so we have,
S12 = 12 + 32 + 52 + 72 + 92 + 112 + 132 + 152 + 172 + 192 + 212 + 232
S12 = 1 + 9 + 25 + 49 + 81 + 121 + 169 + 225 + 289 + 361 + 441 + 529
S12 = 2300
Summary
A square number commonly referred to as a perfect square, is created by multiplying a number by itself. In other words, the product of a number multiplied by itself is a square number.
The notation for the square of a number n is n2.
Square numbers represent the area of a square. Since squares have equal sides, determining their area is as easy as multiplying by themselves or obtaining the square of their side length.
Adding Square Numbers
Formula: Sum of Squares of Two Numbers
x2 + y2 = (x+y)2-2xy
Formula: Sum of Squares of Three Numbers
x2 + y2 +z2 = (x + y + z)2 – 2xy – 2yz – 2xz
Formula: Sum of first “n” square numbers
Sn = $\frac{n( n+1 )( 2n+1 )}{6}$
Formula: Sum of squares of the first “n” even numbers
Sn = $\frac{2n(n+1)(2n+1)}{3}$
Formula: Sum of squares of the first “n” odd numbers
Sn = $\frac{n(2n+1)(2n-1)}{3}$
Frequently Asked Questions on Square Numbers (FAQs)
What are square numbers?
A square number commonly referred to as a perfect square, is created by multiplying a number by itself. In other words, the product of a number multiplied by itself is a square number.
What are the first 10 square numbers?
From 1 to 100, there are 10 square numbers. The numbers highlighted in red below are the square numbers from 1 to 100.
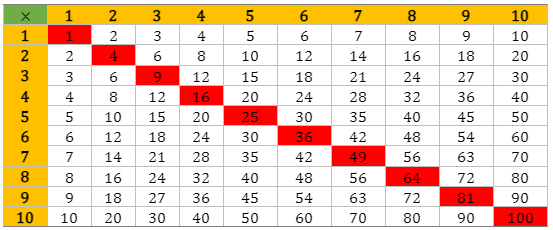
What is the difference between a square number and a square root?
The opposite of a square root is a square number. A number multiplied by itself is called a square number. The square root of a number is a number that, when multiplied by itself, gives the original number.
Square numbers use the arithmetic operator (2), while square roots use the symbol √. For example, in 62=36, 36 is the square number, while the square root of 36 (√36) is 6.
Recommended Worksheets
Square Root (Labor Day Themed) Math Worksheets
Square Numbers (International Museum Day Themed) Math Worksheets
Co-Prime Numbers (Bastille Day Themed) Math Worksheets









