Home » Math Theory » Number Sense » Prime Factorization

Prime Factorization

Introduction

Multiplication and division are two of the important operations in mathematics. We can multiply a number by any number. Similarly, a number can be divided by any number. Two important terms that are related to the multiplication and division of numbers are factors and multiples. The understanding of one of these is incomplete without studying the other. Therefore, before we move ahead and learn about factors, let us recall what we mean by multiple of a number. 

Definition of a multiple

A multiple of a whole number is the product of the number and any counting number. If we multiply 3 by 1, 2 , 3 , 4, 5 , 6 ….. we get

3 x 1 = 3

3 x 2 = 6

3 x 3 = 9

3 x 4 = 12

3 x 5 = 15

3 x 6 = 18 etc.

Thus 3, 6 , 9 , 12 , 15 , 18  and so on are the multiples of 3.

Now, let us understand the definition of factors.

Definition of a factor

A factor of a number is an exact divisor of that number. In other words, a factor of a number is that number that completely divides the number without leaving a remainder. For example, each of the numbers, 1, 2, 3, 4, 6 and 12 is a factor of 12. However, none of the numbers 5, 7, 8, 9, 10 and 11 is a factor of 12. 

Properties of Factors

Following are the properties of factors of a number – 

  1. 1 is a factor of every number. For example, 1 x 1 = 1, 4 x 1 = 4, 7 x 1 = 7 and so on
  2. Every number is a factor of itself. For example, we can write 6 as 6 x 1 = 6 which means that both 6 and 1 are the factor of the number 6. Similarly, we can write 12 as 12 x 1 = 12 which means that both 12 and 1 are the factor of the number 12.
  3. Every factor of a number is an exact divisor of the number itself. For example, the factors of the number 12 are 1, 2, 3, 4, 6 and 12. We can see that each of these factors divides 12. We can check the same for other numbers as well.
  4. Every factor of a number is less than or equal to that number. For example, if we consider the factors of 18, we will have, 1, 2, 3, 6, 9 and 18. Out of these numbers, 18 itself is the largest factor and all other factors are less than 18.
  5. Factors of a given number are finite. We have seen in the previous property that the factors are 18 are 1, 2, 3, 6, 9 and 18 and there cannot be a factor that is greater than the number 18 itself. Since the number is finite, therefore, it will have finite numbers of factors only.

Common Factors

We have now learnt about the factors as well as multiples of a number. Let us now look at the factors of more than one number. Those factors which are common among the factors of two or more numbers are known as common factors. Let us understand it through an example.

Let us consider two numbers, 12 and 18. The factors of 12 and 18 are – 

Factors of 12 are – 1, 2, 3, 4, 6 and 12

Factors of 18 are – 1, 2, 3, 6, 9 and 18.

From above, we can clearly see that 1, 2, 3 and 6 are the common factors of 12 and 18.

Let us consider another example.

Consider the numbers 9, 15 and 21. The factors of 9, 15 and 21 are – 

Factors of 9 – 1, 3 and 9

Factors of 15 – 1, 3, 5 and 15

Factors of 21 – 1, 3, 7 and 21

From above, we can clearly see that 1 and 3 are the common factors of 9, 15 and 21.

Prime Factorisation

Prime factorization is a process of factoring a number in terms of prime numbers i.e. the factors will be prime numbers. Let us understand it through an example.

Prime factorisation of 16 is 2 x 2 x 2 x 2

Prime factorisation of 27 is 3 x 3 x 3 

Prime factorisation of 24 is 2 x 2 x 2 x 3

Prime factorisation of 36 is 2 x 2 x 3 x 3

Factor Trees

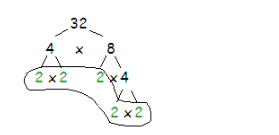
A factor tree shows the prime factors of a composite number in a “tree-like” form. Drawing factor trees is a good way of doing prime factorization. You can make different factor trees to find the same prime factorization. Look at the two examples below.

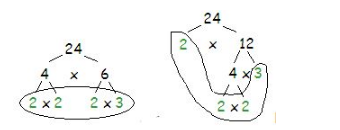
We can see from above that

Prime factorisation of 24  = 2 x 2 x 2 x 3

Similarly, Prime factorisation of 32  = 2 x 2 x 2 x 2 x 2

How to find the prime factorisation of a number ( s ) ?

Finding the prime factorisation of a number is similar to the process of finding any other factor of a number. The following steps should be followed to find the prime factorisation of a number – 

  1. Divide the given number by the smallest prime number possible.
  2. Now, check the quotient. If it is not a prime number divide this quotient by the smallest prime number possible.
  3. Repeat the previous step and check the quotient. If it is not a prime number divide this quotient by the smallest prime number possible.
  4. Repeat the above [proves until wither the quotient is 1 or it is a prime number.
  5. Multiply all the prime numbers thus obtained to find the HCF of the numbers ( if the numbers are more than 1)

Prime factorisation can be used for a number of purposes such as finding the HCF of two or more numbers. Let us learn more about it

Using Prime Factorisation to find HCF of two numbers

The highest common factor ( H. C. F. ) of two or more numbers is the greatest or the largest among common factors. In other words, the H. C. F. of two or more numbers is the largest number that divides all the given numbers exactly. 

In order to find the highest common factor ( H. C. F. ) of two or more numbers, the following steps are followed- 

  1. Obtain the numbers. 
  2. Write the prime factorisation of all the numbers.
  3. Identify the common factors.
  4. For each common prime factor find the minimum number of times it occurs in the prime factorisation of the given numbers.
  5. Multiply each common prime factor the number of times determine the previous step and find their product to get the highest common factor ( H. C. F. ) of the given numbers. 

Let us understand the above steps through an example.

Suppose we want to find the highest common factor ( H. C. F. ) of 90 and 48. We shall follow the above listed steps for this purpose.

  1. Obtain the numbers. We have the numbers as 90 and 48.
  2. Write the prime factorisation of all the numbers. We have
    90 = 2 x 3 x 3 x 5 and 48 = 2 x 2 x 2 x 2 x 3
  3. Identify the common factors. We can see from above that the common factors of 90 and 48 are 2 and 3.
  4. For each common prime factor find the minimum number of times it occurs in the prime factorisation of the given numbers. We can see that the common factor 2 appears one time in the prime factorisation of 90 while it appears 4 times in the prime factorisation of 48. Similarly, the common factor 3 appears two times in the prime factorisation of 48 while it appears one time in the prime factorisation of 48.
  5. Multiply each common prime factor the number of times determine the previous step and find their product to get the highest common factor ( H. C. F. ) of the given numbers. H. C. F. of 90 and 48 = 2 x 3 = 6

Using Prime Factorisation to find the Least Common Multiple ( LCM ) of two numbers

The least common multiple can be defined as the lowest positive integer that is multiple in a given set of numbers. We also know that if a number is a multiple of two or more numbers, it is called a common multiple of the numbers. For example, we know that

2 x 3 = 6

Therefore, 6 is a multiple of both 2 and 3. Therefore 6 is said to be a common multiple of both 2 and 3.

The Least Common Multiple ( L C M ) of two or more numbers is defined as the smallest number ( other than zero ) that is a multiple of those numbers. In other words, the least common multiple of two or more numbers is the smallest number which is divisible by all the given numbers. This means that there cannot be a number divisible by the given numbers and smaller than the least common multiple.

Let us understand this through an example.

Suppose we have two numbers, 8 and 12.

Let us check the multiples of these two numbers. We have,

Multiples of 8 = 8, 16, 24, 32, 40 , 48, 56, 64, 72 and so on…..

Multiples of 12 = 12, 24, 48, 60, 72 and so on …………

From above we can see that the common multiples of 8 and 12 are 24, 48, 72 and so on. Among these 24 is the least common multiple of these two numbers. Therefore, 12 is the least common multiple or L C M of 8 and 12.

Now, As the name suggests, the prime factorisation method involves finding the prime factors of the given numbers and then computing the least common multiple ( L C M ). In this method, the following steps are used to find the L C M  – 

  1. Obtain the given numbers.
  2. Find the prime factors of each number. 
  3. Expand each number as a product of its prime factors
  4. Find the product of all different prime factors with the highest power in the prime factorisation of each number.
  5. The number obtained in the above step is the required L C M of the given numbers.

 Let us understand the above steps using an example.

Example

Find the L C M of 40, 36 and 126 using the prime factorisation method.

Solution

We have been given the numbers 40, 36 and 126 and we are required to find the L C M of these numbers. Going by the above steps let us first find the prime factors of each of the given numbers. We have,

Prime factors of 40 are – 

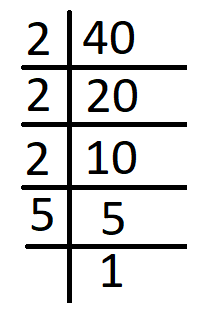
40 = 2 x 2 x 2 x 5

Prime factors of 36 are – 

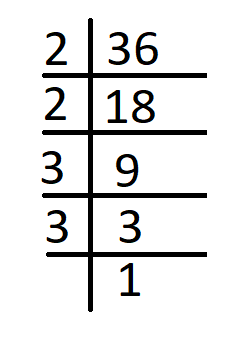
36 = 2 x 2 x 3 x 3

Prime factors of 126 are – 

126 = 2 x 3 x 3 x 7

We can see in the above prime factorisations of the above numbers, the number 2 appears a maximum of three times, which is the case in the number 40. Similarly, the number 3 appears as a factor for the maximum number of 2 times, which is the case in 36 and 126. The prime factors 5 and 7 occur only in 40 and 126 respectively. Therefore, the required L C M of the numbers, 40, 36 and 126 will be 

L C M of 40, 36 and 126 = 2 x 2 x 2 x 3 x 3 x 5 x 7 = 2520

Hence, L C M of 40, 36 and 126 = 2520

Let us take another example.

Example Sam has a camera that allows 24 exposures whereas Peter has a camera that allows 36 exposures. Both of them want to be able to take the same number of photographs and complete their rolls of the film. How many rolls should each buy?

Solution We have been given that Sam has a camera that allows 24 exposures whereas Peter has a camera that allows 36 exposures. Both of them want to be able to take the same number of photographs and complete their rolls of the film.

Since the film in Sam’s camera can take 24 exposures and the film in Peter’s camera can take 36 exposures and both of them want to take the same number of photographs while completing the rolls of the film as well, therefore, the total number of exposures taken by each will be the L C M of 36 and 24. Hence, let us find the L C M of 36 and 24.

We have,

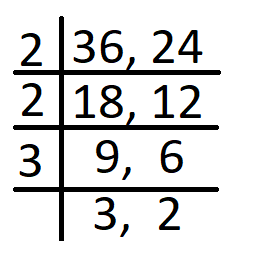
From above, we can see that the L C M of 36 and 24  = 2 x 2 x 3 x 3 x 2 = 72

  Hence, the number of rolls Sam should buy will be $\frac{72}{24}$  = 3

Similarly, the number of rolls Peter should buy will be $\frac{72}{36}$  = 2

Key Facts and Summary

  1. A multiple of a whole number is the product of the number and any counting number.
  2. A factor of a number is an exact divisor of that number. In other words, a factor of a number is that number that completely divides the number without leaving a remainder.
  3. 1 is a factor of every number. For example, 1 x 1 = 1, 4 x 1 = 4, 7 x 1 = 7 and so on
  4. Every number is a factor of itself. For example, we can write 6 as 6 x 1 = 6 which means that both 6 and 1 are the factor of the number 6. Similarly, we can write 12 as 12 x 1 = 12 which means that both 12 and 1 are the factor of the number 12.
  5. Every factor of a number is an exact divisor of the number itself. For example, the factors of the number 12 are 1, 2, 3, 4, 6 and 12. We can see that each of these factors divides 12. We can check the same for other numbers as well.
  6. Every factor of a number is less than or equal to that number. For example, if we consider the factors of 18, we will have, 1, 2, 3, 6, 9 and 18. Out of these numbers, 18 itself is the largest factor and all other factors are less than 18.
  7. Factors of a given number are finite. We have seen in the previous property that the factors are 18 are 1, 2, 3, 6, 9 and 18 and there cannot be a factor that is greater than the number 18 itself. Since the number is finite, therefore, it will have finite numbers of factors only.
  8. The highest common factor ( H. C. F. ) of two or more numbers is the greatest or the largest among common factors.

Understanding Factors and Multiples 4th Grade Math Worksheets
GCF: Greatest Common Factor (Valentine’s Day Themed) Math Worksheets
LCM: Least Common Multiple (Earth Day Themed) Math Worksheets

Browse All Worksheets

Link/Reference Us

We spend a lot of time researching and compiling the information on this site. If you find this useful in your research, please use the tool below to properly link to or reference Helping with Math as the source. We appreciate your support!

  • "Prime Factorization". Helping with Math. Accessed on July 17, 2025. https://helpingwithmath.com/prime-factorization/.

  • "Prime Factorization". Helping with Math, https://helpingwithmath.com/prime-factorization/. Accessed 17 July, 2025.

  • Prime Factorization. Helping with Math. Retrieved from https://helpingwithmath.com/prime-factorization/.