Squares and Square Roots

Numerous mathematical and scientific applications exist for squares and square roots.

Some of the most fundamental categories of algebraic polynomials are built on the square function. The square function in trigonometry can be used to calculate the equivalent angles and side lengths of congruent triangles, making it a valuable tool for simulating periodic processes.

Square roots are used in physics to calculate a pendulum’s period. Additionally, statistics and finance both use the square root function.

The Pythagorean Theorem solves the distance between two points using the square and square root functions. 

Squares are the opposite of square roots in concept. As illustrated below, squaring seven is 42, but when we get the square root of 49, the result is 7.

What is the Square of a Number?

When a value is multiplied by itself, squares are the resulting numbers. Thus, a square is a product of multiplying a number by itself. For instance, a number 5 multiplied by itself produces a result of 25. In this situation, 25 is referred to as a perfect square.

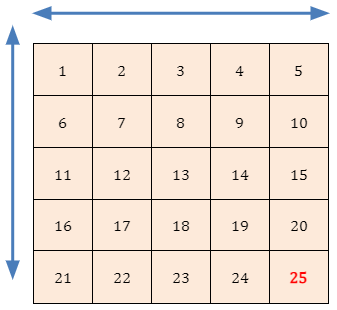
The arithmetic operator ( ² ) represents multiplying a quantity by itself. A number raised to the power of 2 is the same as squaring that number.

Because the resulting number, n², corresponds to the area of a square with sides of length n, raising a number n to the power of 2 is known as “squaring.”

What is a Perfect Square?

A number is considered a perfect square if it is a product of two equal numbers that are multiplied by one another. 

The table below shows the squares of numbers from 1 to 50.

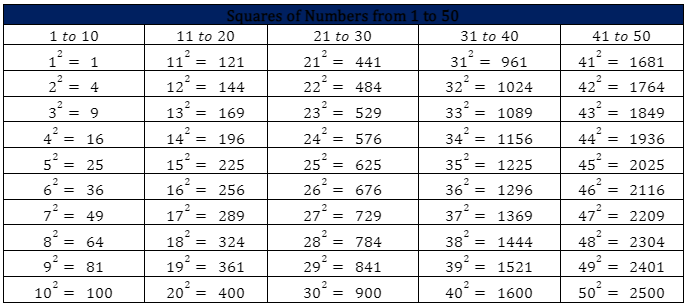
The products in this table are all perfect squares.

Properties of Square Numbers

Square numbers have the following properties.

1. Never should a number with a 2, 3, 7, or 8 at the unit’s position be a perfect square. Thus, none of the square numbers can end in 2, 3, 7 or 8. Additionally, the final digits of some square numbers could be 0, 1, 4, 5, 6, or 9.

Examples: 

These numbers end in either 2, 3, 7, or 8 and are not perfect squares.

12, 33, 47, and 98

These numbers have the final digits of either 0, 1, 4, 5, 6, or 9 and are perfect squares.

100, 81, 25, 36, and 49

2. Even numbers always result from squared even numbers. In addition, squared odd numbers always result in odd numbers. In simple terms, squares of even numbers are even, while the squares of odd numbers are odd.

Examples:

36.  is an even number, and it is a square of 6, which is also an even number.
37. is an odd number, and it is a square of 7, an odd number.

3. Numbers, with the unit place either 1 or 9, have squares end in 1.

Examples:

The square of 11, a number with a unit place of 1, is 121.
The square of 29, a number with a unit place of 9, is 841.
Both 121 and 841 ends in 1.

4. When a perfect square number is divided by 4, the remainder is either 0 or 1.

Example:

When 64 is divided by 4, the remainder is 0.
When 24 is divided by 4, the remainder is 1.

5. A number with an odd number of zeros at the end is never a perfect square. A number that ends with an even number of zeros, the number can be a perfect square.

Examples:

400, 900, 1600, 2500, and 3600 are numbers that end with an even number of zeros and are perfect squares.
10, 30, 1000, and 2000 are numbers that end with an odd number of zeros and are not perfect squares. 

6. A number’s square will always have a 6 at the end of the number ends in 4 or 6.

Examples:

196 and 256 are the squares of 14 and 16, respectively. These numbers end in 4 or 6, and their squares end in 6.
The square of 34 and 36 are 1156 and 1296, respectively. These numbers end in either 4 or 6, and their squares end in 6.

7. If n is the number of odd numbers, then the sum of consecutive n odd numbers is n².

The table below shows this property.

Consecutive odd numbers	Sum of Consecutive Odd Numbers	n Number of Odd Numbers	n2
1	1	1	12=1
1+3	4	2	22=4
1+3+5	9	3	32=9
1+3+5+7	16	4	42=16
1+3+5+7+9	25	5	52=25
1+3+5+7+9+11	36	6	62=36
1+3+5+7+9+11+13	49	7	72=49

Squares of Negative Numbers

A positive number will be the product of multiplying two negative numbers. The squares of negative numbers can be computed using this concept.

Examples:

( -4 ) x ( -4 ) =16

( -7 ) x ( -7 ) =49

( -9 ) x ( -9 ) =81

( -10 ) x ( -10 ) =100

( -12 ) x ( -12 ) =144

( -15 ) x ( -15 ) =225 

What is the Square Root of a Number?

A number’s square root is a value that, when multiplied by itself, gives the original number. The opposite of squaring an integer is finding its square root. Hence, a number’s square value is obtained by multiplying it by itself, whereas the square root of a number can be obtained by looking for a number that, when squared, gives the original value.

To denote square root, the symbol “√ ” is used. The number below the square root symbol is referred to as the radicand, whereas the square root symbol itself is known as a radical.

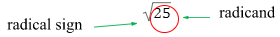
The table below shows the square roots of perfect squares from 1 – 2500.

Methods in Finding the Square Root of a Number

There are several ways to find the square root of a number, like prime factorization, repeated subtraction, long division, and estimation. To start the process, it is also essential to identify if the given number is a perfect square or not since it really helps on what method to use that will quickly solve the square root of that number. 

Square Root by Prime Factorization

These are the steps in finding the square root of a number by prime factorization:

Step 1: Identify the prime factors of the given number.
Step 2: Make factor pairs such that each pair’s two factors are equal.
Step 3: Select one number from each pair. And,
Step 4: Solve the product of the factors selected.

Example 1:

Find the square root of 324.

Solution:

Let us follow the steps to get a number’s square by prime factorization.

Step 1: Identify the prime factors of the given number.

Let us use factor trees to divide the number into its prime factors.

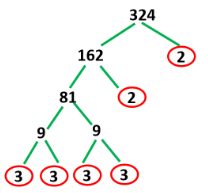
                     324=2 ×2 ×3 ×3 ×3 ×3

Step 2: Make factor pairs such that each pair’s two factors are equal.

The pairings of the prime factors of 324 are (2 ×2) x (3×3) x (3×3).

Step 3: Select one number from each pair.

Selecting from each pair, we have 2×3×3.

Step 4: Solve the product of the factors selected.

The product of 2×3×3 is 18. 

Therefore, the square root of 324 is 18.

Example 2:

Find the square root of 2025.

Solution:

Following the steps using prime factorization, we have,

Step 1: Identify the prime factors of the given number.

Using factor trees, let us find the prime factors of 2025.

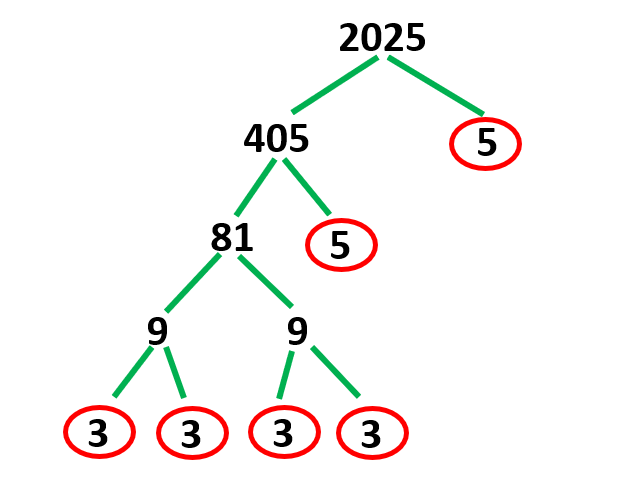
                     2025=3 ×3 ×3 ×3 ×5 ×5

Step 2: Make factor pairs such that each pair’s two factors are equal.

The pairings of the prime factors of 2025 are (3 ×3) x (3×3) x (5×5).

Step 3: Select one number from each pair.

Selecting from each pair we have, 3×3×5.

Step 4: Solve the product of the factors selected.

The product of 3×3×5 is 45. 

Therefore, the square root of 2025 is 45.

Square Root by Repeated Subtraction

The word “repeated” simply means that the process of subtraction is done several times. This method involves subtracting consecutive odd numbers from the number whose square root we are computing until we reach zero. The number of times we subtract is equal to the square root of the number we are solving. Only perfect square numbers can be calculated using this method. 

Example 1:

Find the square root of 36 using repeated subtraction.

Solution:

36-1=35
35-3=32
32-5=27
27-7=20
20-9=11
11-11=0

Notice that we have subtracted 1, 3, 5, 7, 9, and 11 for a total of 6 integers.

Hence, the square root of 36 is 6.

Example 2:

Using the method of repeated subtraction, find the square root of 144.

Solution:

144-1= 143
143-3= 140
140-5= 135
135-7= 128
128-9= 119
119-11= 108
108-13= 95
95-15= 80
80-17= 63
63-19= 44
44-21= 23
23-23= 0

Since we have subtracted 1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, and 23, for a total of 12 odd numbers, then the square root of 144 is 12.

Square Root by Long Division

If the numbers we need to get the square root are too big, this method may be applicable since prime factorization is most useful for small numbers. 

Finding the square root of 7225 using long division. we have,

Step 1: Draw lines at the top and to the left 7225.

Step 2: Mark pairs of the digits of 7225 starting from the unit’s end (right-most side end). In this example, 72 and 25 are pairs of numbers.

 Step 3: Find a perfect square number less than or equal to 72. Since 72 is not a perfect square, we will choose a perfect square number closest to 72.

7²=49
8²=64
9²=81
10²=100

Step 4: Since 8²=64, which is closest to 72, we will get these factors, 8×8, and write it to the left and above the lines as shown below.

Step 5: Multiply 8 by itself and write the product below 72. Also, add 8 with 8, write the sum (16) underneath, and subtract 64 from 72, which is 8.

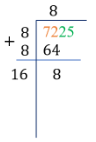
Step 6: Bring down the next pair and find a number that when we multiply ( 16 ? × ?), the product is less than or equal to 825.

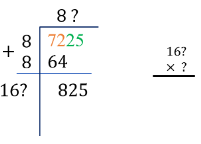
This missing value is five (5) since 165×5=825.

Step 7: Subtract the product of 165×5 from 825. Since the difference is zero, then 86²=7225.

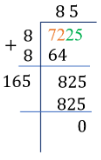
Square Root by Estimation Method

We can estimate the square root of a number by going through this tedious process. Some calculations are done easier by using estimates and approximations, which are justifiable guesses about the actual number. By the estimation method, let us find the square root of 10.

The first step is to identify the perfect square numbers nearest 10. Let us list down some numbers and their squares.

1²= 1
2²= 4
3²= 9
4²= 16

Since 3²=9 and 4²=16, this means that √10 lies between 3 and 4. 

Next, identify if √10 is closer to 3 or 4. To check if the value is closer to 3, we may try 3 to 3.5. To check if the value is closer to 4, we may try 3.5 to 4. Thus,

3²= 9(3.5)² = 12.254²= 16

 Since 10 is between 9 and 12.25, then √10 is between 3 and 3.5. 

Now, let us try some intervals between 3 and 3.5. For example, 3, 3.25 and 3.5,

3²= 9
(3.25)²= 10.5625
(3.5)²= 12.25

We can see that since 10 is between 9 and 10.5625, then 10 is between 3 and 3.25.

If we continue the same process of estimation, we may have,

(3.1)²= 9.61
(3.2)²= 10.24

This means that √10 is closer to 3.1. 

If we want to get the value up to 2 decimal places, we may have,

(3.10)²= 9.61
(3.12)²≈ 9.73
(3.14)²≈ 9.86
(3.16)²≈ 9.99
(3.18)²≈ 10.11

Therefore, √10 is approximately 3.16.

Estimation is a long process and is most applicable if the given number is not a perfect square (imperfect square).

Square Root of Negative Numbers

Since multiplying two negative numbers always result in a positive number and zero is a square root of itself, how do we then get the square root of negative numbers?

Among the set of Real Numbers, all negative numbers do not have a square root. But, the square root of a negative number can be solved using complex numbers. Let us say, for instance, we want to find the square root of (- 81).

Using the factors of -81, $\sqrt{-81}$ can be written as,

$\sqrt{-81}= \sqrt{81 × (-1)} = \sqrt{81} × \sqrt{-1}$

In this solution, 81 is equal to 9. Since there is no real root of -1 and it does not exist in real numbers, it is called an imaginary number. The imaginary number -1 is denoted by the letter i.

Thus, $\sqrt{-81}=\sqrt{81} x \sqrt{(-1)} =9i$

Examples:

1. $\sqrt{-100} = \sqrt{100 × ( -1 )} = \sqrt{100} × \sqrt{-1}= 10i$
2. $\sqrt{-25} = \sqrt{25 × ( -1 )} = \sqrt{25} × \sqrt{-1}= 5i$
3. $\sqrt{-169} = \sqrt{169 × ( -1 )} = \sqrt{169} × \sqrt{-1}= 13i$
4. $\sqrt{-256} = \sqrt{256 × ( -1 )} = \sqrt{256} × \sqrt{-1}= 16i$
5. $\sqrt{-1089} = \sqrt{1089 × ( -1 )} = \sqrt{1089} × \sqrt{-1}= 33i$

Word Problems 

Example 1:

A square coffee table has an area of 2500 cm². Calculate the length of the side of the coffee table.

Solution:

Since the given area of a square coffee table is 2500 cm², then we just need to get its square root to find the length of each side. So we have,

√2500 = 50

In conclusion, each side of the square coffee table is 50 cm long.

Example 2:

Ashley wants to cover the floor of her square room with carpet. If the length of each side is 7 feet, find the area of the floor carpet she needs.

Solution:

Finding the area of a square given its length, we need to get the square of the side’s length or multiply the side’s length by itself.

7² = 49

Hence, the area of the floor carpet must be 49 ft².

Example 3:

A gardener divided a lot into 6 square sections. If the length of the side of each square section is 5 meters, find the total area of the lot.

Solution:

Let us first get the area of each square section. Since the length of the side of each square section is 5 meters, then each area is 25 m².

5²= 25

To get the total area of the lot, 25 must be multiplied by 6, giving us 25 × 6 =150.

Hence, the total area of the lot is 150 m².

Example 4:

The image below shows the layout of the 3 square lots of Mrs. Lopez. Find the length of the side of each square lot given this information:

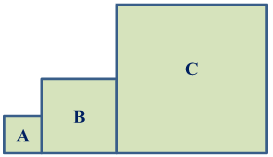
Area of Lot A = 4 ft²

Area of Lot B = 16 ft²

Area of Lot C = 64 ft²

Solution:

Finding the length of the side of each square lot, we must get the square roots of the given areas. 

√4=2
√16=4
√64=8

Thus, the length of the side of square Lot A is 2 ft., the length of the side of square Lot B is 4 ft., while the length of the side of square Lot C is 8 ft.

Example 5:

A particular square has a perimeter of 60 cm². Find the length of the side of the square and its area.

Solution:

Since we know the perimeter of the square, which is 60 cm²., and the perimeter of a square is the total of all the lengths of its side, then we can solve its length by dividing 60 by 4. The divisor is four because the number of sides of a square is 15. 

Now, to calculate the area of the square, we have 15² = 225.

Therefore, the length of the side of the square is 15 cm. and its area is 225 cm².

Summary

• When a value is multiplied by itself, squares are the resulting numbers. Thus, a square is a product of multiplying a number by itself.
• A number is considered a perfect square if it is a product of two equal numbers that are multiplied by one another. 
  Examples of perfect square numbers are 25, 36, 49, 81, 121, 169, etc.
• The arithmetic operator ( ² ) represents multiplying a quantity by itself.   A number raised to 2 is the same as squaring that number.
• The square of a negative number is positive.
  (-10)²=-10×-10=100
• A number’s square root is a value that, when multiplied by itself, gives the original number.  
• To denote square root, the symbol “√ ” is used. The number below the square root symbol is referred to as the radicand, whereas the square root symbol itself is known as a radical.
• The opposite of squaring an integer is finding its square root.
• These are the methods to find the square root of a number:
  Prime Factorization
  Repeated Subtraction
  Long Division, and 
  Estimation.
• Among the set of Real Numbers, all negative numbers do not have a square root. However, the square root of a negative number can be solved using complex numbers.
• The imaginary number $\sqrt{-1}$ is denoted by the letter i.

Recommended Worksheets

Square Root (Labor Day Themed) Math Worksheets
Measuring Area Using Square Grids (Painting Themed) Worksheets
Square Numbers (International Museum Day Themed) Math Worksheets