Exponential Function | Definition, Examples, Formula, Domain

Introduction

Functions forms one of the most important building blocks of Mathematics. The word “ Function“ has been derived from a Latin word meaning operation and the words mapping and map are synonymous to it. There are many standard defined functions that we use such as modulus functions, logarithmic functions etc. one of such standard functions is the exponential function. Let us learn more about this function. But, before that let us recall some basic concepts pertaining to functions that are integral to the understanding of exponential functions.

Function as a Special Kind of Relation

Let A and B be two non-empty sets. A relation f from A to B, i.e. a subset of A x B is called a function or a mapping or a map from A to B is,

For each a ∈ A there exists b ∈ B such that ( a, b ) ∈ f
( a, b ) ∈ f and ( a, c ) ∈ f ⇒ b = c

Thus a non-void set f of A x B is a function from A to B if each element of A appears in some ordered pair in f and no two ordered pairs in f have the same first element.

If ( a, b ) ∈ f, then b is called the image of a under f.

Domain, Co-domain and Range of a Function

Let f : A → B. then the set A is known as the domain of f and the set B is known as the range co-domain of f. The set of all f-images of elements of A is known as the range of f or image set of A under f and is denoted by f ( A ).

Thus f ( A ) = { f (x) : x ∈ A } = Range of f

Real Functions

Some functions have domain and co-domain both as subsets of the set R of all real numbers. Such functions are called real functions or real valued functions of the real variable. In other words, a function f : A → B is called a real valued function, if B is a subset of R, where R is the set of all real numbers.

Onto Functions

A function A → B is said to be onto function or a surjection if every element of B is the f-image of some element of A, i.e. f ( A) = B or range of f is the c-domain of f.

Thus f : A → B is an onto function iff for each b ∈ B there exists a ∈ A such that f ( a ) = b

One-One Functions

A function A → B is said to be a one-one function or an injection if different elements of A have different images of B.

Thus f : A → B is one-one

⇔ a ≠ b ⇒ f ( a ) ≠ f ( b ) for all a, b ∈ A

⇔ f ( a ) = f ( b ) ⇒ a = b for all a, b ∈ A

Many-One Functions

A function A → B is said to be a many-one function if two or more elements of set A have the same image in B.

Thus f : A → B is many-one if there exists x, y ∈ A such that x≠ y but f ( x ) = f ( y )

Let us now learn about exponential function.

What is exponential function?

If a is a positive real number other than unity, then a function that associates each x ∈ R to a^x is called the exponential function. In other words, an exponential function is a Mathematical function in form f (x) = a^x, where “x” is a variable and “a” is a constant which is called the base of the function and it should be greater than 0.

Formula for Exponential Function

A function f : R → R defined by f ( x ) = a^x , where a > 0 and a ≠ 1 is the formula for the exponential function. Hence, we have

f ( x ) = a^x

where

a > 0 and a ≠ 1 and x is a real number

It is important to note here that is we have negative values for the variable, the exponential function is not defined when – 1 < x < 1.

The curve of the exponential graph is dependent upon the exponential function which further is dependent upon the value of x. Therefore, it is the value of x that defines the curve of the graph of exponential function.

What is the domain and the range of an exponential function? Let us find out.

Domain of an exponential function

We know that the domain of a function y = f ( x ) is the set of all x-values where it can be computed and the range is the set of all y-values of the function. The domain of an exponential function is R the set of all real numbers.

Range of an exponential function

The range of an exponential function is the set ( 0 , ∞) as it attains only positive values.

There are two terms are related to exponential function and are used in day to day real life situations as well. These terms are exponential growth and exponential decay. Let us learn more about them.

Exponential Growth

If the quantity initially increases at a very slow rate and rapidly increases at later stages, it is termed as exponential growth. Over time an increase in the rate of change is noticed which on the passage of time, becomes faster. Such an increase is termed as an exponential increase. So, how do we define an exponential growth using a formula? The formula for an exponential growth is given by –

y = a ( 1 + r ) ^x

where, r is the percentage of growth.

Exponential Decay

Exponential decay, on the other hand is said to have occurred when a quantity initially decreases very rapidly and then slowly sees and increasing trend. Over time a decrease in the rate of change is noticed which on passage of time, becomes faster. Such a decrease is termed as an exponential decrease or exponential decay. So, how do we define an exponential decrease using a formula? The formula for an exponential decrease is given by –

y = a ( 1 – r ) ^x

where, r is the percentage of decay.

Let us now learn about the graph of an exponential function.

Graph of an Exponential Function

We shall consider different cases while discussing the graph of an exponential function.

Case 1 : When a > 1

Let us observe the values of y = f ( x ) = a ^x as the value of x increases.

Also, we know that

f ( x ) = {<1 for x<0 =1 for x=0 >1 for x>0

Therefore, the graph of an exponential function f ( x ) = b ^x for b > 1 will be given by –

For example, let us consider the graph of y = 2 ^x.

The graph of this function will be

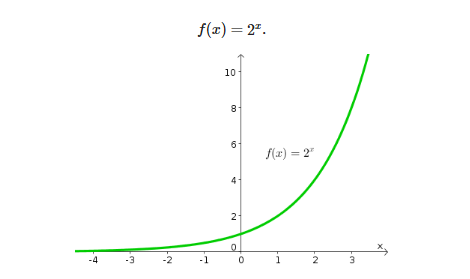
We can see that the above exponential function increases rapidly.

Also, we can clearly observe that –

2 ^x < 3 ^x < 4 ^x < …… for all x > 1
2 ^x = 3 ^x = 4 ^x < …… = 1 for all x = 0
2 ^x > 3 ^x > 4 ^x > …… for all x < 1

Hence, the graphs of f ( x ) = 2 ^x , f ( x ) = 3 ^x , f ( x ) = 4 ^x in accordance with the graph shown above.

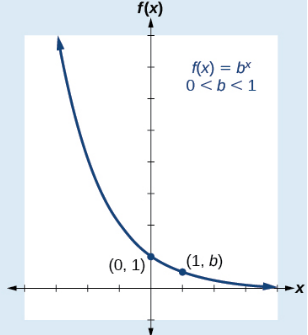
Case 2 : When 0 < a < 1

In this case, the values of y = f ( x ) = a ^x decrease with the increase in x and y > 0 for all x ∈ R. Also, we know that –

f ( x ) = {<1 for x<0 =1 for x=0 >1 for x>0

Thus, the graph of f ( x ) = b ^x for 0 < b < 1 as shown below –

Let us now learn about properties of exponential functions –

Properties of Exponential functions

Following are the general properties of exponential functions –

The domain of all exponential functions is the set of real numbers.
The range of exponential functions is y > 0.
The graph of exponential functions may be strictly increasing or strictly decreasing graphs.
The graph of an exponential function is asymptotic to the x-axis as x approaches negative infinity or it approaches positive infinity.
The graph of an exponential function increases without bound as x approaches negative infinity or it approaches positive infinity.
An exponential graph is always continuous.
An exponential graph is a smooth graph.

Let us discuss the above properties using an example.

Let us take the example of the graph of the function f ( x ) = 2 ^x .

We have seen above that the graph of this function is given by –

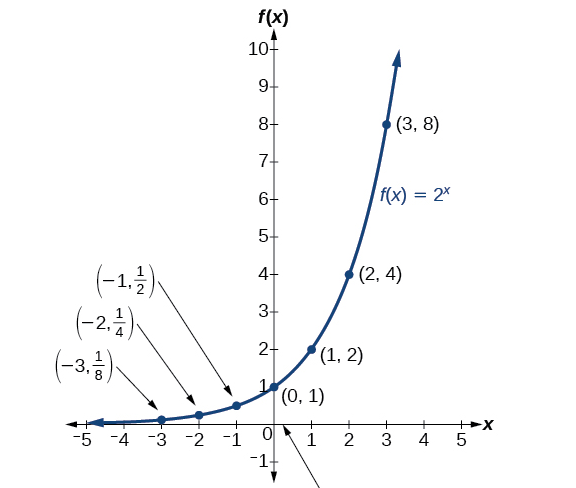
What are the properties of this graph? The properties of this graph are –

The domain of the function f ( x ) = 2 ^x is the set of real numbers.
The range of the function f ( x ) = 2 ^x is y > 0.
The graph of the function f ( x ) = 2 ^x is a strictly increasing graph.
The graph of the function f ( x ) = 2 ^x is asymptotic to the x-axis as x approaches negative infinity.
The graph of the function f ( x ) = 2 ^x increases without bound as x approaches positive infinity.
An exponential graph of the function f ( x ) = 2 ^x is always continuous.
An exponential graph of the function f ( x ) = 2 ^x is a smooth graph.

Let us consider another example. What would be the graph of the function f ( x ) = 2 ^{– x}

The graph of the function will be –

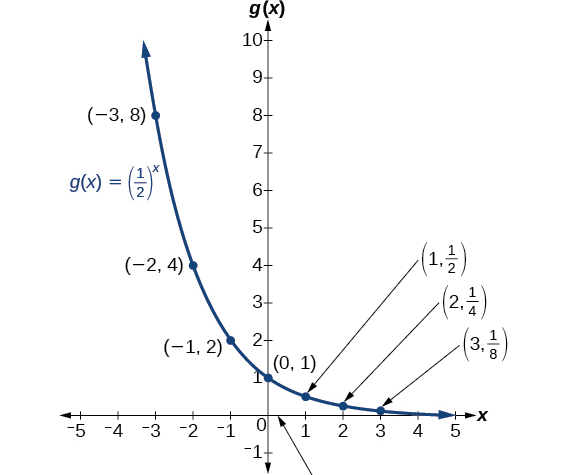
What are the properties of this graph? The properties of this graph are –

The domain of the function f ( x ) = 2 ^{– x} is the set of real numbers.
The range of the function f ( x ) = 2 ^{– x} is y > 0.
The graph of the function f ( x ) = 2 ^{– x} is strictly decreasing graph.
The graph of the function f ( x ) = 2 ^{– x} is asymptotic to the x-axis as x approaches positive infinity.
The graph of the function f ( x ) = 2 ^{– x} increases without bound as x approaches negative infinity.
An exponential graph of the function f ( x ) = 2 ^{– x} is always continuous.
An exponential graph of the function f ( x ) = 2 ^{– x} is a smooth graph.

Rules of Exponential functions

The rules of exponential function are as same as that of rules of exponents. Some of these rules are –

Law of Zero Exponent This law states that , if we have an exponential function, a ^x where, x = , then a ⁰ = 1
Law of Products – According to this law, if we have two exponential functions, namely a ^m and a ⁿ, then the product of these two functions will be given by a ^m x a ⁿ = a ^{m + n}
Law of Quotients – According to this law, if we have two exponential functions, namely a ^m and a ⁿ, then the division of these two functions will be given by a ^m ÷ a ⁿ = a ^{m – n}
Law of power of power – According to this law, if we an exponential function, namely a ^m and this function is further raised to the power of n, we will have (a ^m ) ⁿ = ( a ) ^{m n}
Law of Power of a Quotient – According to this law, if we an exponential function, namely ( $\frac{a}{b}$ ) ^m then this function can also be written as $\frac{a^m}{b^m}$.
Law of Negative Exponents – According to this law, if we an exponential function, namely a ^– ^m, then this function can also be written as $\frac{1}{a^m}$.

Key Facts and Summary

Let A and B be two non-empty sets. A relation f from A to B, i.e. a subset of A x B is called a function or a mapping or a map from A to B is,
1. For each a ∈ A there exists b B such that ( a, b ) ∈ f
2. ( a, b ) ∈ f and ( a, c ) ∈ f ⇒ b = c
Let f : A → B. then the set A is known as the domain of f and the set B is known as the range co-domain of f. The set of all f-images of elements of A is known as the range of f or image set of A under f and is denoted by f ( A ).
If a is a positive real number other than unity, then a function that associates each x ∈ R to a ^x is called the exponential function.
A function f : R → R defined by f ( x ) = a ^x , where a > 0 and a ≠ 1 is the formula for the exponential function.
The domain of an exponential function is R the set of all real numbers.
The range of an exponential function is the set ( 0 , ∞) as it attains only positive values.
If the quantity initially increases at a very slow rate and rapidly increases at later stages, it is termed as exponential growth. The formula for an exponential growth is given by y = a ( 1 + r ) ^x , where, r is the percentage of growth.
Exponential decay, is said to have occurred when a quantity initially decreases very rapidly and then slowly sees and increasing trend. ? The formula for an exponential decrease is given by y = a ( 1 – r ) ^x , where, r is the percentage of decay.
The domain of all exponential functions is the set of real numbers.
The range of exponential functions is y > 0.
The graph of exponential functions may be strictly increasing or strictly decreasing graphs.
The graph of an exponential function is asymptotic to the x-axis as x approaches negative infinity or it approaches positive infinity.
The graph of an exponential function increases without bound as x approaches negative infinity or it approaches positive infinity.
An exponential graph is always continuous.
An exponential graph is a smooth graph.
The rules of exponential function are as same as that of rules of exponents.

Recommended Worksheets

Exponents (Museum Themed) Worksheets
Understanding Exponents 6th Grade Math Worksheets
Multiplication of Functions (Travel and Tours Themed) Worksheets

Browse All Worksheets

We spend a lot of time researching and compiling the information on this site. If you find this useful in your research, please use the tool below to properly link to or reference Helping with Math as the source. We appreciate your support!