Introduction:
Fractions are sometimes misunderstood as being difficult to understand, although they’re actually quite simple. When we don’t understand the fundamentals of a mathematical idea, we can wind up biting our nails for the rest of our lives. This should not be the case with fractions, since we will examine them as well as the fundamentals of fractions in this post, making them totally accessible to all.
Definition
Fractions are fractional numbers that indicate a portion of a whole. Every solitary part of an object or a group of objects is a fraction when they are divided into equal parts. In most cases, a fraction is represented as 1/2, 5/12, 7/18, and so forth.
A fraction is a piece of an object that is a part of the whole. It has this shape.
a/b.
The term “fraction” comes from the Latin word “fractious,” which meaning “broken.”
Fraction has existed since the Egyptian era, which is considered to be one of the world’s earliest civilizations. Fractions, on the other hand, were not considered numbers; instead, they were used to compare whole numbers to each other.
The numerator is the top part, while the denominator is the lower part.
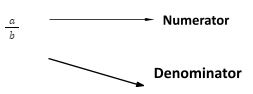
The numerator denotes the total number of equal parts into which whole is divided, whereas the denominator represents the total number of equal parts into which the complete is divided. The number of equal pieces removed is the numerator.
Example
The numerator and denominator of the fraction 3/4, for example, are 3 and 4.
Hence, Fractions are indeed the mathematical representation of something that is split into two or more components. The denominator and numerator are the two elements of a fraction. A slash separates them in the printed expression.
The term fraction is often used in mathematics to indicate algebraic equation that isn’t rational values (where the numerator and denominator are not integers).
As example, formulas containing radicals, such as rad2/2, and fractions, such as pi/4, are both called fractions.
There are additional mathematical fractions with unknown values for a and b (assuming b = 0), including such ab.
Example
We want to divide sheet into three equal parts
Let’s break something down into its constituent elements. Let’s just cut an apple into four pieces. We wish to give away three parts of the apple after we’ve divided it, leaving us with only one.
Because we want to create a percentage out of the divide we simply did, we’ll give 3/4th of an orange.
Examples
- $\frac{1}{5}$
- $\frac{45}{7}$
- 5/6
- 99/100
- ½
A Fraction in the Real World
Ones birthday is approaching, and your mother has placed an order for pizza for both you and your pals. When individuals open the pizza box, one’ll notice that it’s already been cut into slices. Assume there are eight slices and you have seven buddies. As such, there are eight people eating the eight segments of pizza.
Types of fraction
Fractions are divided into three categories in mathematics.
Proper fractions, improper fractions, and mixed fractions are the three types. Fractions are terms with a denominator and a numerator. We describe its types based on these two terms.
The terminology used to identify the pieces of a whole item is fractions. Bread, for instance, is cut into four pieces, with each piece representing a quarter of the bread. The numerator is 1 and the denominator is 4.
The denominator displays how many portions the apple is divided into, while the numerator reveals how many pieces we have given out. The denominator would have been 6 instead of 4 if we had divided the apple into 6 parts. And a half of an apple will be 1/2.
To express a fraction on a number line, do the following:
1. Make a number line in the middle of the page.
2. Cover the 0 and 1 location (leave enough of space)
3. Between 0 and 1, the denominator (bottom) will inform you how many equal parts you need to make.
4. To depict the fraction, the numerator (top) will inform you how many equal parts to color.
Types of fraction
There really are two simple choices in a fraction:
The denominator is greater than the numerator.
The numerator exceeds the denominator.
Fractions that are proper
Definition
It’s a Proper Fraction when the numerator is less than the denominator. These fractions are all smaller than one, and none of them will be on the number line beyond one. The numerator is the number of equal parts that the whole is divided into.
Example
The numerator is the number of these equal components that are taken into account. The pizza example above, for each person receiving 1/8th of the pizza, is an instance of a correct fraction.
Improper Fraction
Definition
It’s an Improper Fraction when the numerator is greater than the denominator. Those fractions are greater than one and lie on the number line beyond one. When more than one thing is divided evenly into particular sections, the comes into play. The number of equal parts necessary is represented by the denominator. The numerator is the total number of items.
Examples
A proper fraction is 3/4, while an incorrect fraction is 8/5.
An erroneous fraction necessitates the use of elements from a different piece with same object. 6/4th of an apple, for example, indicates that the remaining two apple slices were taken from some other apple.
Arithmetic with fractions
Fraction addition and subtraction
Denominators in common
When the numbers on the bottom are the same, adding and subtracting fractions is simple.
The denominators are the numbers that make up a fraction.
Examples
$\frac{5}{9}+\frac{3}{9} = \frac{8}{9}$
$\frac{5}{9} – \frac{3}{9} = \frac{2}{9}$
When subtracting fractions, the denominator of the fractions are same, we simply subtract the numerators once the fractions have the same denominator.
= denominator/numerator
What about if the denominators of the fractions are different? In this situation, we find the least common multiple of the denominators to make them equal (LCM).
Improper Fractions with Different Denominators Added and Subtracted
- Step 1: Between both the denominators, get the Lowest Common Multiple (LCM).
- Step 2: Multiply each fraction’s numerator and denominator by a number in this
- As just a new denominator, they’ve chosen the LCM.
- Step 3: Keeping the denominator the very same, add or remove the numerators.
- Step 4: Convert the fraction to a mixed number if the solution is in an inappropriate form.
Example
Subtract the fractions from the overall.
$\frac{1}{2} – \frac{1}{3}$
Step 1: Make a list of all the 2 and 3 digit multiples.
Multiples of 2 are 2, 4, 6, 8, 10, 12…
Multiples of 3 are 3, 6, 9, 12, 15, 18 …
Among 2 and 3, the Least Common Multiple is 6.
Step 2: a) Find a variety that, once multiplied by the underside of the scale, equals
as the new denominator, we get the LCM (6)
$\frac{1 x 3}{2 x 3} = \frac{3}{6}$
$\frac{1 x 2}{3 x 2} = \frac{2}{6}$
$\frac{3}{6} – \frac{2}{6}$
3: We can now subtract the numerators of our fractions because they now contain equal sized slices. As a result, we have
= $\frac{1}{6}$
Hence,
Crossing multiple of the first fractions’ numerator to the subsequent fraction’s denominator, as well as the second fraction’s numerator to first fraction’s denominator
So multiply the denominators together.
Division of fractions
Division, like whole numbers, entails forming equivalent groups. Students realize the link between equal and fair sharing as a result of their previous experiences with sharing and division.
A fraction is the result of dividing two integers by their quotient. As instance, if we want to split three objects evenly among five individuals, students understand that division may be used to solve the problem. However, because the quotient of 4/7 cannot be represented with a whole number, additional numbers must be presented: the fraction 4/7.
Fractions in Comparison
- Step 1: Evaluate the denominators of two fractions. Rewrite one or both fractions with a common denominator if they are distinct.
- Step 2: Double-check the denominators. The fraction with the larger numerator is the greater fraction if the denominators are the same. The fraction with smallest numerator is the smallest. And, as previously stated, the fractions are identical if the numerators are identical.
- The fraction with larger numerator is the greater fraction, because it comprises more parts of the whole, as long as the denominators are the same. Because it comprises fewer pieces of the whole, the fraction with the smaller numerator is the smaller fraction.
- Remember that the sign stands for “less than,” whereas the symbol > stands for “greater than.” Inequality symbols are represented by these symbols. As a result, the accurate statement 3 8 means “3 is less than 8,” while the false assertion 5 > 3 means “5 is bigger than 3.” Think about the smaller end of the symbol pointing to the smaller number to help you recall the difference between the two characters.
- This implies that to obtain equivalent fractions, both numerator (top number) and denominator (bottom number) must be multiplied by the very same number.
- As a result, the concept of equivalence is comparable to the idea of equality.
Ratios of Fractions
Fractions can also be defined as a ratio. 3 /11, for instance, can be interpreted as the chance of an occurrence occurring five times out of eight. Component, like the ratio of males to females in class, and part-whole, such as the ratio of males to the entire class, are two ways to represent ratios.
Students’ ability to gain a mental understanding of fractions is dependent on their ability to communicate in fractional language. However, this does not imply that educators should focus solely on teaching fraction definitions; rather, educators should begin by explaining what fractions are. Fractions are indeed a way of representing and describe a portion of a larger whole.
Rules for simplify fraction
Even before we follow the rules, simplifying fractions is an easy.
- When our solution isn’t in the format needed by the challenge, we’ll need to reduce fractions. In fact, most math teachers will insist that you always write the resultant fraction in its most basic form.
- In practice, there are two situations in which simplifying your response is important.
- Our answer could actually be a higher level equivalent proper fraction, which is better stated in its reduced state or lowest component. When feasible, many instructors will suggest that students shorten the response.
- In addition, numerous procedures will frequently result in an erroneous fraction. The numerator is greater than the denominator in this case. We’ll need to convert these answers to a mixed number in order to write them in their simplest form. The Whole Parts and Fractional Part will be represented in this way.
Fractions Reduced to Its Lowest Equivalent
This is how to simplify or reduce fractions to their simplest form…
$\frac{ac}{bc} = \frac{a x c}{b x c} = \frac{a}{b}$
Just remember…
Everything we have to a fraction’s numerator must also be done to the denominator. If the numerator must be divided by a number, the denominator must likewise be divided by the same number. You won’t modify the fraction’s total value this way.
To arrive at our reduced solution, we divided the numerator and denominator by “c” in our rule.
Here’s what’s going on. Although you have correctly calculated the fractions, your solution may well not showed lowest equivalent fraction. Breaking down both of the numerator and the denominator into prime integers is the quickest technique to ensure that your answer is in its simplest form.
Prime Factorization is the term for this procedure.
And here is an example to help us to determine…
$\frac{1}{6} + \frac{1}{6} = \frac{2}{6}$
= $\frac{2}{3 x 2} = \frac{2}{3}$
Observe that even after combining the fractions, the original answer is “2/4.” We must factor the numerator and denominator with prime numbers to see if our solution is in its simplest form.
The primes that are similar both to numerator and the denominator are just what we’re searching for. We then can balance out these frequent numbers if we discover them. The outcome is a fraction that has been reduced to its smallest comparable fraction.
The answer is not in its simplest form since “2” is a common element in both the numerator and denominator of our example above. As a result, we divided by “2” one for one to cancel out (/)one of the 2s in both the numerator and denominator. The final outcome is a “reduced fraction” that has been simplified to its simplest form.
Improper Fractions Simplified
One might recall that an improper fraction is one in which the numerator is bigger than the denominator. As a result, whenever you conduct a fractional operation and your result is an improper fraction, you will almost always have to reduce the answer. The outcomes will be expressed as a composite number.
To make a mixed number out of an incorrect fraction, simply divide the numerator even by denominator. There would be a whole number and a fractional part of the answer.
Example
= $\frac{13}{2}$
= $6 \frac{1}{2}$
As we can see, this is a relatively simple procedure. However, remember that when there is no leftover, the solution is the WHOLE NUMBER.
Make sure the remaining fraction is written in the simplest language possible. If not, you’ll have to lower it.
As we can see, simplifying fractions is not a difficult task. Simply follow the procedures above, and converting fractions to their simpler form will be a good thing.
Fraction Conversion:
A fraction is a fraction of a whole. The numerator and denominator are the two elements of a fraction. The term “conversion” refers to the process of changing a phrase from one form to another. Converting from fraction to decimal, fractions to percent, and improper fractions to mixed fractions and conversely are all examples of fraction conversion.
Decimal to Fraction Conversion
The following steps can be used to convert a decimal to a fraction:
We’ll use the decimal 0.25 as an example in this circumstance.
Rewrite a decimal number as just a fraction with one as the denominator and the decimal number as that of the numerator.
Both the numerator and denominator should be multiplied by 10 to the power of the series of numbers after the decimal point. If there is just one number after the decimal, multiply by ten; whether there are two, multiply by one hundred; whether there are three, increase by one thousand, and so on.
Example
17.48 = 1748/100
= 437/25 improper value
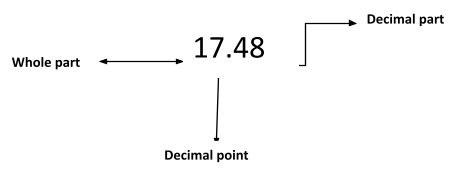
Fraction conversion is the process of changing a fraction from one form to the other, such as from fractions to digits or fractions to percents. It’s important to remember that you must divide the numerator by the denominator to convert a fraction to a decimal. Moreover, divide the numerator by the denominator to convert a fraction to a percentage. The decimal is then multiplied by 100.
Conclusion
- Fractions are a common occurrence in our daily lives.
- Fractions are used in a variety of situations, ranging from simple apple cutting to complex scientific studies.
- Fractions are quite helpful in simplifying arithmetic.
- Equivalent fractions concepts assist us in determining and calculating larger parts as well as reducing them to comparable smaller portions.
- Fractions can also be converted to decimals, which is useful in our financial system.
Recommended Worksheets
Proper and Improper Fractions (Winter Themed) Math Worksheets
Multiplication of Proper Fractions (Veterans Day Themed) Worksheets
Multiplication of Unlike Fractions (Thanksgiving Themed) Worksheets









