Decimals in a Number Line

Introduction

We have learnt different methods to represent a number such as a number written in words, a number written in numerals etc. we have also learnt about visual representation of numbers using a number line. Another fact which we are aware of is the different types of numbers such as natural numbers, whole numbers, fractions, decimal numbers, rational numbers etc. We have leant these concepts individually such as plotting a number on a number line, or adding or subtracting decimals. Now, let us learn some concepts that combine these individual identities such plotting a decimal number on a number line. But, before that we must recall some basic definitions and concepts that are integral to this learning. 

What are Decimals?

We know that a decimal indicates a part of a whole. In other words, decimals are another form of a fraction in which the whole number is separated from the fractional part using a dot.

What is a Number Line?

A number line is a straight horizontal line with numbers placed at even intervals that provides a visual representation of numbers. Primary operations such as addition, subtraction, multiplication, and division can all be performed on a number line. The numbers increase as we move towards the right side of a number line while they decrease as we move left.

Representation on a Number Line

Above is a visual representation of a standard number line. As is clearly visible, as we move from left to right, there is an increase in the value of numbers while it decreases when we move from right to left.

How are Decimal Numbers Represented on a Number Line?

Now, that we know what decimal numbers are and what is a number line, let us move to representing a decimal number on a number line. Representing decimal on a number line is defined as the plotting of decimal numbers on a number line.

An important aspect of decimals that needs to be understood for plotting them on a number line is that the decimals are place between two integers.

Let us understand this by an example.

Let us take two numbers 0 and 1 draw a number line between them. We will have,

Next, let us split the space between 0 and 1 into tenths. We will have the fractional values such as one-tenth, two-tenth, three-tenth and so on. It can be represented on the number line in the following manner.

Now, we know that 

One-tenth = 0.1

Two-tenth = 0.2

Three-tenth = 0.3 and so on.

Therefore, if we want to represent the above tenth values in the form of decimals we will have,

 Further, if we wish to plot a decimal number say, 0.6, we will mark it as

In the above example, we had a simple decimal number and it was quite easy to plot it. But we know according to the place value system of decimals we have decimal numbers such as one-tenth ($\frac{1}{10}$ ), one-hundredth ( $\frac{1}{100}$ ), one-thousandth ( $\frac{1}{1000}$ ) etc. so how will we plot these numbers? Let us find out.

Representing Tenths on a Number Line

We already know how to represent fractions on a number line. Let us now represent tenths of a decimal on a number line. But, let us recall what we means by tenths of a decimal?

Consider the following figure. It is divided into ten equal parts and one part is shaded. The shaded part represents one-tenth of the whole figure. It is written as $\frac{1}{10}$. $\frac{1}{10}$ is also written as 0.1 which is read as “ point one “ or “ decimal one “.

Thus the fraction $\frac{1}{10}$ is called one-tenth and is written as 0.1.

Now, let us represent tenths on a number line. We can understand this by an example.

Let us represent 0.4 on a number line. We can clearly see that there are 4 tenths in 0.4. Therefore in order to represent 0.4 on a number line we will divide the unit length between 0 and 1 into 10 equal parts and take 4 parts as shown below – 

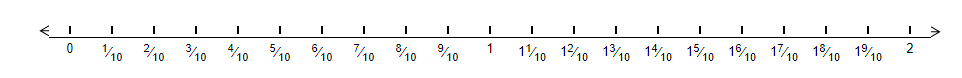
Now, we can know that 0.4 in fraction form is equal to 4/10. Hence we will mark 4/10 as 0.4 which is our desired mark on the number line. 

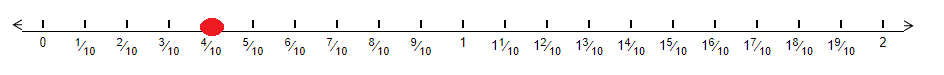
The steps that we used above to represent a tenth on a number line can be summarised as  –

1. We draw a number line between 0 and 1.
2. We then raw 10 lines dividing the total distance between 0 and 1 into 10 equal parts.
3. Now, one whole divided into 10 parts is equal to  $\frac{1}{10}$.
4. $\frac{1}{10}$ in decimal form is equal to 0.1.
5. At each new line we are adding $\frac{1}{10}$ or 0.1.
6. So, between 0 and 1 we have, 0 . 1 , 0 . 2 , . 0 . 3 , 0 . 4 , 0 . 5 , 0 . 6 , 0 . 7 , 0 . 8 and 0 . 9. Similarly, between 1 and 2 we have, 1 . 1 , 1 . 2 , 1 . 3 , 1 . 4 , 1 . 5 , 1 . 6 , 1 . 7 , 1 . 8 and 1 . 9.
7. We can also say that the line representing $\frac{1}{2}$ or 0.5 is the half way mark between 0 and 1. Similarly, the line representing $1\frac{5}{10}$ or 1.5 is the half way mark between 1 and 2.
8. Ten tenths is equal to one whole.

The above process can be defined as – “To represent a tenth on a number line, we will first have to divide the distance between two whole numbers into 10 equal parts to get their tenths values. Next we plot the tenths values that lie between the whole parts.”

Representing Hundredths on a Number Line

Let us now represent hundredths of a decimal on a number line. But, let us recall what we means by hundredths of a decimal?

If an object is divided into 100 equal parts, then each part is one hundredths of the whole. This means that –

One thousandth = $\frac{1}{100}$ which in decimal form is equal to 0.01

If we take 7 parts out of 100 equal parts of an object, then 7 parts make $\frac{7}{100}$ of the whole and it is written as 0.07.

Now, let us represent hundredths on a number line. We can understand this by an example.

Let us represent the thousandth value of the number 7.45 on a number line. 

To represent 7.4 on a number line, we first draw 10 lines dividing the total distance between 7 and 8 into 10 equal parts.

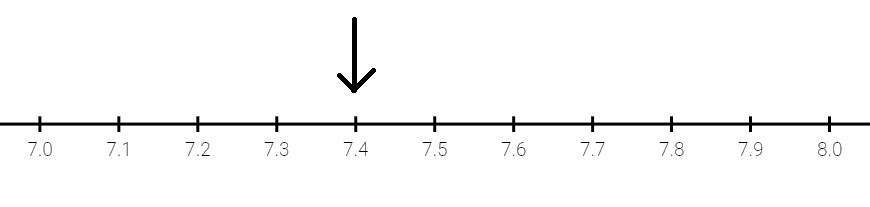
We can see that the arrow is four parts to the right of the whole number 7.

Similarly, to represent 7.45 on a number line, we first draw 10 lines dividing the total distance between 7.4 and 7.5 into 10 equal parts.

The steps that we used above to represent a thousandth on a number line can be summarised as  –

1. We draw a number line between 0 and 1.
2. We then draw 10 lines dividing the total distance between 0 and 1 into 10 equal parts.
3. Now, one whole divided into 10 parts is equal to  $\frac{1}{10}$.
4. $\frac{1}{10}$ in decimal form is equal to 0.1.
5. At each new line, we are adding $\frac{1}{10}$ or 0.1.
6. So, between 0 and 1 we have, 0 . 1 , 0 . 2 , . 0 . 3 , 0 . 4 , 0 . 5 , 0 . 6 , 0 . 7 , 0 . 8 and 0 . 9. Similarly, between 1 and 2 we have, 1 . 1 , 1 . 2 , 1 . 3 , 1 . 4 , 1 . 5 , 1 . 6 , 1 . 7 , 1 . 8 and 1 . 9.
7. We can also say that the line representing $\frac{1}{2}$ or 0.5 is the half way mark between 0 and 1. Similarly, the line representing $1\frac{5}{10}$ or 1.5 is the half way mark between 1 and 2.
8. Ten tenths is equal to one whole.
9. Next, we perform the same steps to draw 10 lines dividing the total distance between 0.01 and 0.02 into 10 equal parts.
10. In this manner, we can plot the hundredths of a decimal on a number line.

The above process can be defined as – “To represent a hundredths on a number line, we will first have to divide the distance between two whole numbers into 10 equal parts to get their tenths values. Next, we divide again the distance between two tenths to get their hundredths values.” 

Representing Thousandths on a Number Line

Let us now represent thousandths of a decimal on a number line. But, let us recall what we means by thousandths of a decimal?

If an object is divided into 1000 equal parts, then each part is one thousandth of the whole. This means that –

One thousandth = $\frac{1}{1000}$ which in decimal form is equal to 0.001

If we take 7 parts out of 1000 equal parts of an object, then 7 parts make $\frac{7}{1000}$ of the whole and it is written as 0.007.

Now, let us represent thousandths on a number line. We can understand this by an example.

Let us represent the thousandth value of the number 7.456 on a number line. 

To represent 7.4 on a number line, we first draw 10 lines dividing the total distance between 7 and 8 into 10 equal parts.

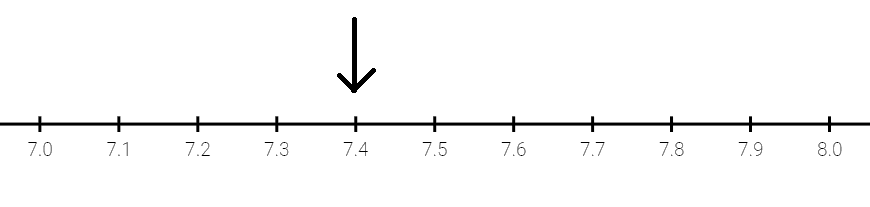
We can see that the arrow is four parts to the right of the whole number 7.

Similarly, to represent 7.45 on a number line, we first draw 10 lines dividing the total distance between 7.4 and 7.5 into 10 equal parts.

We can see that the arrow is five parts to the right of the decimal number 7.40.

Next, to represent 7.456 on a number line, we first draw 10 lines dividing the total distance between 7.45 and 7.46 into 10 equal parts.

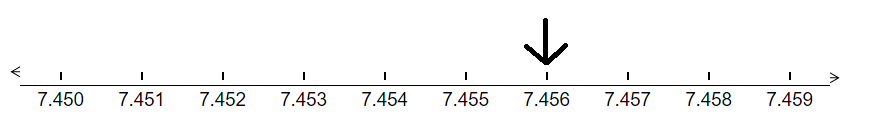
We can see that the arrow is six parts to the right of the decimal number 7.45

So, in this manner, we have represented the number 7.456 on the number line.

The steps that we used above to represent a thousandth on a number line can be summarised as  –

11. We draw a number line between 0 and 1.
12. We then draw 10 lines dividing the total distance between 0 and 1 into 10 equal parts.
13. Now, one whole divided into 10 parts is equal to  $\frac{1}{10}$.
14. $\frac{1}{10}$ in decimal form is equal to 0.1.
15. At each new line, we are adding $\frac{1}{10}$ or 0.1.
16. So, between 0 and 1 we have, 0 . 1 , 0 . 2 , . 0 . 3 , 0 . 4 , 0 . 5 , 0 . 6 , 0 . 7 , 0 . 8 and 0 . 9. Similarly, between 1 and 2 we have, 1 . 1 , 1 . 2 , 1 . 3 , 1 . 4 , 1 . 5 , 1 . 6 , 1 . 7 , 1 . 8 and 1 . 9.
17. We can also say that the line representing $\frac{1}{2}$ or 0.5 is the half way mark between 0 and 1. Similarly, the line representing $1\frac{5}{10}$ or 1.5 is the half way mark between 1 and 2.
18. Ten tenths is equal to one whole.
19. Next, we perform the same steps to draw 10 lines dividing the total distance between 0.01 and 0.02 into 10 equal parts.
20. Again, we perform the same steps to draw 10 lines dividing the total distance between 0.001 and 0.002 into 10 equal parts.
21. In this manner, we can plot the thousandth of a decimal on a number line.

The above process can be defined as – “To represent a thousandth on a number line, we will first have to divide the distance between two whole numbers into 10 equal parts to get their tenths values. Next, we divide again the distance between two tenths to get their hundredths values. Finally, we divide the distance between two hundredths into 10 equal parts to get their thousandths values.” 

Solved Examples

Example 1 Between what two numbers is does the decimal number 5.4 lie on the number line?

Solution We have been given the decimal number 5.4 and we need to check between which two whole numbers will it lie.

On observing the number 5.4 we can see that the number represents a tenth of a decimal as it has one digit after the decimal point.

Also, we know that 5.4 = 5 + $\frac{4}{10}$

This means that 5.4 is equal to 5 whole parts plus 4 tenths. Et us plot it on the number line. we will have,

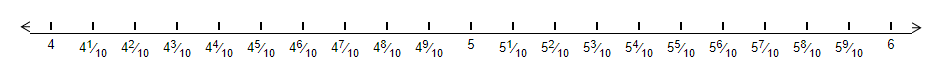
We can clealry see that 5.4 will lie between 5 and 6. The point on the number line will be – 

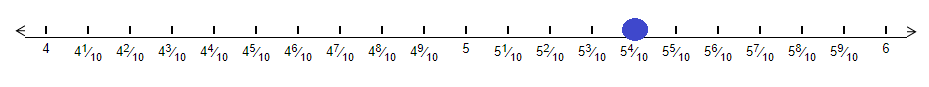
Hence, we can say that the number 5.4 will be between the whole numbers 5 and 6.

Example 2 Label the missing decimal numbers on the number line.

Solution We have been given four numbers marked as A , B , C and D on a number line and we need to find out which decimal numbers they represent. Let us mark them one by one.

We will start with completing the marking of the lines that have not been marked on the given number line. It can be clearly seen that there are 10 lines between two whole numbers on the number line. This means that the lines represent one tenth of the number in the decimal form. Therefore, the lines between 7 and 8 will be marked as  7 . 1 , 7 . 2 , 7 . 3 , 7 . 4 , 7  5 , 7 . 6 , 7 . 7 , 7 . 8 and d 7. 9. Similarly, We between the whole numbers 8 and 9 we have,  8 . 1 , 8 . 2 , 8 . 3 , 8 . 4 , 8 . 5 , 8 . 6 , 8 . 7 , 8 . 8  and 8 . 9. The number line so obtained will be – 

Now, we shall check the position of the four points on this number line. 

We can see that from the number line above, the point A lies on the decimal number 8.7. Hence A = 8 . 7

Now, let us check the position of point B. 

We can see that from the number line above, point B lies on the decimal number 8.2. Hence B = 8 . 2

Now, let us check the position of point C. 

We can see that from the number line above, point C lies on the decimal number 7 . 1. Hence C = 7 . 1

Now, let us check the position of point D. 

We can see that from the number line above, the point D lies on the decimal number 7 . 8 . Hence D =  7 . 8 

Therefore, we have,

A = 8 . 7

B = 8 . 2

C = 7 . 1

D =  7 . 8

Key Facts and Summary

1. A decimal indicates a part of a whole.
2. A number line is a straight horizontal line with numbers placed at even intervals that provides a visual representation of numbers.
3. Representing decimal on a number line is defined as the plotting of decimal numbers on a number line.
4. To represent a tenth on a number line, we will first have to divide the distance between two whole numbers into 10 equal parts to get their tenth values. Next, we plot the tenth values that lie between the whole part.
5. To represent a hundredth on a number line, we will first have to divide the distance between two whole numbers into 10 equal parts to get their tenth values. Next, we divide again the distance between two tenths to get their hundredths values.
6. To represent a thousandth on a number line, we will first have to divide the distance between two whole numbers into 10 equal parts to get their tenth values. Next, we divide again the distance between two tenths to get their hundredths values. Finally, we divide the distance between two-hundredths into 10 equal parts to get their thousandths values.