Introduction
If a and b are natural numbers such that a > b, then the equation x + a = b is not solvable in N, the set of natural numbers. This means that there is no natural number satisfying the equation x + a = b. so, the set of natural numbers is extended to form the set I of integers in which every equation of the form x + a = b, for a and b being natural numbers is solvable. However, the equations of the form x a = b, where a ≠ 0 and a and b being integers are not solvable for I also. Hence, the set I of integers is extended to obtain the set Q of all rational numbers in which every equation of the form x a = b, where a ≠ 0 and a and b being integers are solvable. But, the equations of the form x 2 = 2, x 2 = 3 etc. are not solvable in Q because there is no rational number whose square is 2. Such numbers are known as irrational numbers. The set Q of all rational numbers is extended to obtain the set of R of real numbers that include both rational and irrational numbers. However, the equations of the form x 2 + 1 = 0, x 2 + 4 = 0, etc. are not solvable in R which means that there is no real number whose square is a negative real number. Euler was the first mathematician to introduce the symbol i ( iota ) for the square of – 1, i.e. a solution of x 2 + 1 = 0 with the property i 2 = – 1. He also called this symbol as the imaginary unit. This gave the concept of complex numbers and the complex plane. Let us learn more about them.
Definition
If a, b are two real numbers, then a number of the form a + i b is called a complex number. For example, 7 + 2 I, – 1+ I, 3 – 2 I, 0 + 2 I are complex numbers. Real and imaginary parts of a complex number: If z = a + i b is called a complex number, then “ a “ is called the real part of z and “ b “ is known as the imaginary part of z. the real part of z is denoted by Re ( z ) and the imaginary part of z is denoted by Im ( z ). The complex plane is named after a Paris-based amateur mathematician Jean-Robert Argand (1768 – 1822).
Modulus of a Complex Number
The modulus of a complex number z = a + i b is denoted by | z | and is defined as
| z | = $\sqrt{a^2+ b^2} = \sqrt{{ Re ( z )}^2 + { Im ( z )}^2}$
From above we can see that | z | ≥ 0 for all z ∈ C.
What is a complex plane?
The complex plane (also known as the Gauss plane or Argand plane) is a geometric method of depicting complex numbers in a complex projective plane. Let us learn more about the complex plane
Geometrical representation of a complex number ( Argand Plane )
A complex number z = x + i y can be represented by a point ( x, y ) on the plane which is known as the Argand plane. To represent z = x + i y in geometric form, we take mutually perpendicular straight lines. Now we will plot a point whose x and y coordinates are represented by the real and the imaginary parts of z. This point P ( x, y ) represents the complex number z = x + i y. Below is the geometric representation of the point P ( x, y ) on the complex plane.
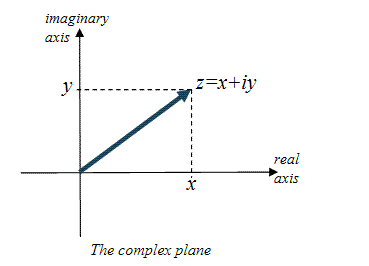
Some important points to remember here are –
- If the complex number is purely real, then its imaginary part will be 0. This means that a purely real number will be represented by a point on the x – axis. This is why x – the axis is known as the real axis.
- If the complex number is purely imaginary, then its real part will be 0. This means that a purely imaginary number will be represented by a point on the y – axis. This is why y-axis is known as the imaginary axis.
- If P ( x, y ) is a point on the complex plane, then the point P ( x, y ) represents a complex number z = x + i y. the complex number z = x + i y is known as the affix of the point P.
- The plane in which we represent a complex number in geometrical form is known as the complex plane or Argand plane or the Gaussian plane. The point P plotted on the Argand plane is called the Argand diagram.
Multiplication of Complex Numbers
Let us now understand the multiplication of complex numbers. For this purpose let us consider two complex numbers, say, z1 = ( a + i b ) and z2 = ( c + i d ). Let us how we can multiply these two complex numbers.
Since we need to multiply z1 and z2, we will have,
z1 x z2 = ( a + i b ) ( c + i d ) . . . . . . . . . . . . . . . . . . . . . . . . . ( 1 )
⇒ z1 x z2 = a c + i ( a d ) + i ( b c ) + i 2 ( b d )
We know that i 2 = – 1 , therefore, substituting the value of i 2 in the above equation, we will have,
z1 x z2 = a c + i ( a d ) + i ( b c ) + ( – 1 ) ( b d )
Now, we will combine the real numbers with the imaginary numbers, we will get,
z1 x z2 = ( a c – b d ) + i ( a d + b c ) . . . . . . . . . . . . . . . . ( 2 )
So, we can say that for any two complex numbers, z1 = ( a + i b ) and z2 = ( c + i d ), z1 x z2 = ( a c – b d ) + i ( a d + b c )
Let us now discuss the associative property of multiplication of complex numbers.
What is associative property?
Associative Property states that when an operation is performed on more than two numbers, the order in which the numbers are placed does not matter. In the case of multiplication, this means that if we want to multiply 3 numbers, two of them can be chosen first, one as a multiplier and the second as a multiplicand. The result of the multiplication would serve as a multiplier and the third number as a multiplicand to get the final answer. Is multiplication of complex numbers associative? Let us find out.
Is multiplication of complex numbers associative?
For verifying the associative property of multiplication of complex numbers, let us consider three complex numbers.
So, let z 1 = a + i b, z 2 = c + i d and z 3 = e + i f be any three complex numbers. Then in order for the multiplication of these complex numbers to be associative, the following statement should be true –
( z 1 z 2 ) z 3 = z 1 ( z 2 z 3 )
Let us verify the above statement using the three complex numbers, z 1 = a + i b, z 2 = c + i d and z 3 = e + i f
So, we have,
( z 1 z 2 ) z 3 = { ( a + i b ) ( c + I d ) } ( e + i f )
= { ( a c – b d ) + i ( a d + c b ) } ( e + i f )
= { ( a c – b d ) e – ( a d + c b ) f ) + i { ( a c – b d ) f + ( a d + c b ) e )
= { a ( c e – d f ) – b ( c f + e d ) } + i { b ( c e – d f ) + a( e d + c f )
= ( a + i b ) { ( c f – d f ) + i (c f + e d ) }
= z 1 ( z 2 z 3 )
Hence, for any three complex numbers, z 1 = a + i b, z 2 = c + i d and z 3 = e + i f, we have,
( z 1 z 2 ) z 3 = z 1 ( z 2 z 3 )
Hence, we can say that the multiplication of complex numbers satisfies the associative property.
Verifying the associative property of multiplication of complex numbers as ordered pair
By the definition of complex numbers, the complex numbers, x, y, z ∈ C are identified by ordered pairs x = ( a, b ), y = ( c, d ) z = ( e, f ) for some real numbers a, b, c, d, e, f ∈ R
So, for the ordered pairs to be associative, we need to show that
( x . y ) . z = x . ( y . z )
We have,
( x . y ) . z = [ ( a , b ) ⋅ ( c , d ) ] ⋅ ( e , f ) ( by definition of complex numbers )
⇒ ( x . y ) . z = ( a c – b d , a d + b c ) ⋅ ( e , f ) ( by definition of multiplication of complex numbers )
⇒ ( x . y ) . z = ( ( a c – b d ) e − ( a d + b c ) f , ( a c – b d ) f + ( a d +b c ) e ) (by definition of multiplication of complex numbers )
⇒ ( x . y ) . z = ( ( a c e – b d e ) − ( a d f + b c f ) , ( a c f – b d f ) + ( a d e + b c e ) ) ( by distributive law of real numbers )
⇒ ( x . y ) . z = ( a c e – b d e – a d f – b c f , a c f – b d f + a d e + b c e ) ( by distributive law of real numbers and associativity of addition )
⇒ ( x . y ) . z = ( a c e – a d f – b c f – b d e , a c f + a d e + b c e – b d f ) ( by commutativity of addition of real numbers )
⇒ ( x . y ) . z = ( ( a c e – a d f ) − ( b c f + b d e ) , ( a c f + a d e ) + ( b c e – b d f ) ) (by distributive law of real numbers )
⇒ ( x . y ) . z = ( a ( c e – d f ) – b ( c f + d e ) , a ( c f + d e ) + b ( c e – d f ) ) ( by distributive law of real numbers )
⇒ ( x . y ) . z = ( a , b ) ⋅ ( c e – d f , c f + d e ) ( by definition of multiplication of complex numbers )
⇒ ( x . y ) . z = ( a , b ) ⋅ [ ( c , d ) ⋅ ( e , f ) ] ( by definition of multiplication of complex numbers )
⇒ ( x . y ) . z = x ⋅ ( y ⋅ z ) ( by definition of complex numbers )
Hence, we can say that the multiplication of ordered pairs of complex numbers satisfies the associative property.
Key Facts and Summary
- If a, b are two real numbers, then a number of the form a + i b is called a complex number.
- If z = a + i b is called a complex number, then “ a “ is called the real part of z and “ b “ is known as the imaginary part of z. the real part of z is denoted by Re ( z ) and the imaginary part of z is denoted by Im ( z ).
- The modulus of a complex number z = a + i b is denoted by | z | and is defined as
| z | = $\sqrt{a^2+ b^2} = \sqrt{{ Re ( z )}^2 + { Im ( z )}^2}$ - The complex plane (also known as the Gauss plane or Argand plane) is a geometric method of depicting complex numbers in a complex projective plane.
- A complex number z = x + i y can be represented by a point ( x, y ) on the plane which is known as the Argand plane.
- If the complex number is purely real, then its imaginary part will be 0. This means that a purely real number will be represented by a point on the x – axis. This is why x – axis is known as the real axis.
- If the complex number is purely imaginary, then its real part will be 0. This means that a purely imaginary number will be represented by a point on the y – axis. This is why y – axis is known as the imaginary axis.
- If P ( x, y ) is a point on the complex plane, then the point P ( x, y ) represents a complex number z = x + i y. the complex number z = x + i y is known as the affix of the point P.
- The plane in which we represent a complex number in geometrical form is known as the complex plane or Argand plane or the Gaussian plane. The point P plotted on the Argand plane is called the Argand diagram.
- So, we can say that for any two complex numbers, z1 = ( a + i b ) and z2 = ( c + i d ), z1 x z2 = ( a c – b d ) + i ( a d + b c )
- Associative Property states that when an operation is performed on more than two numbers, the order in which the numbers are placed does not matter.
- For any three complex numbers, z 1 = a + i b, z 2 = c + i d and z 3 = e + i f, we have, ( z 1 z 2 ) z 3 = z 1 ( z 2 z 3 )
Recommended Worksheets
Complex Fractions (Fashion Themed) Worksheets
Multiplication Property (Valentine’s Day Themed) Math Worksheets
Multiplication Tables (St. Patrick’s Day Themed) Math Worksheets









