Introduction
Simple interest affects people in various aspects of their financial life, like when borrowing money, depositing, or investing money, and lending money.
This article will define simple interest, explain how to compute it for loans or investments, compare simple and compound interests, and solve more simple interest-related situations.
What is simple interest?
Definition
Simple interest is a way to calculate how much interest will be charged on a sum of money at a specific rate and for a particular time duration. The interest rate will not be modified by any interest accrued; it will only apply to the principal amount of the loan or investment.
Simple interest is computed annually as a percentage of the principal sum. The annual interest rate, the duration of the investment or loan, and the principal amount are multiplied to determine simple interest.
What is the Simple Interest Formula?
If you know the principal amount, the rate of interest, and the time duration, you can use the simple interest formula to calculate the interest. The simple interest formula is given as:
Simple interest: I = P × R × T
where;
I = the simple interest or the amount charged on a sum of money at a specific rate and for a particular time duration
P = the principal amount, or the initial amount borrowed or invested
R = the rate of interest (per annum), which is given in percentage and converted to decimal in the calculation
T = the time (in years) or the duration for which the principal amount is given to someone.
The following formulas are also used when the missing values are the principal amount, rate of interest, or time.
| when P is missing | when R is missing | when T is missing |
| $P=\frac{I}{R×T}$ | $R=\frac{I}{P×T}$ | $T=\frac{I}{P×R}$ |
We use the formulas below to calculate the amount of money paid back at the end of the given time.
Amount=Principal+Interest
or
A=P+I
Where;
A = total amount
P = principal
I = Interest
The following are other formulas to use when calculating the total amount.
A=P+(PRT)
A=P(1+ RT)
where;
A = total amount
P = principal
R = Rate of Interest (per annum)
T = Time (in years)
Calculating Simple Interest
Example 1
The bank granted Ted’s mother a \$1,000 loan at a 5% interest rate. If the amount is borrowed for a year, what would the simple interest be? Determine the simple interest if the loan amount is borrowed for 4, 5, or 10 years.
Solution:
Let us first convert the given rate of interest to decimal. Hence, we have,
5%×$\frac{1}{100}$=0.05
The simple trick to converting percentage to decimal is to move the decimal point of the rate two places to the left.
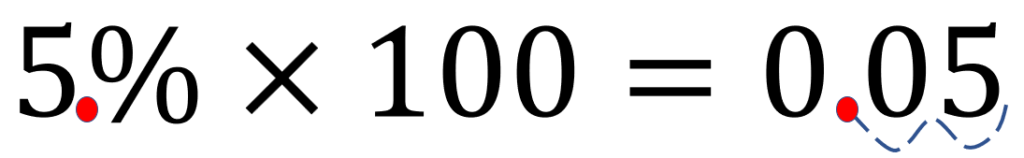
Let us now use the formula I=PRT to calculate the simple interest for a year, four years, five years, and ten years.
| Simple interest when t = 1 year I = P × R × T I = \$1000 × 0.05 × 1 I = \$50 | Simple interest when t = 5 years I = P × R × T I = \$1000 × 0.05 × 5 I = \$250 |
| Simple interest when t = 4 years I = P × R × T I = \$1000 × 0.05 × 4 I = \$200 | Simple interest when t = 10 years I = P × R × T I =\$1000 × 0.05 × 10 I = \$500 |
Hence, the simple interest for 1 year is \$50, for 4 years is \$200, for 5 years is %250, and for 10 years is \$500.
We can also solve for the total amount that Ted’s mother needs to return to the bank after each time duration.
| Amount when t = 1 year Amount = P + I A = \$1000 + \$50 A= \$1050 | Amount when t = 5 years A = P + I A = \$1000 + \$250 A = \$1250 |
| Amount when t = 4 years A = P + I A = \$1000 + \$200 A = \$1200 | Amount when t = 10 years A = P + I A = \$1000 + \$500 A = \$1500 |
Example 2
A total of \$1,500 is invested for 2 years at a simple interest rate of 6%. How much interest does this investment yield?
Solution:
The principal amount here is \$1500, the time is 2 years, and the rate of interest is 6% or 0.06. To calculate the interest earned in 2 years, we have,
I = P × R × T
I = \$1500 × 0.06 × 2
I = \$180
Hence, the interest earned for 2 years for this investment is \$180.
Example 3
How much simple interest will Dianne pay if she takes out a loan for \$25,000 for three years at 15% per year?
Solution:
Let us use \$25000 as P, T = 3 years, and R = 15% or 0.15. Hence, we have the computation below,
I = P × R × T
I = \$25000 × 0.15 × 3
I = \$11250
Therefore, Diane will pay an interest of \$11250.
More Examples
The following examples are word problems where the simple interest is known, but it is necessary to calculate the rate of interest, principal amount, period, or total amount.
When R (rate of interest is missing)
Example 1
After two years, a woman with \$50000 in a bank received \$5000 in interest on her investment. Find the interest rate that was paid on the money that was deposited.
Solution:
Let us have P = \$50000, I = \$5000 and T = 2 years. To find the rate of interest, we have,
R=$\frac{I}{P×T}$
R=$\frac{\$5000}{\$50000 ×2}$
R=$\frac{\$5000}{\$100000}$
R=0.05=5%
Therefore, the rate of interest applied to the woman’s investment was 5% per annum.
Example 2
Find the simple rate given a principal amount of \$25000, with an interest of \$1000, and over 2 years.
Solution:
Given: P = \$2500 , T = 4 years, and I = \$1000.
Let us substitute the given information for the formula. Hence, we have,
R=$\frac{I}{P×T}$
R=$\frac{\$1000}{\$2500 ×4}$
R=$\frac{\$1000}{\$10000}$
R=0.01=10%
In this case, the interest rate is 10% over a two-year period for a principal of \$25,000 and an interest of \$1,000.
Example 3
Stephanie took out a loan from the bank for \$5200, and they charged her \$182 in simple interest over a year.
( a ) Determine the loan’s applied interest rate.
( b ) Calculate the total amount that she must pay to the bank, including the principal and interest.
Solution:
Let us first determine the loan’s applied interest rate given that P = \$5200, I =182, and T = 1 year.
( a ) Substituting the given values to the formula, we will have,
R=$\frac{I}{P×T}$
R=$\frac{\$182}{\$5200 ×1}$
R=$\frac{\$182}{\$5200}$
R=0.035=3.5%
( b ) To calculate the total amount that Stephanie needs to pay to the bank, we will utilize the formula A=P+I; thus, we have,
A=P+I
A=\$5200+\$182
A=\$5382
As a result, Stephanie must pay the bank a total of \$5382 for her loan, which has a \$5200 principal and 3.5% annual interest.
When P (principal amount) is missing
Example 1
Martha invested in a bank that earned her \$900 for three years with a simple interest of 6% per annum. How much did Martha deposit?
Solution:
Since the missing in this problem is the principal amount, we will use the formula: R=$\frac{I}{P×T}$. The known values are I = \$900, R = 6%, and T = 3 years.
Let us now substitute the given values for the formula.
R=$\frac{I}{P×T}$
P=$\frac{\$900}{0.06×3}$
P=$\frac{\$900}{0.18}$
P=\$5000
Therefore, Martha made an initial deposit of \$5000, which paid her \$900 over three years at a simple rate of 6%.
Example 2
Consider taking out a 5-year loan from a bank at an 8% annual interest rate.
( a ) Determine the principal amount you borrowed if the simple interest is \$200.
( b ) Calculate the total amount (principal + interest) that must be returned after the given period.
Solution:
In this problem, we have the following data: Time = 5 years, Interest = \$1200, and Rate = 8%
If we convert 8% to decimal will give us 0.08. Now, plug the data into the formula to find the principal amount.
( a ) Determine the principal amount you borrowed if the simple interest is \$1200.
R=$\frac{I}{P×T}$
P=$\frac{\$1200}{0.08×5}$
P=$\frac{\$1200}{0.4}$
P=\$3000
Therefore, the principal amount is \$3000 when the simple interest is \$1200 of a loan with an 8% rate for 5 years.
( b ) Calculate the total amount (principal + interest) that must be returned after the given period.
Since we already know the principal and the interest, let us substitute the value to the formula and get the sum. So, we have,
A = P + I
A = \$3000 + \$1200
A = \$4200
Hence, the total amount is \$4200.
When T (time) is missing
Example 1
Edward took out a \$1500 loan at a 12% annual interest rate to pay for a new phone. Find the loan’s term in years if the simple interest is \$360. How much will Edward pay overall?
Solution:
The information that we have are P = \$1500, R = 12%, and I = \$360. The rate of interest of 12% is equal to 0.12 in decimal. So, substituting the values to the formula to find T or the loan’s term, we have,
$T=\frac{I}{P×R}$
T=$\frac{\$360}{\$1500×0.12}$
T=$\frac{\$360}{\$180}$
T=2 years
To calculate the amount that Edward needs to pay overall, we have,
A = P + I
A = \$1500 + \$360
A = \$1860
Thus, Edward needs to pay an overall amount of \$1860.
Example 2
Marites just had an investment mature, and she received \$9000 in simple interest on a \$12,000 principal. Determine how many years she held the investment if the rate of interest was 15% per year.
Solution:
To determine how long Marites held the money, let us substitute the specified values in the formula.
Given: P = \$12000 , I = \$9000, and R = 15% = 0.15
$T=\frac{I}{P×R}$
T=$\frac{\$9000}{\$12000×0.15}$
T=$\frac{\$9000}{\$1800}$
T=5 years
Therefore, Marites held the investment for five years.
When T is not given in years
Example 1
Jared intends to invest his money in a security with a six-month maturity. Find the simple interest he will receive over the next six months if his principal is \$4,000 and interest is generated at a rate of 5% per year.
Solution:
In this case, the given are as follows:
P = \$4000, T = 6 months, and R = 5% or 0.05.
Notice that the holding period is just 6 months; in the formula, time must be in years. Given that there are 12 months in a year, time (T) must be calculated as,
T=$\frac{6}{12}=\frac{1}{2}$ or 0.5
Let us now substitute the given into the formula to calculate the simple interest.
I = P × R × T
I = \$4000 × 0.05 × 0.5
I = \$100
Hence, Jared will earn a simple interest of \$100 in 6 months.
Example 2
A bank is offering 2.5% simple interest on a savings account. If you deposit \$7000, how much interest will you earn in 2 years and 3 months?
Solution:
Given: P = \$7000 , T = 2 years and 3 months, and R = 2.5% or 0.025
Since the given time is 2 years and 3 months, let us convert 3 months to years by dividing it by 12. So, we have,
$\frac{3}{12}=\frac{1}{4}$=0.25 years
The total time to use is ( 2 + 0.25 ) years or 2.25 years.
Let us now calculate the simple interest by substituting the known values into the formula.
I = P × R × T
I = \$7000 × 0.025 × 2.25
I = \$393.75
Therefore, the interest earned after holding the money for 2 years and 3 months is \$393.75.
When A (principal + interest) is missing
Example 1
Richard borrowed \$4000 with a rate of interest of 6% per year. Calculate the following:
( a ) Simple interest and the total amount in one (1) year
( b ) Simple interest and the total amount in three (3) years
( c ) Simple interest total amount in five (5) years
Solution:
( a ) Simple interest and the total amount in one (1) year
Let us first compute the simple interest, then add the quantity to the principal amount. Hence, we have,
Given: P = \$4000, R = 6% = 0.06, T = 1 year
I=P × R × T
I=\$4000 × 0.06 × 1
I= \$240
Using the formula A=P+I,
A = \$4000 + \$240
A = \$4240
Alternative solutions
| A = P+( PRT ) A = \$4000 + (\$4000 × 0.06 × 1 ) A = \$4000 + \$240 A = \$4240 | A = P( 1+ RT ) A = \$4000 ( 1 + 0.06⋅1 ) A = \$4000 ( 1 + 0.06 ) A = \$4000 ( 1.06 ) A = 4240 |
Therefore, the simple interest is \$240, and the amount that must be paid back after a year must be \$4240.
( b ) Simple interest and the total amount in three (3) years
Given: P = \$4000, R = 6% = 0.06, T = 3 years
I = P × R × T
I = \$4000 × 0.06 × 3
I = \$720
To find the total amount that needs to be paid back after a year, we use the formula A=P+I,
A = \$4000 + $720
A = \$4720
Alternative solutions
| A = P+( PRT ) A = \$4000 + ( \$4000 × 0.06 × 3 ) A = \$4000 + \$720 A = \$4720 | A = P( 1+ RT ) A = \$4000 ( 1 + 0.06⋅3 ) A = \$4000 ( 1 + 0.18 ) A = \$4000 ( 1.18 ) A = 4720 |
Therefore, the simple interest is \$720, and the amount that must be paid back after a year must be \$4720.
( c ) Simple interest and the total amount in three (5) years
Given: P = \$4000, R = 6% = 0.06, T = 5 years
I = P × R × T
I = \$4000 × 0.06 × 5
I = \$720
To find the total amount that needs to be paid back after a year, we use the formula A=P+I,
A = \$4000 + \$1200
A = \$5200
Alternative solutions
| A = P+( PRT ) A = \$4000 + ( \$4000 × 0.06 × 5 ) A = \$4000 + \$1200 A = \$5200 | A = P( 1+ RT ) A = \$4000 ( 1 + 0.06⋅5 ) A = \$4000 ( 1 + 0.3) A = \$4000 ( 1.3 ) A = 5200 |
Therefore, the simple interest is \$1200, and the amount that must be paid back after a year must be \$5200.
Simple Interest vs Compound Interest
When a person borrows money, there is a price they must pay the lender called interest. It is common to indicate interest as a percentage, which can be either simple or compound. Two methods for calculating interest on a loan amount are simple interest and compound interest. Because of some fundamental distinctions between the two, compound interest is thought to be more challenging to compute than simple interest. What differentiates simple interest from compound interest is primarily that simple interest is based on the principal amount of a deposit or loan, whereas compound interest is based on the principal amount and interest that accrues over time.
Let us use the following table to compare simple interest with compound interest:
| Simple Interest | Compound Interest |
| The principal amount, rate of interest, and length of the loan are multiplied to determine simple interest. | The principal balance plus any accrued interest constitutes the basis for compound interest. |
| The same principal amount is the basis for the interest, which is the same each year. | Interest grows over time. |
| The principal amount stays the same each year. | The amount at the end of a year acts as the principal for the following year. |
| Growth continues to be consistent. | The growth picks up quickly. |
| Simple Interest Formula I=P×R×T | Compound Interest Formula I=P (1+R)t – P |
Summary
Simple interest is a way to calculate how much interest will be charged on a sum of money at a specific rate and for a particular time duration. The interest rate will not be modified by any interest accrued; it will only apply to the principal amount of the loan or investment.
When calculating simple interest, the rate of interest must be converted to decimal, and if the time spans over months, it must be converted to years.
Formulas
Simple Interest: I=P×R×T
where I = simple interest, P = principal amount, R = rate of interest, and T is the duration of time.
| when P is missing | when R is missing | when T is missing |
| P=$\frac{I}{R×T}$ | R=$\frac{I}{P×T}$ | T=$\frac{I}{P×R}$ |
We use the formulas below to calculate the amount of money paid back at the end of the given time.
A=P+I
Where;
A = total amount
P = principal
I = Interest
Alternative Formulas
A=P+(PRT)
A=P(1+ RT)
Frequently Asked Questions on Simple Interest (FAQs)
How do you calculate simple interest?
Simple interest is a way to calculate how much interest will be charged on a sum of money at a specific rate and for a particular time duration. The formula that we use in calculating simple interest is I=P×R×T.
Let us say, for example, that a person takes out a loan of \$2000 at a rate of 10% annually for 3 years. The simple interest will then be,
I = P × R × T
I = \$2000 × 0.10 × 3
I = \$600
What is the most typical application for simple interest?
Simple interest is a way to calculate the amount of interest that will be charged on a sum of money at a specified rate and for a specific amount of time; it is frequently used in financial transactions, including saving, borrowing, and investing. Short-term loans, such as auto loans, instalment loans, personal loans, and some types of mortgages, are included in the borrowing transactions.
How do simple interest and compound interest differ from one another?
Two methods for calculating interest on a loan amount are simple interest and compound interest. Because of some fundamental distinctions between the two, compound interest is thought to be more challenging to compute than simple interest. What differentiates simple interest from compound interest is primarily that simple interest is based on the principal amount of a deposit or loan, whereas compound interest is based on the principal amount and interest that accrues over time.
Recommended Worksheets
Simple Interest (International Day of Banks Themed) Math Worksheets
Compound Interest ( National Financial Literacy Month Themed) Math Worksheets
Percents and Discounts (Thanksgiving Themed) Math Worksheets









