Negative and Positive Rules

What are integers?

An integer is a number that can be written without a fractional component. In other words, an integer is a whole number that can be positive, negative, or zero. Hence, we can say that integers are the collection of whole numbers and negative numbers. The set of integers is represented by Z and can be written as – 

Z = { …….. – 3, – 2 , – 1 , 0 , 1 , 2 , 3 …….. }

What are negative and positive integers?

Corresponding to natural numbers, 1, 2, 3, 4, 5 …… etc, we create new numbers, -1, -2, -3, -4 ,-5 and so on. These numbers are called minus one, minus two, minus three etc. such that – 

1 + ( – 1 ) = 0

2 + ( – 2 ) = 0

3 + ( – 3 ) = 0

So, – 1 is called the negative of 1, -2 is called the negative of 2 and each negative number is the opposite of its positive counterpart. If we combine these negative numbers with the positive ones, together we get a set of numbers which we call integers.

The numbers, 1, 2, 3, 4 ….. are natural numbers and are called positive integers while the numbers – 1, – 2 , – 3 etc. are called negative integers. 

The symbol for Negative Integers

We use the symbol “ – “ to denote negative integers and the same symbol is used to indicate subtraction. However, the context in which this symbol is used makes it clear, whether we mean to use it for a negative integer or subtraction. Let us understand it through an example.

Suppose we write the number – 5. This will be rea as “ minus five “. Similarly, – 17 will be read as “ minus seventeen “.

Now, let us write 5 – 3. We can see here that the “ – “ is between two numbers. This will be read as “ five minus three “. Hence, here the symbol has been used for the subtraction of two numbers.

The symbol for Positive Integers

We use the symbol “ + “ to denote positive integers and the same symbol is used to indicate addition. However, the context in which this symbol is used makes it clear, whether we mean to use it for a positive integer or addition. Let us understand it through an example.

Suppose we write the number + 5. This will be read as “ plus five “. Similarly, + 17 will be read as “ plus seventeen “.

Now, let us write 5 + 3. We can see here that the “ + “ is between two numbers. This will be read as “ five plus three “. Hence, here the symbol has been used for the addition of two numbers.

It is important to note here if no sign is associated with a number, it is read as a positive number. For instance, + 5 can also be written as simply 5. 

Negative and Positive Integers on a Number Line

We have learnt how to represent whole numbers on a number line. to represent integers on a number line. Recall that a number line is a straight horizontal line with numbers placed at even intervals that provides a visual representation of numbers. Primary operations such as addition, subtraction, multiplication, and division can all be performed on a number line. The numbers increase as we move towards the right side of a number line while they decrease as we move left. Integers are represented on a number line as shown below – 

Above is a visual representation of a standard number line for representing integers. As is clearly visible, as we move from left to right, there is an increase in the value of integers while it decreases when we move from right to left.

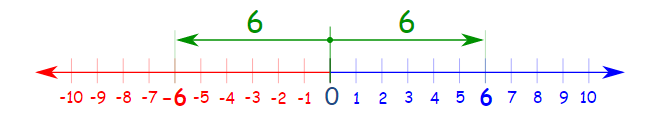
Let us understand it through an example

Let us plot 6 and – 6 on the number line.

Rules for the addition of positive and negative integers

We know how to add two whole numbers. We can add integers in the same manner with the only difference being that we have to perform the addition of negative numbers as well. the following rules are to be followed for the addition of integers – 

1. To add two positive integers or two negative integers, we add their absolute values and assign the sign of the addends to the sum.
2. To add a positive or a negative integer, we determine the difference of their absolute values and assign the sum of the addend having greater absolute value.

Let us understand it through an example.

Example

Suppose we have two integers, 1258 and 3214 and we want to find their sum.

Solution

First, we will check the sign of both numbers. We can see that both the numbers are of the same sign and are positive integers. Therefore, by the rules stated above, we will add the absolute value of both the numbers and assign a positive sign to them. We will have,

1258 + 3214 = 4473

Let us consider another example.

Suppose we have two integers, – 523 and 937 and we want to find their sum.

Solution

We can see that the integers to be added are of different signs, therefore, to add them we find the difference of their absolute values and assign the sign of the added having greater absolute value. We will thus have,

( – 5523 ) + 937 = 937 – 523 = 414

The above rules can be summarised as – 

Rules of Subtraction of positive and negative integers

We know how to subtract two whole numbers. It is important to recall that in whole numbers we cannot subtract a larger whole number from a smaller whole number. In the case of integers subtraction of integers, we can subtract a larger integer from a smaller integer. Also, it is important to recall that subtraction is a process inverse to that of addition.

The following rule is to be followed for the subtraction of integers – 

If a and b are two integers, then to subtract b from a, we change the sign of b and add it to a, i.e. a– b = a + ( – b ) 

Let us understand it using an example.

Example

Suppose we wish to subtract – 1235 from 4532

Solution

In order to subtract – 1235 from 4532, we will change the sign of – 1235 and add it to 4532. We will have,

4532 – ( – 1235 ) = 4532 + 1235 = 5767

Hence, 4532 – ( – 1235 ) = 5767

The above rules can be summarised as – 

Rules of Multiplication of positive and negative integers

We know that the process of finding out the product between two or more numbers is called multiplication and the result thus obtained is called the product. Multiplication of integers is similar to the multiplication of natural numbers and whole numbers, except for the fact that we have to take care of the multiplication of negative numbers as well.

The following rules are followed for the multiplication of integers – 

Case 1 – When you have two integers of opposite signs – The product of two integers of opposite signs is equal to the additive inverse of the product of their absolute values. This means that in order to find the product of a positive and negative integer we need to find the product of the absolute values and assign minus sign to the product. Let us understand it through an example. 

Example

Suppose you have two numbers 7 and -4 and wish to find the product. The multiplication of 7 and -4 will be given by 

7 x ( – 4 )  = – ( 7 x 4 ) = – 28

Similarly, ( – 6 ) x 9 = – ( 6 x 9 ) =  = – 54

Case 2 – The product of two integers with similar signs is equal to the product of their absolute values. This means that in order to find the product of two integers where whether both of the numbers are positive or both are negative, we will have to find the product of their absolute values. Let us understand this through an example.

Example

Suppose you have two numbers 7 and -4 and wish to find the product. The multiplication of – 7 and -4 will be given by 

( – 7 ) x ( – 4 )  =  ( 7 x 4 ) =  28

Similarly, (  6 ) x 9 =  ( 6 x 9 ) =  =  54

The above rules can be summarised as – 

Rules of Division of positive and negative integers

We know that Division is the process of repetitive subtraction. The same applies to the division of integers as well. There are four important terms in the division, namely, divisor, dividend, quotient, and the remainder. The formula for divisor constitutes all of these four terms. In fact, it is the relationship of these four terms among each that defines the formula for division. If we multiply the divisor with the quotient and add the result to the remainder, the result that we get is the dividend. This means,

Dividend = Divisor x Quotient + Remainder

Recall that a division of whole numbers is an inverse process of multiplication. Let us extend the same idea to the division of integers. The following rules are followed for the division of integers – 

Case 1 – The quotient of two integers both positive or negative is a positive integer equal to the quotient of the corresponding absolute values of the integers. This means that for dividing two integers with like signs we divide the values regardless of the sign and give a positive sign to the quotient. Let us understand it through an example. 

Example

Suppose you have two numbers  – 20 and -4 and wish to divide the first integer by the other. We will have,

-20 ÷ -4 = $\frac{20}{4}$ = 5

Case 2 – The quotient of a positive and negative integer is a negative integer and its absolute value is equal to the quotient of the corresponding absolute values of the integers. This means that when dividing integers with unlike signs we divide the value regardless of the sign and give minus sign to the quotient. Let us understand it through an example. 

Example

Suppose you have two numbers – 20 and 4 and wish to divide the first integer by the other. We will have,

-20 ÷ 4 = – $\frac{20}{4}$ = – 5

The above rules can be summarised as – 

Properties of negative and positive integers

Let us now discuss some of the properties of positive and negative integers – 

Closure Property

Closure property states that when an operation is performed on two numbers, the resultant would also be of the same type as the numbers on whom the operation has been performed. 

Hence, addition, subtraction and multiplication of positive as well as negative integers satisfy the closure property while the division of integers does not satisfy the closure property. 

Commutative Property 

Commutative Property states that when an operation is performed on two numbers, the order in which the numbers are placed does not matter. 

For any two integers, a  and b,

a + b = b +a

a – b ≠ b – a

a  x b = b x a

a ÷ b ≠ b ÷ a

Hence, the addition and multiplication of positive as well as negative integers satisfy the commutative property while subtraction and division of positive as well as negative integers do not satisfy the commutative property. 

Associative Property

Associative Property states that when an operation is performed on more than two numbers, the order in which the numbers are placed does not matter. 

For any three integers, a, b and c

a + ( b + c ) = ( a + b ) + c

a – ( b – c ) ≠ ( a – b ) – c

a x ( b x c ) = ( a x b ) x c

a ÷ ( b ÷ c ) ≠ ( a ÷ b ) ÷ c

Hence, addition and multiplication of positive as well as negative satisfy the associative property while subtraction and division of positive as well as negative do not satisfy the associative property. 

Distributive Property of Multiplication over Addition / Subtraction

When two positive or negative numbers are added or subtracted and the result is multiplied by another number, they can be multiplied separately.

Therefore, for any three integers, a, b and c, distributive property of multiplication over addition states that

a x ( b + c) = (a x b) + (a x c)

Similarly, for any three numbers, a, b and c, the distributive property of multiplication over subtraction states that

a x ( b – c) = (a x b) – (a x c)

For example, let us first consider 10 x (18 + 12)

We will use the distributive property of multiplication over addition.

We have 10 x (18 + 12)

 = (10 x 18) + (10 x 12)

 = 180 + 120

 = 300

Key Facts and Summary

1. An integer is a number that can be written without a fractional component.
2. The numbers, 1, 2, 3, 4 ….. are natural numbers and are called positive integers while the numbers – 1, – 2 , – 3 etc. ate called negative integers. 
3. We use the symbol “ – “ to denote negative integers and the same symbol is used to indicate subtraction.
4. We use the symbol “ + “ to denote positive integers and the same symbol is used to indicate addition.
5. The numbers increase as we move towards the right side of a number line while they decrease as we move left.
6. To add two positive integers or two negative integers, we add their absolute values and assign the sign of the addends to the sum.
7. To add a positive or a negative integer, we determine the difference of their absolute values and assign the sum of the addend having greater absolute value.
8. If a and b are two integers, then to subtract b from a, we change the sign of b and add it to a, i.e. a– b = a + ( – b ) 
9. The product of two integers of opposite signs is equal to the additive inverse of the product of their absolute values.
10. The product of two integers with similar signs is equal to the product of their absolute values.
11. The quotient of two integers both positive or negative is a positive integer equal to the quotient of the corresponding absolute values of the integers.
12. The quotient of a positive and negative integer is a negative integer and its absolute value is equal to the quotient of the corresponding absolute values of the integers.
13. Positive as well as negative integers satisfy the closure property. The addition and multiplication of positive as well as negative integers satisfy the commutative and associative properties. Subtraction and division of positive as well as negative integers do not satisfy the commutative and associative properties.

Recommended Worksheets

Integers (The Day of the Dead Themed) Math Worksheets
Understanding Commutative and Associative Property of Addition 1st Grade Math Worksheets
The Distributive Property and Algebraic Expressions 6th Grade Math Worksheets