Absolute Value | Definition, Examples, Symbol, Function & Properties

Introduction

We often come across the term absolute value in various situations. It is a commonly used term not just in the English language, but in mathematics as well. In mathematics, what do we mean by absolute value and how is it useful in different calculations. Let us find out.

Definition

The absolute value of a number refers to the distance of a number from the origin of a number line. However, an important here is that the absolute value of a number is not dependent upon the direction of the number. This means that the absolute value of the positive, as well as the negative part of a number, is the same. In other words, if the number is positive then it will result in a positive number only. And if the number is negative, then the modulus of this number will also be a positive number.

Symbol for absolute value

The symbol of absolute value is | x |, where x is an integer. It is important to note here that there is no absolute value for 0. This is because 0 has no sign and the absolute value of a number is dependent upon the sign of the number. Let us understand this by an example.

The absolute value of 4 is 4, i.e. | 4 | = 4

The absolute value of – 4 is 4, i.e. | – 4 | = 4

The absolute value of 5 is 5, i.e. | 5 | = 5

The absolute value of – 5 is 5, i.e. | – 5 | = 5

The above examples show that the absolute value of both positive, as well as negative numbers, will be a positive number only.

Absolute Value on a Number Line

Let us now discuss the representation of absolute value on a number line. We have already learnt that the absolute value of the positive, as well as the negative part of a number, is the same. How do we represent the same on a number line? Let us find out.

Consider the number 5. We have seen above that the absolute value of 5 is 5. This means that the distance of the number 5 from 0 is 5 units. The representation of the same on a number line will be as under –

Now, let us consider the number – 5. We have seen above that the absolute value of – 5 is 5. This means that the distance of the number – 5 from 0 is 5 units. The representation of the same on a number line will be as under –

We have seen above the representation of the absolute value of a number on a number line. Let us now discuss the representation of the absolute value of a sum of a number on a number line. For instance, let us have the sum of 2 and – 7. We know that since 2 and -7 are of opposite signs, therefore by the rules of operations on integers, the smaller number would be subtracted from the larger number and the result obtained would bear the sign of the larger number. In our case, it would be – 7 + 2 = – 5. Now, we have already learnt that the absolute value of 5 is 5. Therefore, the representation of the absolute value of the operation 2 + ( – 7 ) on the number line will be –

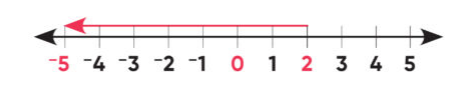
Absolute Value Equation

We have learnt above how to plot the absolute value of a number on a number line. Now, let us understand how we can derive the equation of the absolute value of a number. Let us consider the absolute values of 6 and – 6. We have learnt that –

| 6 | = 6 which is read as “ the absolute value of 6 is 6 “

| – 6 | = 6 which is read as “ the absolute value of – 6 is 6 “

From above, we can say that the number line is not just a way to show distance from zero; it’s also a useful way to graph equalities and inequalities that contain expressions with absolute value.

Now, let us consider the equation, | x | = 2

The variable x, in the equation above, will have two values, – 2 and 2

Both the values on a number can be represented as –

Now, we know that

| 2 | = 2 which is read as “ the absolute value of 2 is 2 “

| – 2 | = 2 which is read as “ the absolute value of – 2 is 2 “

This means that for | x | = 2, we will have,

| x | = x, for x > 0

| x | = – x, for x < 0

Using the conditions above, we can define the absolute value parent function. Let us now define the absolute value parent function.

Absolute Value Parent Function

The absolute value function f ( x ) is defined by

f ( x ) = | x | = {-x, x<0 0, x=0 x, x>0

is called an absolute value function. It is also called a modulus function. We observe that the domain of the absolute function is the set R of all real numbers and the range is the set of all non-negative real numbers. This means that,

R⁺ = { x ∈ R : x ≥ 0 }

Graph of Absolute Value Function

The graph of the absolute value function is shown in the below figure.

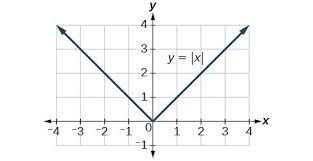
It is important to note here that for x > 0 the graph of the absolute value function coincides with the graph of the identity function, i.e. the line y = x and for x < 0 it is coincident to the line y = -x.

Properties of Absolute Value Function

The following are the properties of a modulus function –

For any real number x, we have, $\sqrt{x^2}$ = | x |

For example,

$\sqrt{cos^2x}$ = | cos x | = {coscos x, 0 ≤x ≤ $\frac{π}{2}$ -cos cos x , $\frac{π}{2}$<x<π

If a, b are positive real numbers, then,
1. x² ≤ a² ⬄| x | ≤ a ⬄ – a ≤ x ≤ a
2. x² ≤ a² ⬄| x | ≥ a ⬄ x ≥ a or ≤ x ≤ – a
3. x² < a² ⬄ | x | < a ⬄ – a < x < a
4. x² > a² ⬄ | x | > a ⬄ x < – a or x > a
For real numbers, x and y we have,
1. | x + y | = | x | + | y |, if ( x ≥ 0 and y ≥ 0 ) or ( x < 0 and y < 0 )
2. | x – y | = | x | – | y |, if ( x ≥ 0 and | x | ≥ | y | ) or ( x ≤ 0, y ≤ 0 and | x | ≥ | y | )
3. | x ± y | ≤ | x | + | y |
4. | x ± y | > | | x | – | y | |
Non-negativity If and b are real numbers, then | a | ≥ 0
Positive-definiteness If a is a real number, then, | a | = 0a = 0
Multiplicativity If and b are real numbers, then | a b | = | a| | b |
Subadditivity If and b are real numbers, then | a + b | ≤ | a | + | b |
Idempotence | | a | | = | a |
Symmetry | − a | = | a |
Identity of indiscernible If and b are real numbers, then | a – b | = 0 ⇔ a = b
Triangle inequality If and b are real numbers, then | a – b | ≤ | a – c | + | c – b |
Preservation of division If and b are real numbers, then | a / b |=| a | / | b | if b ≠ 0

Solved Examples

Example 1 Find the possible values of | 4 x | = 16

Solution We have been given the absolute function | 4 x | = 16 and we are required to find all its possible values.

We know that the value inside the absolute function can either be positive or be negative. This means that 4 x which is inside the absolute value function can either be positive or be negative. This means that we can write the given equation, | 4 x | = 16 as –

4 x = 16 or – 4 x =1 6

Let us solve both the equations we have obtained above individually.

We have,

4 x = 16

⇒ x = 164 = 4 ……………….. ( 1 )

Also,

– 4 x =1 6

⇒ x = $\frac{16}{-4}$ = – 4 ………….. ( 2 )

From equation ( 1 ) and equation ( 2 ), we can see that x can have both the values 4 as well as -4.

Hence, the possible values of | 4 x | = 16 will be x = 4 and x = – 4.

Example 2 Find the value of | 6 + 2 ( – 2 ) |

Solution We have been given the absolute value function | 6 + 2 ( – 2 ) | and we need to find its value.

We shall apply BODMAS rule to solve the expression we have been given inside the absolute value function. We have,

| 6 + 2 ( – 2 ) |

= | 6 – 4 |

= | 2 |

Now, we know that | 2 | = 2.

Therefore, the value of the | 6 + 2 ( – 2 ) | will be 2.

Example 3 Arrange the given numbers in ascending order.

– | – 1 4 | , | 1 2 | , | 7 | , | – 9 1 | , | – 5 | , | – 8 | , | – 6 5 | , | 6 |

Solution We have been given the following absolute values and we are required to arrange them in ascending order.

– | – 1 4 | , | 1 2 | , | 7 | , | – 9 1 | , | – 5 | , | – 8 | , | – 6 5 | , | 6 |

To arrange them in ascending order, we first need to find the absolute value of each number. Let us find the absolute values of the given numbers. We have,

– | – 1 4 | = – ( 1 4 ) = – 1 4

| 1 2 | = 1 2

| 7 | = 7

| – 9 1 | = 9 1

| – 5 | = 5

| – 8 | = 8

| – 6 5 | = 6 5

| 6 | = 6

The numbers we have obtained are – 1 4 , 1 2 , 7 , 9 1 , 5 , 8 , 6 5 and 6 .

Now, that we have obtained the absolute value of all numbers, let us arrange the results in ascending order. We will have,

– 1 4 , 5 , 6 , 7 , 8 , 1 2 , 6 5 , 9 1

After having sorted the results in ascending order, we will replace these numbers by their parent absolute value representations that we have been given in the question. We will then have,

– | – 1 4 | , | – 5 | , | 6 | , | 7 | , | 1 2 | , | – 6 5 | , | – 9 1 |

Therefore, the numbers – | – 1 4 | , | 1 2 | , | 7 | , | – 9 1 | , | – 5 | , | – 8 | , | – 6 5 | , | 6 |

When arranged in ascending order will be – | – 1 4 | , | – 5 | , | 6 | , | 7 | , | 1 2 | , | – 6 5 | , | – 9 1 |

Key Facts and Summary

The absolute value of a number refers to the distance of a number from the origin of a number line.
If the number is positive then it will result in a positive number only. And if the number is negative, then the modulus of this number will also be a positive number.
The symbol of absolute value is | x |, where x is an integer.
The number line is not just a way to show distance from zero; it’s also a useful way to graph equalities and inequalities that contain expressions with absolute value.
The function f ( x) is defined by
f ( x ) = | x | = {-x, x<0 x, x≥0
is called a modulus function. It is also called an absolute value function.
For any real number x, we have, $\sqrt{x^2}$ = | x |
If a, b are positive real numbers, then,
1. x² ≤ a² ⬄| x | ≤ a ⬄ – a ≤ x ≤ a
2. x² ≤ a² ⬄| x | ≥ a ⬄ x ≥ a or ≤ x ≤ – a
3. x² < a² ⬄ | x | < a ⬄ – a < x < a
4. x² > a² ⬄ | x | > a ⬄ x < – a or x > a
For real numbers, x and y we have,
1. | x + y | = | x | + | y |, if ( x ≥ 0 and y ≥ 0 ) or ( x < 0 and y < 0 )
2. | x – y | = | x | – | y |, if ( x ≥ 0 and | x | ≥ | y | ) or ( x ≤ 0, y ≤ 0 and | x | ≥ | y | )
3. | x ± y | ≤ | x | + | y |
4. | x ± y | > | | x | – | y | |
Non-negativity If and b are real numbers, then | a | ≥ 0
Positive-definiteness If a is a real number, then, | a | = 0a = 0
Multiplicativity If and b are real numbers, then | a b | = | a| | b |
Subadditivity If and b are real numbers, then | a + b | ≤ | a | + | b |
Idempotence | | a | | = | a |
Symmetry | − a | = | a |
Identity of indiscernible If and b are real numbers, then | a – b | = 0 ⇔ a = b
Triangle inequality If and b are real numbers, then | a – b | ≤ | a – c | + | c – b |
Preservation of division If and b are real numbers, then | a / b |=| a | / | b | if b ≠ 0

Recommended Worksheets

Finding the Absolute Value of Numbers Worksheets
Number Lines (Food Festival themed) Worksheets
One-Variable Equations (Employment Themed) Worksheets

Browse All Worksheets

We spend a lot of time researching and compiling the information on this site. If you find this useful in your research, please use the tool below to properly link to or reference Helping with Math as the source. We appreciate your support!