Number and Shape Patterns

Introduction

When we think of mathematics, the first thing that comes to our mind is numbers. We are aware of different kinds of numbers that have been defined such as natural numbers, whole numbers, decimals, fractions and so on. Each set of a number has its own unique characteristic that makes it a set. For instance, the set of even numbers comprises of all numbers that are divisible by 2. Similarly, prime numbers are the numbers that are not completely divisible by any other number other than themselves and the number 1. By seeing these examples can we say that the numbers can be put in a sort of a pattern? Let us find out.

Let us understand it through an example.

Observe the following pattern – 

Numbers and Primary Patterns

The number pattern tells the common relationship between the given set of numbers. In other words, a Number Pattern is the pattern or sequence in the given series of numbers. Let us now discuss some patterns that are formed by primary numbers.

Even and Odd Number Patterns

We are aware of natural numbers. Natural numbers are the numbers that begin from 1 and go on up to infinity. They are in the form of 1 , 2 , 3, 4 and so on. Natural numbers form two types of patterns, depending upon the fact whether they are odd or even. Recall that odd numbers are the numbers which when divided by 2 will leave 1 as a remainder. In other words, odd numbers are the numbers that are not divisible by 2. So, how is the pattern of odd numbers defined? The number pattern of odd numbers is defined by the numbers starting from 1 ,3 , 5 , 7 , 9  and so on. Mathematically, this pattern for natural numbers can also be represented as the following on a number line.

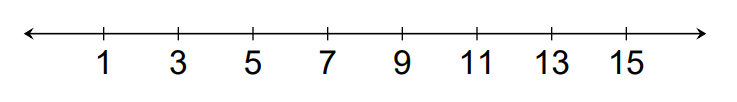
Therefore, the pattern of odd natural numbers is 1, 3, 5, 7, 9, 11 and so on. 

Similarly, let us recall what we mean by even numbers. Even numbers are the numbers which when divided by 2 will leave 0 as a remainder. In other words, even numbers are the numbers that are completely divisible by 2. So, how is the pattern of even numbers defined? The arithmetic pattern of even numbers is given by 2, 4, 6, 8, 10 and so on. Mathematically, this pattern for natural numbers can also be represented on a number line as  – 

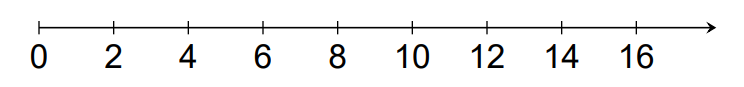
Therefore, the pattern of even natural numbers is 2, 4, 6, 8, 10, 12 and so on. 

Now, let us learn about patterns of some set of numbers.

Order of Number Patterns

Ordering is the general concept that is used to define number patterns. There are two ways in which the number patterns can be ordered – 

1. Ascending Order
2. Descending Order

Let us understand these in detail

Ascending Order of Number Patterns

Ascending order of number patterns is the pattern where the numbers are written from the smallest number to the largest number. For example, suppose we have a number pattern that contains all odd natural numbers from 2 to 10. The numbers in this pattern will be 3, 5, 7, 9. If this pattern is to be written from the smallest to the largest number, the pattern will be 3, 5, 7 and 9. This is known as a number pattern in ascending order.

Descending Order of Number Patterns

Descending order of number patterns is the pattern where the numbers are written from the largest number to the smallest number. For example, suppose we have a number pattern that contains all odd natural numbers from 2 to 10. The numbers in this pattern will be 3, 5, 7, 9. If this pattern is to be written from the largest number to the smallest number, the pattern will be 9, 7, 5 and 3. This is known as a number pattern in descending order.

Types of Number and Shape Patterns Based on their Order

In the example above, we have seen that addition can be used to generate an arithmetic pattern. Is this the only way to generate a number or a shape pattern? Following are the different types of number and shape patterns that are most commonly in use – 

Growing Pattern

As the name suggests, the growing pattern is the pattern where the numbers or shapes are present in an increasing order.  Let us understand it using an example.

We can see in the shape pattern above, the first term consists of 1 star. The second term consists of 2 stars. The third term consists of 3 stars. Hence we can see that there is an increasing pattern in the number of stars in the given pattern. What would be the fourth term of the pattern? We can see that every term gets increased by 1. Since the third term of the pattern has 3 stars, this means that the fourth term of the shape pattern will be four stars. It will be represented as – 

Reducing Pattern 

Again, as the name signifies, a reducing pattern is the arithmetic pattern in which the numbers are present in the decreasing order.   Let us understand it through an example.

We can see in the shape pattern above, the first term consists of 5 capital alphabets A. The second term consists of 4 capital alphabets A. The third term consists of 3 capital alphabets A. The fourth term consists of 2 capital alphabets A. Hence we can see that there is a decreasing pattern in the number of capital alphabet A in the given pattern. What would be the fifth term of the pattern? We can see that every term gets decreased by 1. Since the fourth term of the pattern has 2 capital alphabets of A, this means that the fifth term of the shape pattern will be 1 capital alphabet A. It will be represented as – 

Recurring Pattern 

In the recurring pattern of numbers, the same sets of numbers keep repeating themselves to form a pattern of numbers. Let us understand it through an example.

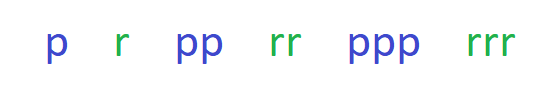
We can see in the shape pattern above, the first term consists of a single alphabet p. The second term consists of a single alphabet r. Now, the third term consists of two alphabet pp. the fourth term consists of two alphabets rr. This means that in this pattern there is a repetition of the alphabets p and r term by term along with an increment by 1 from the previous tern. Hence this pattern is a recurring pattern. The next two terms of this pattern will be 

Types of number Patterns

There are different number patterns that are commonly used for various mathematical operations. Let us discuss some of the common number patterns.

Arithmetic Number Pattern

As the name suggests, this pattern is formed by using the basic arithmetic operations between the numbers. Recall that there are four basic arithmetic operators, namely, addition, subtraction, multiplication and division. This means that a number pattern can be formed by either adding or subtracting a common digit to the previous term to obtain the next term of the pattern.

Let us understand this by an example.

Suppose we have a number, say 2.

We add 3 to this number. We have, 2 + 3 = 5

Now, we again add 3 to the result that we obtained in the previous step. We will have, 5 + 3 = 8.

Similarly, we again add 3 to the result that we obtained in the previous step. We will have, 8 + 3 = 11

Hence, we can see that a pattern is formed by the numbers as 2, 5, 8, 11 and so on.

Triangular Number Pattern

Triangular numbers are generated from a pattern of dots that form a triangle. In other words, the triangular number sequence is the representation of the numbers in the form of an equilateral triangle. The pattern formed by the triangular numbers is such that the sum of the previous number and the order of the succeeding number results in the sequence of triangular numbers. In other words, the number of the pattern of dots that form a triangle will give a triangular number sequence. This arrangement is represented as below –

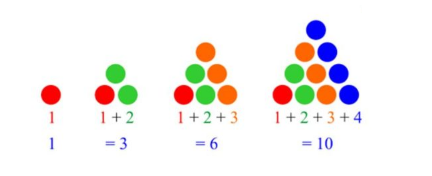
Number Pattern of Square Numbers

Square numbers are the numbers obtained when a number is multiplied by itself. For instance 2 x 2 = 4, therefore, 4 is the square of 2. Similarly, 3 x 3 = 9, therefore, 9 is the square of 3. The pattern of square numbers is given by 1, 4, 9, 16, 25, 36 and so on. In other words, a square number pattern is a sequence in which the numbers are forming the pattern in the form of a square.

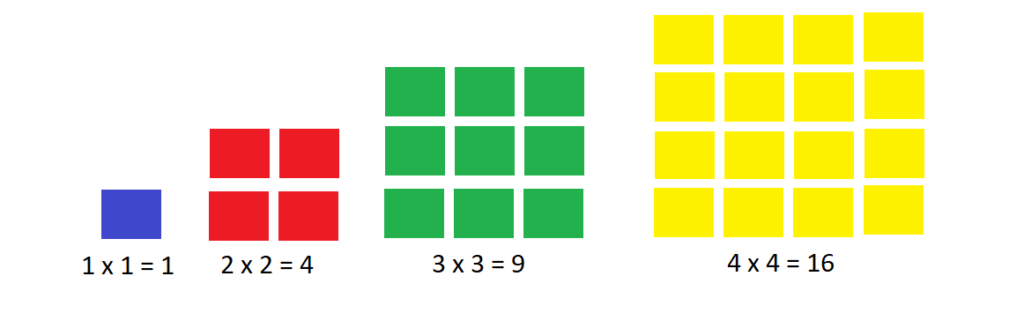
The number pattern of square numbers is formed as follows – 

1 ² = 1 x 1 = 1

2 ² = 2 x 2 = 4

3 ² = 3 x 3 = 9

4 ² = 4 x 4 = 16

5 ² = 5 x 5 = 25

Number Pattern of Cube Numbers

Cube numbers are the numbers obtained when a number is multiplied twice with itself. For instance 2 x 2 x 2 = 8, therefore, 8 is the cube of 2. Similarly, 3 x 3 x 3 = 27, therefore, 27 is the cube of 3. The number pattern of cube numbers is given by 1, 8, 27, 12, 64, 125 and so on. In other words, the cube number pattern is the sequence of numbers, which form the pattern in the form of the cube. A cube is a three-dimensional figure.

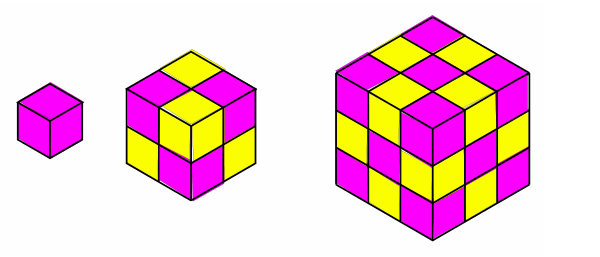
The number pattern of cube numbers is formed as follows – 

1 ³ = 1 x 1 x 1 = 1

2 ³ = 2 x 2 x 2 = 8

3 ³ = 3 x 3 x 3 = 27

4 ³ = 4 x 4 x 4 = 64

5 ³ = 5 x 5 x 5 = 125

Common Characteristics of Number and Shape Patterns

The following are the common characteristics of number and shape patterns – 

1. The number patterns could be ascending, descending, multiples of a certain number, or series of even numbers, odd numbers, etc.
2. Patterns can be of shapes, objects, and colours as well and not just numbers. 
3. In an arithmetic sequence, each successive term is obtained by adding the common difference to its preceding term.

Solved Examples

Example 1 What will be the 16^th shape in the following pattern ? 

Solution We have been given a shape pattern. We need to find the 16 term of this shape pattern.

Observe the shape pattern carefully.

To help answer the question, we can number the shapes in the pattern. There are 10 shapes shown in the pattern. 

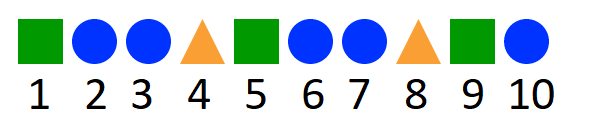
We need to work out what the 16th shape would be? First, we need to find the rule for the pattern. The pattern is given by – square, circle, circle, triangle, square, circle, circle, triangle. There are four shapes in the pattern. We can see that it is a repeated pattern with the repetitions being in the order: square, circle, circle, and triangle.

To help us find the 16th shape, we can count in fours until we reach 16. This means that shapes number four, eight, 12, and 16 would be an orange triangle. 

So the 16th shape in this pattern would be the orange triangle.

Example 2 We have been given a repeating shape pattern of the following order. 

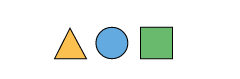
What will be the first 9 terms of this pattern?

Solution Observe the pattern carefully. The first shape is a triangle. The second shape is a circle and the third shape is a square. We have also been given that the pattern is a repeating pattern. This means that these 3 shapes will repeat themselves in the same order. Therefore, the first 9 terms of this shape will be – 

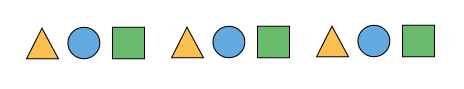
Example 3 Find the eighth term of the following number pattern –

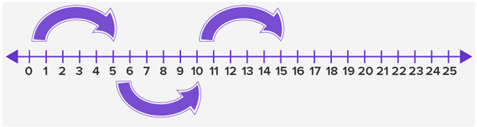
Solution We have been given a number pattern and we need to find the eighth number of that pattern. Let us first understand how the number pattern has been formed.

We can see that the first number of the given number pattern is 0 ……… ( 1)

Now, the first arrow of the pattern points to the number 5. Therefore, the second number of the pattern is 5.

Can we see a relation between the first term and the second term?

Let us check their difference, we have 5 – 0 = 5 ……………………… ( 2 )

Now, the second arrow of the pattern points to the number 10. Therefore, the second number of the pattern is 10.

Can we see a relation between the second term and the third term?

Let us check their difference, we have 10 – 5 = 5 ……………………… ( 3 )

Again, the third arrow of the pattern points to the number 15. Therefore, the third number of the pattern is 15.

Can we see a relation between the third term and the fourth term?

Let us check their difference, we have 15 – 10 = 5 ……………………… ( 4 )

From ( 1 ), ( 2 ), ( 3 ), and ( 4 ), we can see that the difference in any two terms in the pattern = 5. This means that the given number pattern has been formed by adding 5 to the previous number to obtain the next number. We must therefore, obtain more number of the series as  –

First Number = 0

Second Number = 0 + 5 = 5

Third Number = 5 + 5 = 10

Fourth Number = 10 + 5 =15

Fifth Number = 15 + 5 = 20

Sixth Number = 20 + 5 = 25

Seventh Number = 25 + 5 = 30

Eighth Number = 30 + 5 =35

Hence, the eighth number in the given number pattern will be 35.

Key Facts and Summary

1. Number Pattern is the pattern or sequence in the given series of numbers.
2. Odd numbers are the numbers which when divided by 2 will leave 1 as a remainder. The number pattern of odd numbers is defined by the numbers starting from 1 ,3 , 5 , 7 , 9  and so on.
3. Even numbers are the numbers which when divided by 2 will leave 0 as a remainder. The number pattern of even natural numbers is defined by the numbers starting from 2, 4, 6, 8, 10, 12 and so on. 
4. Ascending order of number patterns is the pattern where the numbers are written from the smallest number to the largest number.
5. Descending order of number patterns is the pattern where the numbers are written from the largest number to the smallest number.
6. The growing pattern is the pattern where the numbers or shapes are present in an increasing order.
7. A reducing pattern is the arithmetic pattern in which the numbers are present in the decreasing order.   
8. In the recurring pattern of numbers, the same sets of numbers keep repeating themselves to form a pattern of numbers.