Conjugate Complex Numbers

Introduction

If a and b are natural numbers such that a > b, then the equation x + a = b is not solvable in N, the set of natural numbers.  This means that there is no natural number satisfying the equation x + a = b. so, the set of natural numbers is extended to form the set I of integers in which every equation of the form x + a = b, for a and b being natural numbers is solvable. However, the equations of the form x a = b, where a ≠ 0 and a and b being integers are not solvable for I also. Hence, the set I of integers is extended to obtain the set Q of all rational numbers in which every equation of the form x a  = b, where a ≠ 0 and a and b being integers is solvable. But, the equations of the form x ² = 2, x ² = 3 etc. are not solvable in Q because there is no rational number whose square is 2. Such numbers are known as irrational numbers. The set Q of all rational numbers is extended to obtain the set of R of real numbers that include both rational and irrational numbers. However, the equations of the form x ² + 1 = 0, x ² + 4 = 0, etc. are not solvable in R which means that there is no real number whose square is a negative real number. Euler was the first mathematician to introduce the symbol i ( iota ) for the square of – 1, i.e. a solution of x ² + 1 = 0 with the property i 2 = – 1. He also called this symbol as the imaginary unit. This gave the concept of complex numbers Let us learn more about them. 

Definition

The complex conjugate of a complex number, z, is its mirror image with respect to the horizontal axis ( or x – axis ). In other words, a complex conjugate of a complex number is another complex number whose real part is the same as the original complex number and the magnitude of the imaginary part is the same with the opposite sign. This is similar to the definition of a conjugate we learn in mathematics in general. A conjugate in Mathematics is formed by changing the sign of one of the terms in a binomial. For example, if the binomial number is a + b, the conjugate of this number will be formed by changing the sign of either of the terms. If we change the sign of b, the conjugate formed will be a – b. Therefore, in mathematics, a + b and a – b are both conjugates of each other.

How do we write Conjugate of a Complex Number?

Let z =  a + i b be a complex number. Then the conjugate of z is defined by $\overline{z}$ and is equal to a – i b. 

Thus, if z =  a + i b ⇒ $\overline{z}$ = a – i b

Therefore, it follows from the definition that the conjugate of a complex number is obtained by replacing i by – i .  

Let us understand it through an example.

Suppose we have a complex number z = 3 + 4 i. What would be the conjugate of this complex number?

The conjugate of the complex number z = 3 + 4 I would be z = 3 – 4 i

Properties of Conjugate of Complex Numbers

The following are the properties of the conjugate of a complex number – 

If z ₁, z ₂, and z ₃ are three complex numbers and let z  = a + i b, z ₁  = a ₁ + i b ₁ and z ₂ = a ₂ + i b ₂ Then, 

1. The conjugate of a conjugate of a complex number is the complex number itself, i.e. ( z̿ ) = z. this can be proved as $\overline{z}$  = a + i b implies that z  = a – i b. This further means that ( z̿ ) =  $\overline{a – i b}$ = a + i b. Hence, we can say that ( z̿ ) = z
2. The sum of a complex number and its complex conjugate is equal to twice the real part of the complex number, i.e. z + $\overline{z}$ = 2 Re ( z ) . This can be proved as – z + $\overline{z}$ = a + i b + a – i b = 2 a = 2 Re ( z )
3. The difference between a complex number and its complex conjugate is equal to twice the imaginary part of the complex number, i.e. z – $\overline{z}$ = 2 i Im ( z ). This can be proved as -z – $\overline{z}$ = a + i b – ( a – i b ) =  a + i b –  a + i b  = 2 i b = 2 i Im ( z )
4. If z =  $\overline{z}$, this implies that z is purely real. The vice versa of this statement also holds true, i.e. if – $\overline{z}$ = z, this implies that z is purely real.
5. If z +  $\overline{z}$ = 0, this implies that z is purely imaginary. 
6. The complex conjugate of the sum of two complex numbers is equal to the sum of the complex conjugates of the two complex numbers, i.e. $\overline{z_1+ z_2}$ = $\overline{z_1 + z_2}$
7. The complex conjugate of the product of two complex numbers is equal to the product of the complex conjugates of the two complex numbers, i.e. $\overline{z_1.  z_2}$ = $\overline{z_1 .  z_2}$
8. The complex conjugate of the quotient of two complex numbers is equal to the quotient of the complex conjugates of the two complex numbers, i.e. $\frac{\overline{z_1}}{\overline{z_2}}$ = $\frac{\overline{z_1}}{\overline{z_2}}$
9. If z = a + i b , then z . $\overline{z}$ = a ^{2 +} b ²  = ⌊z²⌋

Argand Diagram of a Conjugate of a Complex Number 

Let us recall what we mean by an argand diagram of a complex number. A complex number z = x + i y can be represented by a point ( x, y ) on the plane which is known as the Argand plane. To represent z = x + i y in geometric form, we take mutually perpendicular straight lines. Now we will plot a point whose x and y coordinates are represented by the real and the imaginary parts of z. This point P ( x, y ) represents the complex number  z = x + i y. Below is the geometric representation of the point P ( x, y ) on the complex plane.

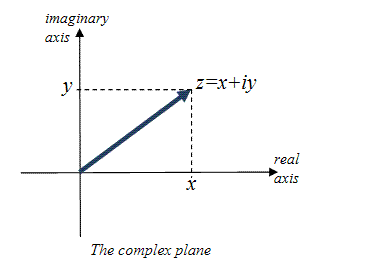
Some important points to remember here are – 

1. If the complex number is purely real, then its imaginary part will be 0. This means that a purely real number will be represented by a point on the x – axis. This is why x – axis is known as the real axis.
2. If the complex number is purely imaginary, then its real part will be 0. This means that a purely imaginary number will be represented by a point on the y – axis. This is why y – axis is known as the imaginary axis.
3. If P ( x, y ) is a point on the complex plane, then the point P ( x, y )  represents a complex number z = x + i y. the complex number z = x + i y is known as the affix of the point P.
4. The plane in which we represent a complex number in geometrical form is known as the complex plane or Argand plane or the Gaussian plane. The point P plotted on the Argand plane is called the Argand diagram.

Argument or Amplitude of a Complex number for different signs of real and imaginary parts

Let us now discuss the Argument or Amplitude of a Complex number for different signs of real and imaginary parts. There can be four different conditions depending upon the signs of real and imaginary parts. These four conditions are – 

1. Argument of z = x + i y when x > 0 and y > 0
2. Argument of z = x + i y when x < 0 and y > 0
3. Argument of z = x + i y when x < 0 and y < 0
4. Argument of z = x + i y when x > 0 and y < 0

Let us discuss these one by one

Argument of z = x + i y when x > 0 and y > 0

Since x and y are both positive, therefore, the point P ( x, y ) representing z = x + i y in the Argand plane lies in the first quadrant. Let  be the argument of z and let θ be the acute angle satisfying tan = | y / x | . Below is the geometrical representation of this case – 

Argument of z = x + i y when x < 0 and y > 0

Since x is less than zero, which means it is negative and y is positive, therefore, the point P ( x, y ) representing z = x + i y in the Argand plane lies in the second quadrant. Let  be the argument of z and let be the acute angle satisfying tan = | y / x | . Below is the geometrical representation of this case – 

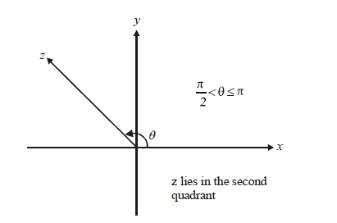
Argument of z = x + i y when x < 0 and y < 0

Since x and y are both negative, therefore, the point P ( x, y ) representing z = x + i y in the Argand plane lies in the third quadrant. Let  be the argument of z and let be the acute angle satisfying tan = | y / x | . Below is the geometrical representation of this case – 

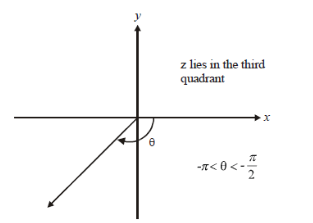
Argument of z = x + i y when x > 0 and y < 0

Since y is less than zero, which means it is negative and x is positive, therefore, the point P ( x, y ) representing z = x + i y in the Argand plane lies in the fourth quadrant. Let  be the argument of z and let be the acute angle satisfying tan = | y / x | . Below is the geometrical representation of this case – 

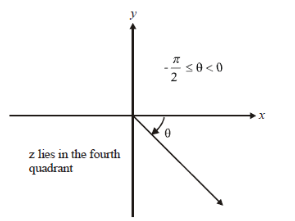
From the above, we can define an algorithm for finding the argument of a complex number using the complex plane.

Now, the argand diagram of the conjugate of a complex number will be – 

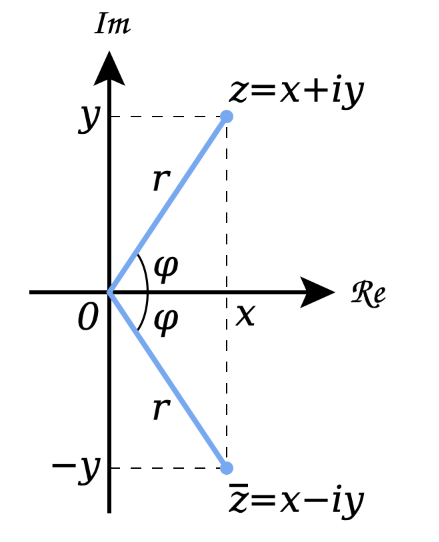
The length of line joining the number is its absolute value also known as modulus and the angle, this line makes with positive side of real axis or x – axis is known as argument of the number.

Multiplication of Complex Conjugate

Let us consider two complex numbers, say, z₁ = ( a + i b ) and z₂ = ( c + i d ). Let us how we can multiply these two complex numbers. 

Since we need to multiply z₁ and z₂, we will have,

z₁ x z₂ = ( a + i b ) ( c + i d ) . . . . . . . . . . . . . . . . . . . . . . . . . ( 1 ) 

⇒ z₁ x z₂ = a c + i ( a d ) + i ( b c ) +  i ² ( b d )

We know that i ² = – 1 , therefore, substituting the value of i ² in the above equation, we will have,

z₁ x z₂ = a c + i ( a d ) + i ( b c ) +  ( – 1 ) ( b d )

Now, we will combine the real numbers with the imaginary numbers, we will get,

z₁ x z₂ = ( a c  – b d ) + i ( a d +  b c ) . . . . . . . . . . . . . . . . ( 2 )

So, we can say that for any two complex numbers, z₁ = ( a + i b ) and z₂ = ( c + i d ), z₁ x z₂ = ( a c  – b d ) + i ( a d +  b c )

Now, when a complex number is multiplied by its complex conjugate, the product is a real number whose value is equal to the square of the magnitude of the complex number.

Now, (a + i b )( a – i b ) = a ² – ( i b ) ² = a ² – i ² b ² = a ² + b ² 

Key Facts and Summary

1. The complex conjugate of a complex number, z, is its mirror image with respect to the horizontal axis ( or x – axis ).
2. The conjugate of a conjugate of a complex number is the complex number itself, i.e. ( z̿ ) = z. this can be proved as $\overline{z}$  = a + i b implies that z  = a – i b. This further means that ( z̿ ) =  $\overline{a – i b}$ = a + i b. Hence, we can say that ( z̿ ) = z
3. The sum of a complex number and its complex conjugate is equal to twice the real part of the complex number, i.e. z + $\overline{z}$ = 2 Re ( z ) . This can be proved as – z + $\overline{z}$ = a + i b + a – i b = 2 a = 2 Re ( z )
4. The difference between a complex number and its complex conjugate is equal to twice the imaginary part of the complex number, i.e. z – $\overline{z}$ = 2 i Im ( z ). This can be proved as -z – $\overline{z}$ = a + i b – ( a – i b ) =  a + i b –  a + i b  = 2 i b = 2 i Im ( z )
5. If z =  $\overline{z}$, this implies that z is purely real. The vice versa of this statement also holds true, i.e. if – $\overline{z}$ = z, this implies that z is purely real.
6. If z +  $\overline{z}$ = 0, this implies that z is purely imaginary. 
7. The complex conjugate of the sum of two complex numbers is equal to the sum of the complex conjugates of the two complex numbers, i.e. $\overline{z_1+ z_2}$ = $\overline{z_1 + z_2}$
8. The complex conjugate of the product of two complex numbers is equal to the product of the complex conjugates of the two complex numbers, i.e. $\overline{z_1.  z_2}$ = $\overline{z_1 .  z_2}$
9. The complex conjugate of the quotient of two complex numbers is equal to the quotient of the complex conjugates of the two complex numbers, i.e. $\frac{\overline{z_1}}{\overline{z_2}}$ = $\frac{\overline{z_1}}{\overline{z_2}}$
10. If z = a + i b , then z . $\overline{z}$ = a ^{2 +} b ²  = ⌊z²⌋
11. If z = a + i b is called a complex number, then “ a “ is called the real part of z and “ b “ is known as the imaginary part of z. the real part of z is denoted by Re ( z ) and the imaginary part of z is denoted by Im ( z ).
12. The modulus of a complex number z = a + i b is denoted by | z | and is defined as 
    | z |  = $\sqrt{a^2+ b^2} = \sqrt{{ Re ( z ) }^2+ Im ( z )^2}$
13. The complex plane (also known as the Gauss plane or Argand plane) is a geometric method of depicting complex numbers in a complex projective plane.
14. A complex number z = x + i y can be represented by a point ( x, y ) on the plane which is known as the Argand plane.
15. If the complex number is purely real, then its imaginary part will be 0. This means that a purely real number will be represented by a point on the x – axis. This is why x – axis is known as the real axis.
16. If the complex number is purely imaginary, then its real part will be 0. This means that a purely imaginary number will be represented by a point on the y – axis. This is why y – axis is known as the imaginary axis.

Recommended Worksheets

Complex Fractions (Fashion Themed) Worksheets
Natural Numbers (Arbor Day Themed) Math Worksheets
Subtracting Whole Numbers and Decimals (Tenths to Thousandths) 5th Grade Math Worksheets