Number Names

Introduction

When we think of mathematics, the first thing that comes to our mind is numbers. We are already familiar with the counting of numbers, 1, 2, 3, 4, 5, 6 and so on. There are different ways in which these numbers can be represented, be it in the form of numerals or writing them in word form. What do we call the numbers when we use alphabets to represent them? This is where we find the use of the term, “ number names “. What are numbers names and what are the rules to write them? Let us find out.

Definition

Number names are a way in which we can represent numbers in word form. In other words, number names are a way in which numbers are written in words using the English alphabet.

What are Number Names?

For example, we can use the word “ one “ to represent the number “ 1 “, we can use the word “ two “ to represent the number “ 2 “  and so on. In this way, we can represent any number in word form which is known as the number name for the number. Before we move to understand how to write various numbers, it is important to recall what we mean by place value of numbers.

Number Names from 1 to 100

The below table contains numbers names from 1 to 100 in English words – 

Number	Number Name	Number	Number Name
1	One	5 1	Fifty – one
2	Two	5 2	Fifty – two
3	Three	5 3	Fifty – three
4	Four	5 4	Fifty – four
5	Five	5 5	Fifty – five
6	Six	5 6	Fifty – six
7	Seven	5 7	Fifty – seven
8	Eight	5 8	Fifty – eight
9	Nine	5 9	Fifty – nine
1 0	Ten	6 0	Sixty
1 1	Eleven	6 1	Sixty – one
1 2	Twelve	6 2	Sixty – two
1 3	Thirteen	6 3	Sixty – three
1 4	Fourteen	6 4	Sixty – four
1 5	Fifteen	6 5	Sixty – five
1 6	Sixteen	6 6	Sixty – six
1 7	Seventeen	6 7	Sixty – seven
1 8	Eighteen	6 8	Sixty – eight
1 9	Nineteen	6 9	Sixty – nine
2 0	Twenty	7 0	Seventy
2 1	Twenty – one	7 1	Seventy – one
2 2	Twenty – two	7 2	Seventy – two
2 3	Twenty – three	7 3	Seventy – three
2 4	Twenty – four	7 4	Seventy – four
2 5	Twenty – five	7 5	Seventy – five
2 6	Twenty – six	7 6	Seventy – six
2 7	Twenty – seven	7 7	Seventy – seven
2 8	Twenty – eight	7 8	Seventy – eight
2 9	Twenty – nine	7 9	Seventy – nine
3 0	Thirty	8 0	Eighty
3 1	Thirty – one	8 1	Eighty – one
3 2	Thirty – two	8 2	Eighty – two
3 3	Thirty – three	8 3	Eighty – three
3 4	Thirty – four	8 4	Eighty – four
3 5	Thirty – five	8 5	Eighty – five
3 6	Thirty – six	8 6	Eighty – six
3 7	Thirty – seven	8 7	Eighty – seven
3 8	Thirty – eight	8 8	Eighty – eight
3 9	Thirty – nine	8 9	Eighty – nine
4 0	Forty	9 0	Ninety
4 1	Forty – one	9 1	Ninety – One
4 2	Forty – two	9 2	Ninety – two
4 3	Forty – three	9 3	Ninety – three
4 4	Forty – four	9 4	Ninety – four
4 5	Forty – five	9 5	Ninety – five
4 6	Forty – six	9 6	Ninety – six
4 7	Forty – seven	9 7	Ninety – seven
4 8	Forty – eight	9 8	Ninety – eight
4 9	Forty – nine	9 9	Ninety – nine
5 0	Fifty	1 0 0	Hundred

Number Names in International System

Number names in the international system are written in accordance with the internal place value system. Place value is the basis of our entire number system. This is the system in which the position of a digit in a number determines its value. The place value of a digit in a number is the value it holds to be at the place in the number. Therefore, the number 65,471 is different from 17,645 because the digits are in different positions. 

Place Value Chart of Numbers

Let us now recall what we mean by a Place Value Chart? A place-value chart is a way to make sure digits are in the correct places.  The place value chart of numbers is followed by most of the countries around the world. In this system, a number is split up into groups or periods. The place value chart of numbers is thus represented as  – 

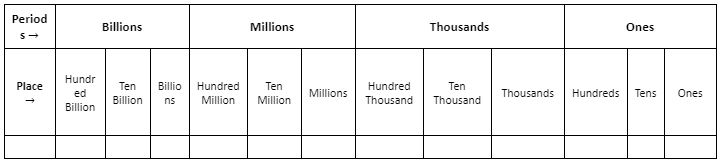
From the place value system, we can say that

1 Million =  1000 thousand
1 Billion =  1000 Million

Let us now write the number names from 101 to 1000 in accordance with the place value system.

Number Names from 101 to 1000

The following table contains numbers names from 101 to 1000 in English words – 

Number	Number Name
1 0 1	One hundred one
1 0 2	One hundred two
1 0 3	One hundred Three
1 0 4	One hundred Four
1 0 5	One hundred Five
1 0 6	One hundred Six
1 0 7	One hundred Seven
1 0 8	One hundred Eight
1 0 9	One hundred Nine
1 1 0	One hundred ten
1 2 0	One hundred twenty
1 3 0	One hundred thirty
1 4 0	One hundred forty
1 5 0	One hundred fifty
1 6 0	One hundred sixty
1 7 0	One hundred seventy
1 8 0	One hundred eighty
1 9 0	One hundred ninety
2 0 0	Two hundred
2 5 0	Two hundred
3 0 0	Three hundred
3 5 0	Three hundred
4 0 0	Four hundred
4 5 0	Four hundred
5 0 0	Five hundred
5 5 0	Five hundred
6 0 0	Six hundred
6 5 0	Six hundred
7 0 0	Seven hundred
7 5 0	Seven hundred
8 0 0	Eight hundred
8 5 0	Eight hundred
9 0 0	Nine hundred
9 5 0	Nine hundred
1 0 0 0	One thousand

Now that we have learnt how to write number names of various numbers, can we define certain rules that can help us write eh number name for any number? Let us find out.

Rule for writing Number Names

The following are the rules that need to be considered while writing number names corresponding to any number  –

1. The numbers from 1 to 9 are called ones according to the place value system. The place value these numbers is written in words as, one, two, three, four, five, six, seven, eight and nine.
2. The least number which is at tens place is 10, which in the form of number names is written as ten.
3. The numbers from 11 to 19 are written in number names as, eleven, twelve, thirteen, fourteen, fifteen, sixteen, seventeen, eighteen and nineteen. It is important to note here that the next number after nineteen ( 19 ) is 20, which in the form of number name is written as twenty.
4. After twenty, the numbers follow the pattern in such a way that they are written in words as thirty, forty, fifty, sixty, seventy, eighty, ninety and so on.
5. The preceding numbers are linked with these words and mentioned from one to nine. For example, twenty-one, twenty-two, etc.

Number Names in Indian System

We know that in the Indian numeration system, the number names start ones, tens, hundreds, thousands, lakhs, ten-lakhs, one crore, ten-crore and so on. Below are examples of the number names as written according to the Indian numeration system – 

Number Name of 4000 – Four thousand

Number Name of 7000 – Seven thousand

Number Name of 10000 – Ten Thousand

Number Name of 15000 – Fifteen Thousand

Number Name of 16000  – Sixteen Thousand

Number Name of 19000 –  Nineteen thousand

Similarly, we will have, 

Number Name of 20,000 – Twenty Thousand

Number Name of 25,000 – Twenty Five Thousand

Number Name of 30,000 – Thirty Thousand

Number Name of 35,000 – Thirty-Five Thousand

Number Name of 40, 000 – Forty Thousand

Number Name of 45,000 – Forty – Five Thousand

Number Name of 50,000 – Fifty Thousand

Number Name of 55,000 – Fifty – Five Thousand

Number Name of 60,000 – Sixty Thousand

For larger numbers, we will have, 

100,000 – One Lakh 

200, 000 – Two Lakhs 

300, 000 – Three Lakhs 

400, 000 – Four Lakhs 

500, 000 – Five Lakhs 

600, 000 – Six Lakhs 

700, 000 – Seven Lakhs 

800, 000 – Eight Lakhs 

900, 000 – Nine Lakhs 

10,00,000 – Ten Lakhs

1,00,00,000 – One Crore

Number Names for Ordinal Numbers

We know that ordinal numbers are the numbers that talk about the position of objects. The numbers 1^st, 2^nd, 3^rd and so on are examples of ordinal numbers. Below table indicates the number names of ordinal numbers from 1 to 100 – 

Number	Ordinal Number	Ordinal Number Name	Number	Ordinal Number	Ordinal Number Name
1	1 s t	First	5 1	5 1 s t	Fifty – First
2	2 n d	Second	5 2	5 2 n d	Fifty – Second
3	3 r d	Third	5 3	5 3 r d	Fifty – Third
4	4 t h	Fourth	5 4	5 4 t h	Fifty – Fourth
5	5 t h	Fifth	5 5	5 5 t h	Fifty – Fifth
6	6 t h	Sixth	5 6	5 6 t h	Fifty – Sixth
7	7 t h	Seventh	5 7	5 7 t h	Fifty – Seventh
8	8 t h	Eighth	5 8	5 8 t h	Fifty – Eighth
9	9 t h	Ninth	5 9	5 9 t h	Fifty – Ninth
1 0	1 0 t h	Tenth	6 0	6 0 t h	Sixtieth
1 1	1 1 t h	Eleventh	6 1	6 1 s t	Sixty – First
1 2	1 2 t h	Twelfth	6 2	6 2 n d	Sixty – Second
1 3	1 3 t h	Thirteenth	6 3	6 3 r d	Sixty – Third
1 4	1 4 t h	Fourteenth	6 4	6 4  t h	Sixty – Fourth
1 5	1 5 t h	Fifteenth	6 5	6 5 t h	Sixty – Fifth
1 6	1 6 t h	Sixteenth	6 6	6 6 t h	Sixty – Sixth
1 7	1 7 t h	Seventeenth	6 7	6 7 t h	Sixty – Seventh
1 8	1 8 t h	Eighteenth	6 8	6 8 t h	Sixty – Eighth
1 9	1 9 t h	Nineteenth	6 9	6 9 t h	Sixty – Ninth
2 0	2 0 t h	Twentieth	7 0	7 0 t h	Seventieth
2 1	2 1 s t	Twenty – First	7 1	7 1 s t	Seventy – First
2 2	2 2 n d	Twenty – Second	7 2	7 2 n d	Seventy – Second
2 3	2 3 r d	Twenty – Third	7 3	7 3 r d	Seventy – Third
2 4	2 4  t h	Twenty – Fourth	7 4	7 4 t h	Seventy – Fourth
2 5	2 5 t h	Twenty – Fifth	7 5	7 5 t h	Seventy – Fifth
2 6	2 6 t h	Twenty – Sixth	7 6	7 6 t h	Seventy – Sixth
2 7	2 7 t h	Twenty – Seventh	7 7	7 7 t h	Seventy – Seventh
2 8	2 8 t h	Twenty – Eighth	7 8	7 8 t h	Seventy – Eighth
2 9	2 9 t h	Twenty – Ninth	7 9	7 9 t h	Seventy – Ninth
3 0	3 0 t h	Twenty – Tenth	8 0	8 0 t h	Eightieth
3 1	3 1 s t	Thirty – First	8 1	8 1 s t	Eighty – First
3 2	3 2 n d	Thirty – Second	8 2	8 2 n d	Eighty – Second
3 3	3 3 r d	Thirty – Third	8 3	8 3 r d	Eighty – Third
3 4	3 4 t h	Thirty – Fourth	8 4	8 4 t h	Eighty – Fourth
3 5	3 5 t h	Thirty – Fifth	8 5	8 5 t h	Eighty – Fifth
3 6	3 6 t h	Thirty – Sixth	8 6	8 6 t h	Eighty – Sixth
3 7	3 7 t h	Thirty – Seventh	8 7	8 7 t h	Eighty – Seventh
3 8	3 8 t h	Thirty – Eighth	8 8	8 8 t h	Eighty – Eighth
3 9	3 9 t h	Thirty – Ninth	8 9	8 9 t h	Eighty – Ninth
4 0	4 0 t h	Fortieth	9 0	9 0 t h	Ninetieth
4 1	4 1 s t	Forty – First	9 1	9 1 s t	Ninety – First
4 2	4 2 n d	Forty – Second	9 2	9 2 n d	Ninety – Second
4 3	4 3 3 d	Forty – Third	9 3	9 3 r d	Ninety – Third
4 4	4 4  t h	Forty – Fourth	9 4	9 4 t h	Ninety – Fourth
4 5	4 5 t h	Forty – Fifth	9 5	9 5 t h	Ninety – Fifth
4 6	4 6 t h	Forty – Sixth	9 6	9 6 t h	Ninety – Sixth
4 7	4 7 t h	Forty – Seventh	9 7	9 7 t h	Ninety – Seventh
4 8	4 8 t h	Forty – Eighth	9 8	9 8 t h	Ninety – Eighth
4 9	4 9 t h	Forty – Ninth	9 9	9 9 t h	Ninety – Ninth
5 0	5 0 t h	Fiftieth	1 0 0	1 0 0 t h	Hundredth

Key Facts and Summary

1. Number names a way in which we can represent numbers in word form.
2. Place value is the basis of our entire number system. This is the system in which the position of a digit in a number determines its value. The place value of a digit in a number is the value it holds to be at the place in the number.
3. The numbers from 1 to 9 are called ones according to the place value system. The place value these numbers is written in words as, one, two, three, four, five, six, seven, eight and nine.
4. The least number which is at tens place is 10, which in the form of number names is written as ten.
5. The numbers from 11 to 19 are written in number names as, eleven, twelve, thirteen, fourteen, fifteen, sixteen, seventeen, eighteen and nineteen. It is important to note here that the next number after nineteen ( 19 ) is 20, which in the form of number name is written as twenty.
6. After twenty, the numbers follow the pattern in such a way that they are written in words as thirty, forty, fifty, sixty, seventy, eighty, ninety and so on.
7. The preceding numbers are linked with these words and mentioned from one to nine. For example, twenty-one, twenty-two, etc.
8. Ordinal numbers are the numbers that talk about the position of objects. The numbers 1^st, 2^nd, 3^rd and so on are examples of ordinal numbers.

Recommended Worksheets

Place Value (International Children’s Day Themed) Math Worksheets
Ordinal Numbers (Children’s Day Themed) Math Worksheets
Place Value of a 3-digit Number 2nd Grade Math Worksheets