Definition
A circle is defined as the locus of a point that moves in a plane such that its distance from a fixed point in that plane is always constant. The fixed point is called the centre of the circle and the constant distance is called the radius of the circle.
Parts of a Circle
Circumference – The circumference of a circle is the distance around the boundary of the circle. In other words, it is the perimeter of the circle.
Radius – Radius is the distance from the centre of a circle to any point on the boundary of the circle.
Diameter – Diameter is the line from one point on the boundary of the circle to another point and passing through the centre of the circle. It is twice the length of the radius.
Chord of a Circle – The chord of a circle is the line from one point on the boundary of the circle to another point. The diameter is the longest chord of a circle.
In the circle below,
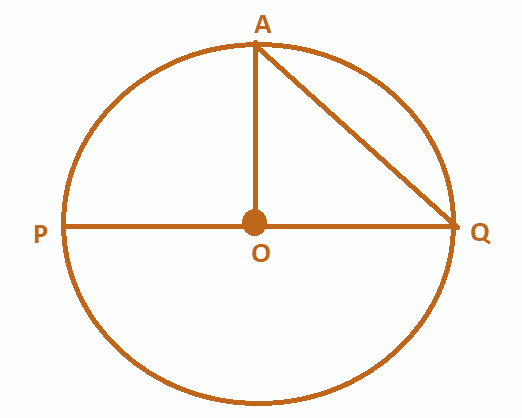
O is the centre of the circle.
The line segment AO is the radius of the circle.
The lone segment PQ is the diameter of the circle. Note that the line segment PQ is passing through the centre O
The line segment AQ is a chord of the circle that joins two points A and Q that lie on the boundary of the circle.
The curve formed by AQ is the arc of the circle.
X – axis
The x – axis is one of the two axes of that divides the coordinate system into two equal halves. Let us recall that the x-axis and the y-axis together divide the entire coordinate system into four equal parts which are called the quadrants of the coordinate system.
The line X O X ‘ is called the x-axis or axis of x and the line Y O Y ‘ is called the y-axis or the axis of y. The two lines X O X ‘ and Y O Y ‘ taken together are called the coordinate axis or the axis of the coordinate system. The point O is called the point of origin. This can also be represented as –
So, for example, in the graph of the coordinate axis that we have defined above, the two lines X O X ‘ and Y O Y ‘ divide the plane of the graph paper into four regions, namely, X O Y, X ‘ O Y , X ‘ O Y ‘ and Y ‘ O X. These four regions are called the quadrants.
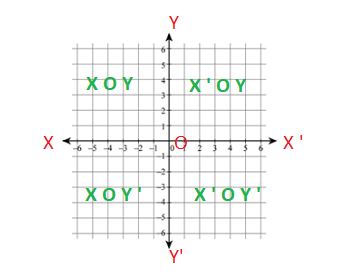
The ray O X ‘ is taken as a positive x-axis and the O X is taken as a negative x-axis. Similarly, the ray O Y is taken as a positive y-axis and the O y ‘ is taken as a negative y-axis.
Standard Equation of a Circle
The equation of the circle is derived from the equation of the circle and it has all the properties of the circle. In other words, the equation of a unit circle is represented using the second-degree equation with two variables x and y.
We know that the standard equation of a circle is given by
( x – a ) 2 + ( y – b ) 2 = r 2, where,
The centre of the circle is given by the point ( a, b ) and the radius of the circle is r.
Now, we will use the above equation to derive the general equation of the unit circle.
The above equation is known as the central form of the equation of a circle.
General Equation of a Circle
The equation of a circle whose centre is ( – g, – f ) and radius = $\sqrt{g^2+f^2 -c}$ is given by
x 2 + y 2 + 2 g x + 2 f y + c = 0.
Now, let us find the equation of a circle whose centre lies on the x – axis.
Equation of a Circle whose centre lies on x – axis
If the centre of a circle lies on the x – axis, say at a point ( a , 0 ), then what would be the equation of the circle? Let us find out.
We know that the standard equation of a circle is given by ( x – a ) 2 + ( y – b ) 2 = r 2, where the point ( a, b ) is the centre and the radius of the circle is r. now since the centre lies on the x – axis this means that the values of b shall be 0. Therefore, the centre of such a circle will be represented as –
( x – a ) 2 + ( y – b ) 2 = r 2
Substituting b= 0 in the above equation, we have,
( x – a ) 2 + y 2 = r 2
Expanding the equation further,
x 2 + y 2 – 2 a x + a 2 – r 2 = 0
Thus the equation of a circle whose centre lies on the x – axis will be x 2 + y 2 – 2 a x + a 2 – r 2 = 0
Let us understand this through an example.
Example
Find the equation of a circle of radius 5 whose centre lies on x – the axis and passes through the point ( 2 , 3 )
Solution
We know that the standard equation of a circle is given by ( x – a ) 2 + ( y – b ) 2 = r 2, where the point ( a, b ) is the centre and the radius of the circle is r. We have been given that the centre lies on x – the axis and passes through the point ( 2 , 3 ) and it has a radius 5.
Now, let the coordinates of the centre of the required circle be C ( a , 0 ). Since it passes through the point say, P ( 2 , 3 )
Therefore,
CP = radius
⇒ CP = 5
⇒ $\sqrt{( a-2 )^2+( 0-3 )^2}$ =
⇒ ( a-2 )2 + 9 = 25
⇒ a – 2 = ±4
⇒ a = 6 or a = – 2
Key Facts and Summary
- A circle is defined as the locus of a point that moves in a plane such that its distance from a fixed point in that plane is always constant.
- The fixed point is called the centre of the circle and the constant distance is called the radius of the circle.
- The standard equation of a circle is given by ( x – a )2 + ( y – b )2 = r2, where, The centre of the circle is given by the point ( a, b ) and the radius of the circle is r.
- The equation of a circle whose centre is ( – g, – f ) and radius = $\sqrt{g^2+f^2 -c}$ is given by x 2 + y 2 + 2 g x + 2 f y + c = 0.
- The equation of a circle whose centre lies on the x – axis will be x 2 + y 2 – 2 a x + a 2 – r 2 = 0
Recommended Worksheets
Spatial Skill: Circles (New Year’s Eve Themed) Math Worksheets
Circumference of a Circle (Summer Party Themed) Worksheets
Area of a Circle (Home Decorations & Furniture Themed) Worksheets









