Introduction
Geometry, a significant branch of mathematics, offers diverse concepts that help us understand the world around us. One such concept is the surface area of a cone. A cone is a three-dimensional geometrical figure with a single vertex and a circular base. The surface area of a cone refers to the whole or total area that the surface of the cone occupies. In this comprehensive article, we will delve into the concept, calculation, and application of the surface area of a cone.
Grade Appropriateness
The concept of surface area, including the surface area of a cone, is generally introduced to students in middle school, around 6th to 8th grade. However, the complexity of problems involving surface area can vary, allowing the topic to be explored at more advanced levels in high school.
Math Domain
The topic of the surface area of a cone falls under the domain of Geometry, which is a significant branch of mathematics concerned with questions of shape, size, the relative position of figures, and the properties of space.
Applicable Common Core Standards
The study of the surface area of a cone aligns with the following Common Core State Standards for Mathematics:
7.G.B.4: Know the formulas for the area and circumference of a circle and use them to solve problems.
7.G.B.6: Solve real-world and mathematical problems involving area, volume and surface area of two- and three-dimensional objects composed of triangles, quadrilaterals, polygons, cubes, and right prisms.
Definition of the Topic
The surface area of a cone is the measure of the total area that the surface of the cone occupies. The surface area includes the area of the base (which is a circle) and the lateral area (which is a sector of a larger circle).
Key Concepts
Radius: The radius (r) is the distance measured from the centre to the base’s edge.
Slant Height (l): The distance from the cone’s vertex (point) to the base’s edge.
Base Area (A): The area of the base of the cone, calculated by the formula A = πr².
Lateral Surface Area (A): The area of the cone, not including the base, is calculated by the formula A’ = πrl, where r is the radius, and l is the slant height.
Total Surface Area (T): The sum of the cone’s base area and the lateral surface area, calculated by the formula T = A + A’ = πr² + πrl = πr(r + l).
Discussion with Illustrative Example
Cones are 3D shapes. They have a circular base that narrows to a point at the other end, and they have a point at the other end.
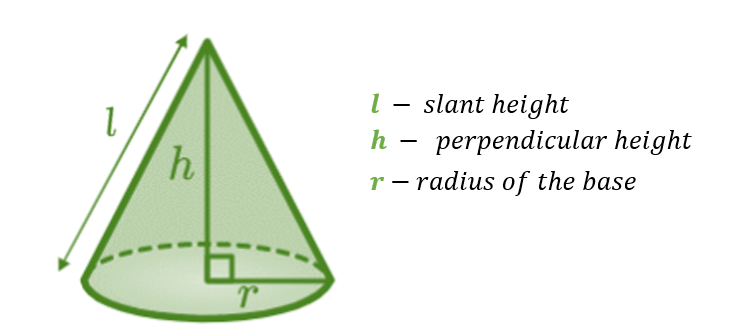
The total surface area of a cone refers to the area covering the outer surface of the cone. The illustration shows that l is the cone’s slant height, h is its perpendicular height, and r is its circular base’s radius.
The total surface area has two parts added together, the area of the curved surface and the area of the circular base.
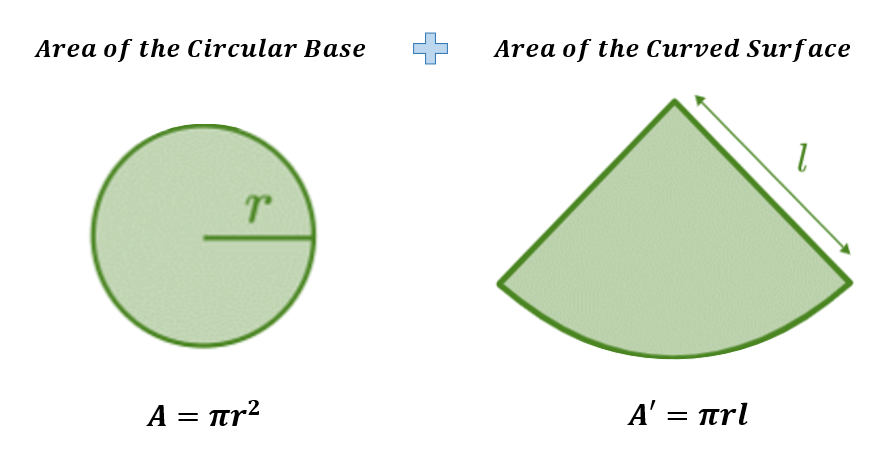
Surface Area of a Cone Formula

The total surface area of a cone is equal to the sum of the base area (A) and the lateral surface area (A’), calculated by the formula
T = A + A’ = πr² + πrl = πr(r + l).
Let’s consider a cone with a radius of 3 cm and a slant height of 5 cm.
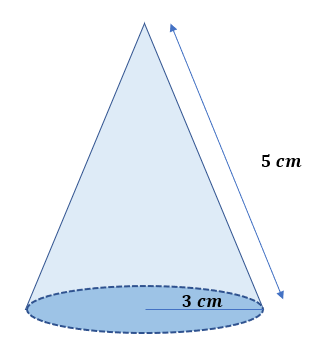
The base area (A) would be A = πr² =(π) (3 cm)² = 9π cm².
The lateral surface area (A) would be A’ = πrl =(π) (3 cm)(5 cm)=15π cm².
Then, the total surface area (T) would be T=A + A’ = 9π cm² + 15π cm² = 24π cm².
Remark:
The formula for the surface area of a cone shown above does not apply to oblique cones since the length of the slant lines is not constant.

The perpendicular height, h, of a cone, is not required in calculating the surface area but is used to solve the volume of a cone.
Examples with Solutions
Example 1
Calculate a cone’s total surface area (T) with a radius of 4 cm and a slant height of 6 cm.
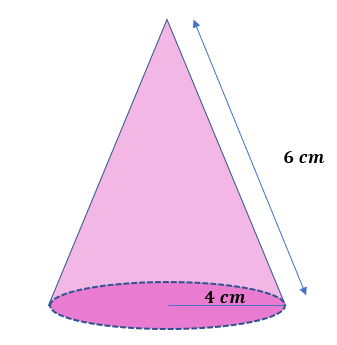
Solution
Here, r = 4 cm and l = 6 cm.
The total surface area T = πr(r + l) =(π) (4 cm) (4 cm + 6 cm)
T =(π) ( 4 cm) (10 cm) = 40π cm².
Hence, the total surface area is 40π cm².
Example 2
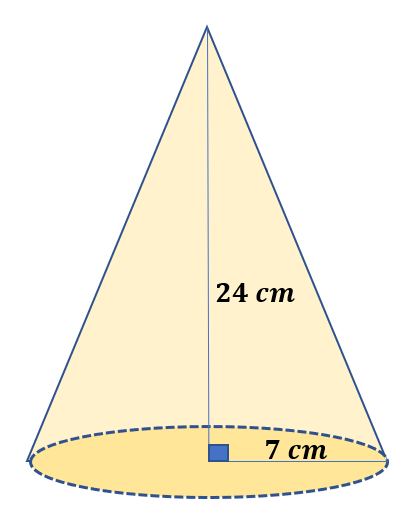
If the radius of a cone is 7 cm and its height is 24 cm, find the total surface area.
Hint: Use the Pythagorean Theorem to solve the slant height, l =$\sqrt{r^2+h^2}$.
Solution
Here, r = 7 cm and h = 24 cm. We need to find the slant height first.
l =$\sqrt{r^2+h^2}$
l=$\sqrt{(7 cm)^2+(24 cm)^2}$
l=$\sqrt{49 cm^2+576 cm^2}$
l=$\sqrt{625 cm^2}$
l=25 cm
Then, the total surface area T = πr(r + l) =(π )( 7 cm) (7 cm + 25 cm) = 224π cm².
Given a cone, with r as the radius of the circular base and h as its height, the formula for getting the total surface area (T) of a cone is:
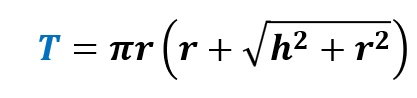
Example 3
Find the surface area of each given cone. Use π=3.14 and round off the answers to the nearest tenths.
a. r = 3 cm and l = 6 cm
b. r = 2 m and l = 8 m
c. r = 6 ft and h = 8 ft
Solution
a. r = 3 cm and l = 6 cm
T= πr(r + l)
T=(π)(3 cm)(3 cm+6 cm)
T=27π cm2
T=(27)(3.14)cm2
T=84.78 cm2
b. r = 2 m and l = 8 m
T= πr(r + l)
T=(π)(2 m)(2 cm+8 m)
T=20π m2
T=203.14m2
T=62.80 m2
c. r = 6 cm and h = 8 cm
T=πr (r+$\sqrt{h^2+r^2}$)
T=(π)(6 cm )(6 cm+$\sqrt{(8 cm)^2+(6 cm)^2}$)
T=(6π cm)(6 cm+$\sqrt{64 cm^2+36 cm^2}$)
T=(6π cm)(6 cm+10 cm)
T=96π cm2
T=(96)(3.14)cm2
T=301.44 cm2
Real-life Application with Solution
Cone-Shaped Tent: Suppose you want to make a cone-shaped tent. The tent’s slant height is 12 feet, and its base has a radius of 5 feet. How much material will you require to make the tent?
Solution
The material needed for the tent is equal to the total surface area of the cone-shaped tent. Here, r = 5 feet and l = 12 feet.
The total surface area T = πr(r + l) =(π) (5 feet) (5 feet + 12 feet)
T=85π square feet
So, you will need 85π square feet of material to make the tent.
Practice Test
1. Sove the total surface area of a cone with a slant height of 4 cm and radius of 3 cm.
2. If the radius of a cone is 8 cm and its height is 15 cm, find the total surface area.
3. A cone has a total surface area of 314 cm² and a radius of 7 cm. Find its slant height.
4. How much material is needed to make a cone-shaped hat with a radius of 6 inches and a slant height of 10 inches? Use π=3.14.
5. Find the radius and slant height if a cone has a base area of 28.26 cm² and a total surface area of 94.2 cm².
Answers:
1. 21π cm²
2. 200π cm²
3. 7.28 cm
4. 301.44 in²
5. r=3 cm and l=7 cm
Frequently Asked Questions (FAQs)
What is the difference between a cone’s lateral surface area and base area?
A cone’s lateral surface area refers to the cone’s surface area, excluding the base. A cone’s base area refers to the circular base’s area.
How is the slant height of a cone different from the height?
A cone’s slant height is the measurement down the side of the cone from the vertex, or top point, to the base’s edge. The height of the cone refers to the distance of the centre of the base from the vertex, directly through the cone’s interior.
Can I find the total surface area of a cone if I only know the radius and the height?
Yes, you can find the total surface area given a cone’s radius and height. You need to calculate the slant height using the Pythagorean theorem, l=$\sqrt{r^2+h2}$, and then use the computed value to find the total surface area.
Does the formula for the total surface area of a cone applicable to all cones?
The formula, T = πr(r + l), applies to all right circular cones where the axis is perpendicular to the base of the cone. The formula changes for non-right or oblique cones due to the different orientations of the height and slant height.
Is the surface area of a cone always measured in square units?
Yes, the surface area of a cone, like all areas, is always measured in square units. Some examples could be square centimetres, square meters, square feet, or any other square unit appropriate to the problem.
Recommended Worksheets
Surface Area of a Cone (Christmas Themed) Math Worksheets
Lateral Surface Area of a Cone (Day of the Dead Themed) Math Worksheets
Surface Area of a Sphere (Songkran Festival Themed) Math Worksheets









