What will I learn from this article?
After reading this article, you will be able to:
- properly define corresponding angles;
- know the corresponding angle theorem;
- determine corresponding angles based on figures;
- prove the corresponding angle theorem;
- prove the converse of the corresponding theorem; and
- apply the theorems in solving problems involving corresponding angles.
What are corresponding angles?
When another line, called a transversal line, intersects two distinct lines, the angles in the corners formed in the point of intersections are referred to as corresponding angles. Corresponding angles are found at the intersection of two or more straight lines in the same relative position.
Corresponding angles formed by non-parallel lines
If there exist at least two non-parallel lines that are not equal, then the corresponding angles that exist between them don’t have any relation and are not congruent.
For example, line 1 and line 2 are non-parallel lines cut by a transversal line, line 3.
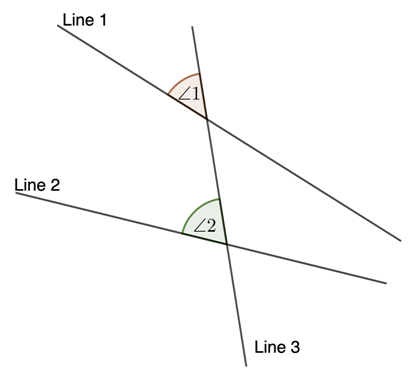
Thus, we can say that ∠1 and ∠2 are corresponding angles. However, the measures of those angles are not related to each other.
Corresponding angles formed by parallel lines
When two parallel lines intersect with a third line (transversal line), the angles that share the same relative position at each intersection are said to be corresponding angles.
Say, for example,
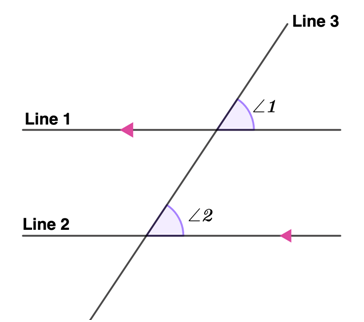
The figure above describes corresponding angles. Thus, interpreting the figure:
- Line 1 and Line 2 are parallel lines;
- Line 3 intersects with Lines 1 and 3;
- Angles 1 and 2 have the same relative position.
Thus, we can conclude that angles 1 and 2 are corresponding angles.
What are the theorems about corresponding angles?
There are two theorems about corresponding angles.
Corresponding Angle Theorem
The corresponding angle theorem states that,
If a line intersects two parallel lines, then the corresponding angles in the two intersections are congruent.
Say, for example,
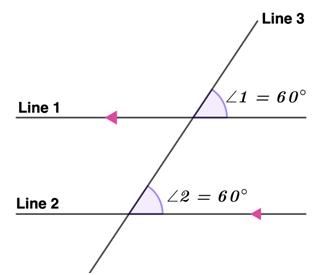
In the figure, since we know that line 1 ∥ line 2 and line 3 is the transversal line, then ∠1 is corresponding to ∠2. Hence, we can say that the angle that exists between them is equal. Thus, if ∠1=60° then, ∠2=60°.
Converse of Corresponding Angle Theorem
The converse of a corresponding angle theorem states that,
If the corresponding angles in the two intersection regions are congruent then, the two lines are said to be parallel.
Take Note:
- A pair of corresponding angles lie on the same side of the transversal line.
- One exterior angle and one interior angle comprise up the corresponding pair of angles.
- Not all corresponding angles are equal. If the transversal intersects two parallel lines, the corresponding angles are equal. When the transversal intersects non-parallel lines, the resulting angles are incongruent and unrelated.
- Supplementary angles are formed when the transversal perpendicularly intersects two parallel lines.
- If the lines are parallel, exterior angles on the same side of the transversal are supplementary. Similarly, if the two lines are parallel, the interior angles are supplementary.
What are the proofs on the theorems of corresponding angles?
Proof of the corresponding angle theorem
Assume line A and line B are parallel.
Prove that the corresponding angles are equal.
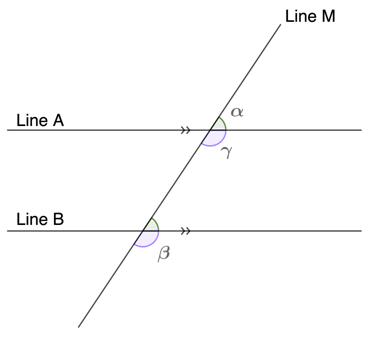
Suppose line A is parallel to line B. If a distinct line M intersects with lines A and B, then we can label the angles α,β, and γ, as shown in the figure.
By the definition of corresponding angles, we can say that γ is corresponding to β.
Since α and γ are in a straight line, by linear pair postulate, we can conclude that the sum of α and γ is 180°. Thus, γ=180°-α.
Since β and α form the interior and exterior angles of the parallel lines, it also follows that β is supplementary to α. Thus, we can conclude that β=180°-α. Then, we will have
γ=180°-α; and β=180°-α.
Hence, γ=β.
Therefore, the pair of corresponding angles are equal to each other.
Proof of the converse of the corresponding angle theorem
Assume the corresponding angles are equal.
Prove that line P and line Q are parallel.

Suppose two distinct lines P and Q are cut by a transversal line T and assuming that the corresponding angles are equal, then we can label angles as α and β, as shown in the figure.
By linear pair postulate, we can label every pair of corresponding angles as either α or β. Since for every pair of angles α and β, the sum is 180°, and the alternate interior angles are equal. Thus, by the converse of the same side interior angle theorem, line P and line Q are parallel.
Therefore, $\overleftrightarrow{P} ∥ \overleftrightarrow{Q}$.
How to find corresponding angles?
If two parallel lines are cut by a transversal line then, each intersection points create four angles. Thus, if each of the four angles in the first intersection region then, it will have another one with the same relative position in the second intersection.
Let’s look at the sample below.
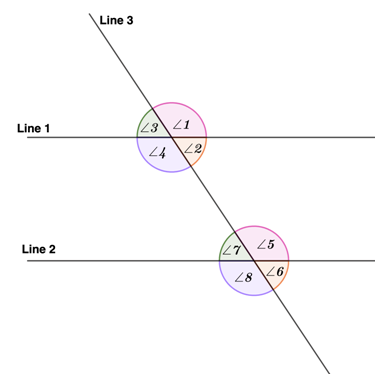
In the given figure, the angles corresponding to each other are,
- ∠1 and ∠2 where both angles are positioned on the upper right side of Line 1 and Line 2;
- ∠2 and ∠6 where both angles are positioned on the lower right side of Line 1 and Line 2;
- ∠3 and ∠7 where both angles are positioned on the upper left side of Line 1 and Line 2; and
- ∠4 and ∠8 where both angles are positioned on the upper left side of Line 1 and Line 2.
Example #1
Determine the corresponding angles in the figure.
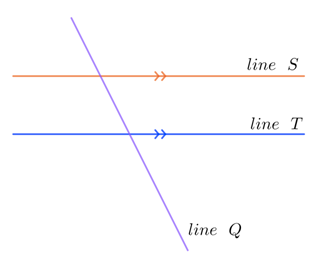
Solution
In the given figure where Line S and Line T are parallel to each other, they are cut by a transversal Line Q. Thus, by the corresponding angle theorem,
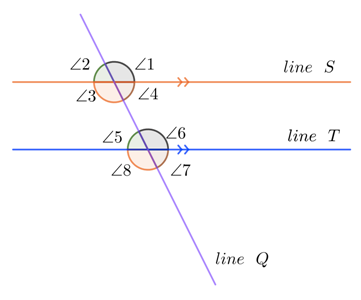
By creating angles from the point of intersections of line S and line Q, and line T and Line Q, we will have the following angles as corresponding to each other.
- ∠1 is corresponding to ∠6;
- ∠2 is corresponding to ∠5;
- ∠3 is corresponding to ∠8; and
- ∠4 is corresponding to ∠7.
Example #2
Determine the corresponding angles in the figure below.
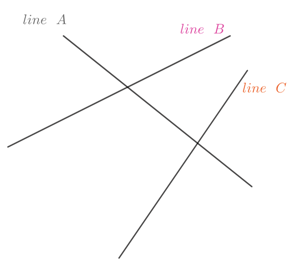
Solution
In the figure, we can notice that a transversal line B intersects with lines A and C that are not parallel. Thus, the corresponding angles are:
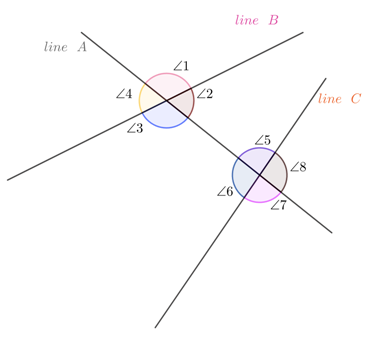
- ∠1 is corresponding to ∠5;
- ∠2 is corresponding to ∠8;
- ∠3 is corresponding to ∠7; and
- ∠4 is corresponding to ∠6.
While they may be corresponding to each other, the measures of their angles are not relevant to each other.
Example #4
Consider the window below. Determine the corresponding angles that can be formed inside the window. How many pairs of corresponding angles are there inside the window?

Solution
By the definition of corresponding angles, we can name each pair of corresponding angles in the windows as:
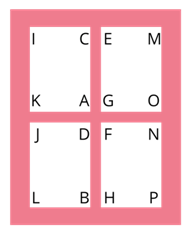
Thus,
- ∠A is corresponding to ∠B;
- ∠C is corresponding to ∠D;
- ∠E is corresponding to ∠F;
- ∠G is corresponding to ∠H;
- ∠I is corresponding to ∠J;
- ∠K is corresponding to ∠L;
- ∠M is corresponding to ∠N; and
- ∠O is corresponding to ∠P
Therefore, there are 8 pairs of corresponding angles inside the window.
Solving problems involving corresponding angles
To solve problems involving corresponding angles:
- Determine the corresponding angles.
- Use the corresponding angle theorem that states that corresponding angles are congruent.
Example #1
Determine the angle measure of ∠1 if line 1 ∥ line 2 and is cut by a transversal line.
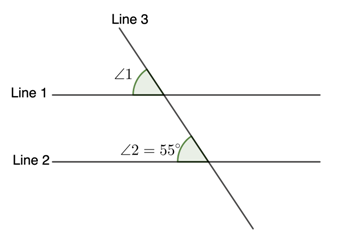
Solution
As stated in the problem, there exist lines 1 and 2 that are parallel to each other and were cut by a transversal line, line 3. The given figure says that ∠2=55°. Thus, by corresponding angle theorem, ∠1=55°.
Therefore, ∠1=55°.
Example #2
What is the measure of ∠2 and value of x based on the given figure?
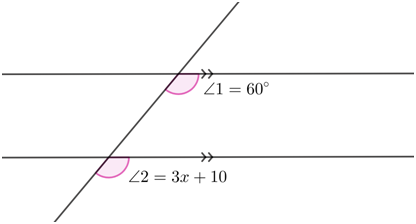
Solution
Based on the figure, we can say that ∠1 and ∠2 are corresponding to each other. Thus,
∠1=∠2. By substitution,
∠1=∠2
60=3x+10
3x=60-10
3x=50
x=16.67
Therefore, the value of x is 16.67 and the measure of ∠2=60°.
Example #3
Consider the figure below. Determine the value of x and the angle measures of ∠2 and ∠4 if the roads are parallel to each other.

Solution:
As stated in the problem, the two roads are parallel to each other. Thus, ∠1 corresponds to ∠2, and ∠3 corresponds to ∠4.
Step 1: Find the angle measure of ∠2. By corresponding angle theorem, if two angles are corresponding to each other, and the lines between them are parallel then, they are congruent. Thus, if ∠1=110° then, ∠2=110°.
Step 2: Find the value of x in ∠4=13x+5. Since ∠3 corresponds to ∠4, then
∠3 = 4
70 = 13x + 5
13x =70-5
13x=65
13x/13 = 65/13
x = 5
Therefore, the angle measure of ∠2=110° and ∠4=70°. The value of x is 5.
What is the significance of corresponding angles?
Numerous applications of corresponding angles go unnoticed, such as:
- Windows are equipped with horizontal and vertical grills that create multiple squares. Each vertex of the square corresponds to one of the angles.
- Bridges are supported by the pillars. Each pillar is connected in such a way that the angles of the corresponding pillars are equal.
- Railway tracks are designed in such a way that all corresponding angles on the track are equal.
Recommended Worksheets
Obtuse Triangles (Toy Store Themed) Math Worksheets
Scalene Triangles (Summer Camp Themed) Math Worksheets
Parallel lines Cut by a Transversal 8th Grade Math Worksheets









