Introduction
A tetrahedron is a fascinating shape belonging to the platonic solids family. It might sound like a complex term, but fear not! This article will break it down into fun, bite-sized information so you can quickly grasp the concept.
Grade Appropriateness
The study of a tetrahedron is most suitable for students aged between 8 and 15 years old, typically those studying in the 4th to 9th grade. It’s an excellent way to explore the beauty of geometry and its various applications in the real world.
Math Domain
The tetrahedron belongs to the math domain of Geometry. Geometry deals with different shapes, sizes, the properties of space, and the relationships between different shapes.
Applicable Common Core Standards
The exploration of a tetrahedron aligns with the following Common Core Standards:
CCSS.Math.Content.6.G.A.4: Represents three-dimensional figures using nets made up of rectangles and triangles, and use the nets to find the surface area of these figures.
CCSS.Math.Content.7.G.B.6: Solves real-world and mathematical problems involving area, volume, and surface area of two- and three-dimensional objects composed of triangles, quadrilaterals, polygons, cubes, and right prisms.
Definition of the Topic
A tetrahedron is a solid geometric figure with four faces; each face is an equilateral triangle. It also has four vertices (or corners) and six edges. Imagine you’re holding a pyramid, but instead of a square base, you have a triangle base. That’s a tetrahedron!

Key Concepts
Regular Tetrahedron: A regular tetrahedron has four faces that are equilateral triangles, six edges of equal length, and four vertices.
The volume of tetrahedron: The formula to calculate the volume of a regular tetrahedron is:
Volume=$\frac{a^3\sqrt{2}}{12}$, where a is the length of the edge.
The total surface area of a tetrahedron: The formula to find the total surface area of a regular tetrahedron is:
Total Surface Area=$\sqrt{3}$ a2, where a is the length of the edge.
The lateral surface area of a tetrahedron: The formula to find the lateral surface area of a regular tetrahedron is:
Lateral Surface Area=$\frac{3\sqrt{3}}{4}$a2, where a is the length of the edge.
Discussion with Illustrative Examples
Let’s imagine a regular pyramid with a triangular base (remember, all sides of this triangle are equal).

This pyramid is a tetrahedron. Every corner of the triangle is attached to a single point. Each of these lines forms an edge. So, a tetrahedron is formed.
The Greek term “tetráedron,” where “tetrás” stands for “four”, and “hédra” for “seat,” is where the English word “tetrahedron” is derived.
Tetrahedrons are polyhedra that have four triangular faces, six edges, and four vertices. All of the faces of a tetrahedron are equilateral triangles. One of its faces is the base, while the other three form the pyramid. As a result, a tetrahedron is also known as a triangular pyramid.
Parts and Properties of a Tetrahedron
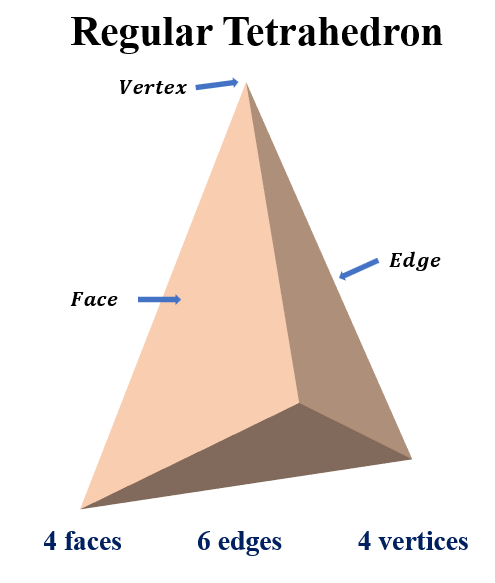
| To help us identify this shape, the following are the properties of a tetrahedron: A tetrahedron has four faces. Each face is an equilateral triangle, meaning all sides and angles are equal. An edge is the section of a line where two faces intersect. A tetrahedron has six edges. The corners of a tetrahedron, where the faces meet, are called vertices. There are four vertices in a tetrahedron. All four vertices are equidistant from each other. A tetrahedron has no parallel faces. A regular tetrahedron has four triangles as its faces. It has six planes of symmetry. An imaginary plane known as a plane of symmetry divides a shape into two mirrored parts. |
Below is an example of a regular tetrahedron.
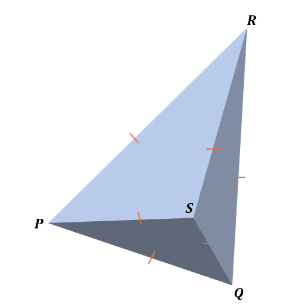 | The four vertices are corners P, Q, R, and S. The six edges are segments PQ, PS, PR, QR, QS, and RS. The four triangular faces are triangles PQS, QSR, PQR, and PSR. No parallel faces It has six planes of symmetry. |
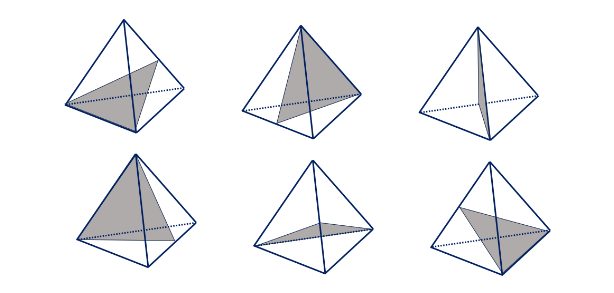
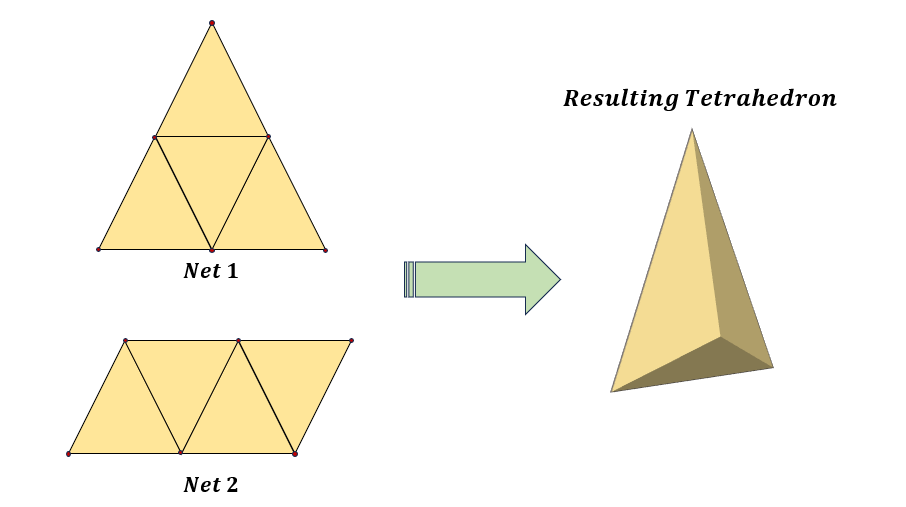
Nets of a Tetrahedron
A tetrahedron is a three-dimensional shape that can be created with a geometric net. In geometry, a net is a two-dimensional shape that, when folded in a specific way, produces a three-dimensional shape.
A tetrahedron has two (2) distinct nets. It has four equilateral triangular faces on its net.
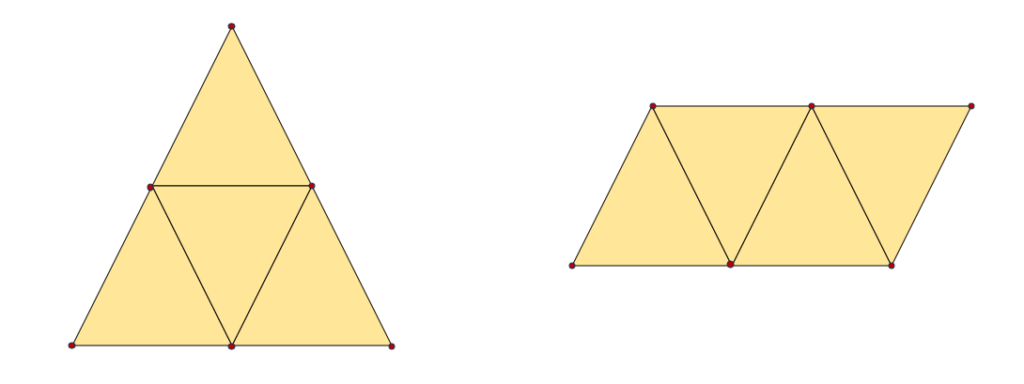
Folding the two distinct tetrahedron nets shown above will result in the formation of a tetrahedron.
Formulas Involving a Tetrahedron
Surface Area of a Tetrahedron
The total area covered by the faces of a tetrahedron is defined as its surface area. Surface areas of a regular tetrahedron can be of two types:
Total Surface Area. The total surface area of a tetrahedron is the surface area of all its faces. The formula for calculating the total surface area of a regular tetrahedron is:
Total Surface Area=$\sqrt{3}$ a2, where a is the length of the edge.
Lateral Surface Area. The lateral surface area of a tetrahedron is the surface area of its lateral or slant faces. The formula to determine the lateral surface area of a regular tetrahedron is:
Lateral Surface Area=$\frac{3\sqrt{3}}{4}$a2, where a is the length of the edge.
The total surface area (TSA) and lateral surface area (LSA) of a tetrahedron is expressed in square units (e.g., square centimetres, square feet, and square inches).
Volume of a Tetrahedron
The volume of a tetrahedron is the total space it occupies in a three-dimensional plane.
The formula for calculating the volume of a regular tetrahedron is given by:
Volume=$\frac{a^3\sqrt{2}}{12}$, where a is the length of the edge.
On the other hand, the volume of a tetrahedron is expressed in cubic units (e.g., cubic centimetres, cubic feet, and cubic inches).
Examples with Solution
Example 1:
If each tetrahedron edge measures 4 cm, what is its total edge length?
Solution
A tetrahedron has six edges. Therefore, if each edge is 4 cm, the total edge length is 6×4 cm=24 cm.
Example 2
Find the total surface area and the lateral of the tetrahedron below.
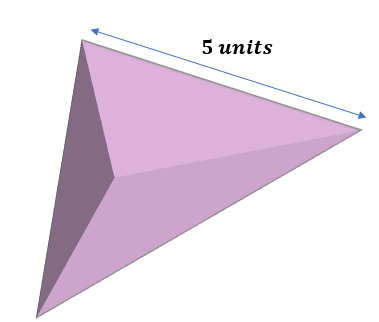
Solution
Since the measure of each edge of the given regular tetrahedron is a=5 units, we have,
Total Surface Area=$\sqrt{3}$ a2
Total Surface Area=$\sqrt{3}$ (5)2
Total Surface Area=25$\sqrt{3}$
Total Surface Area=43.30 square units
Lateral Surface Area=$\frac{\sqrt{3}}{4}$ a2
Lateral Surface Area=$\frac{\sqrt{3}}{4}$ (5)2
Lateral Surface Area=25$\frac{\sqrt{3}}{4}$
Lateral Surface Area=10.83 square units
Therefore, the total surface area of a regular tetrahedron with an edge length of 5 units is approximately 43.30 square units, while its lateral surface area is approximately 10.83 square units.
Example 3
Calculate the volume of a regular tetrahedron with an edge length of 7 cm.
Solution
Plugging in the given edge length, a=7 cm, into the formula, we have,
Volume= $\frac{a^3\sqrt{2}}{12}$
Volume= $\frac{7^3\sqrt{2}}{12}$
Volume= $\frac{343\sqrt{2}}{12}$
Volume≈40.42 cm2
Hence, the volume of a regular tetrahedron whose side length is 7 cm is approximately 40.42 cm2.
Example 4
Find the volume of a regular tetrahedron if its total surface area is 64√3 square units.
Solution
Since we know that the TSA is 64√3 square units, let us first calculate the edge length of the tetrahedron. Using the formula for getting the total surface area we have,
√3a2 = 64√3
$\frac{\sqrt{3}a^2}{\sqrt{3}}$ = $\frac{64\sqrt{3}}{\sqrt{3}}$ (Dividing both sides by √3)
a2 = 64 (Simplify)
√a = √64
a=8 units (Edge length)
Now, using the formula for getting the volume of a regular tetrahedron, we shall have,
Volume=$\frac{a^3\sqrt{2}}{12}$
Volume=$\frac{8^3\sqrt{2}}{12}$
Volume=$\frac{512\sqrt{2}}{12}$
Volume≈60.34 cubic units
Therefore, the volume of a regular tetrahedron is 60.34 cubic units if TSA is 64√3 square units.
Real-life Application with Solution
Tetrahedrons are often used to design structures like bridges and towers due to their strength and stability. If you’ve seen the game “Jenga,” you’ll notice that the most stable structure you can build may form a tetrahedron-like shape.
Problem
Thalia has a regular tetrahedron-shaped toy block. If each of its edges measures 3 inches, find its lateral surface area, total surface area, and volume.
Solution
Since the =3 inches, we shall directly substitute it into the formulas to calculate the surface area and volume. Hence we have,
| Lateral Surface Area LSA=$\frac{3\sqrt{3}}{4}$ a2 LSA=$\frac{3\sqrt{3}}{4}$ (3)2 LSA=$\frac{27\sqrt{3}}{4}$ LSA≈11.69 in2 | Total Surface Area TSA=√3 a2 TSA=√3 (3)2 TSA=9√3 TSA≈15.59 in2 | Volume V=$\frac{a^3\sqrt{2}}{12}$ V=$\frac{3^3\sqrt{2}}{12}$ V=$\frac{9\sqrt{2}}{4}$ V≈3.18 in3 |
Practice Test
1. How many vertices does a tetrahedron have?
2. If a tetrahedron has an edge length of 4 cm, what is its total surface area?
3. True or False: All faces of a regular tetrahedron are equilateral triangles.
4. How many edges does a tetrahedron have?
5. What is the volume of a regular tetrahedron with an edge length of 10 units?
Answers:
1. A tetrahedron has four vertices.
2. Total Surface Area=√3 a2=√3 (4)2=16√3≈27.71 cm2
3. True
4. A tetrahedron has six edges.
5. Volume=$\frac{a^3\sqrt{2}}{12}$=$\frac{10^3\sqrt{2}}{12}$=$\frac{1000\sqrt{2}}{12}$=$\frac{250\sqrt{2}}{3}$≈117.85 cubic units
Frequently Asked Questions (FAQs)
Is a tetrahedron a type of pyramid?
Yes. A tetrahedron is a type of pyramid. It is a pyramid with a triangular base.
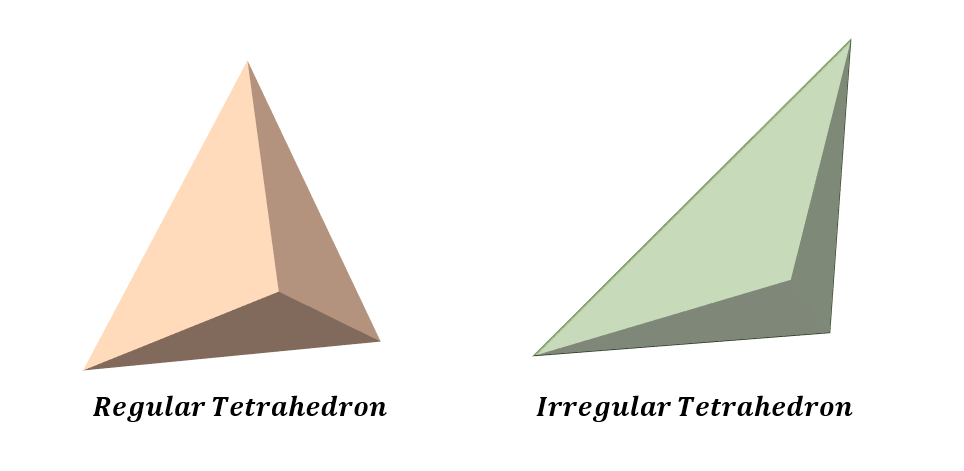
Can a tetrahedron have faces that are not equilateral triangles?
For a regular tetrahedron, all the faces are equilateral triangles. However, in an irregular tetrahedron, the faces can be any triangle.
Why is the tetrahedron important in geometry?
The tetrahedron is the simplest polyhedron (a 3D shape with flat faces). Due to its strength and stability, it is used to understand more complex shapes and in various real-world applications.
Does a tetrahedron have any axes of symmetry?
A regular tetrahedron has several axes of symmetry. Any line through the centre and a vertex is an axis of symmetry.
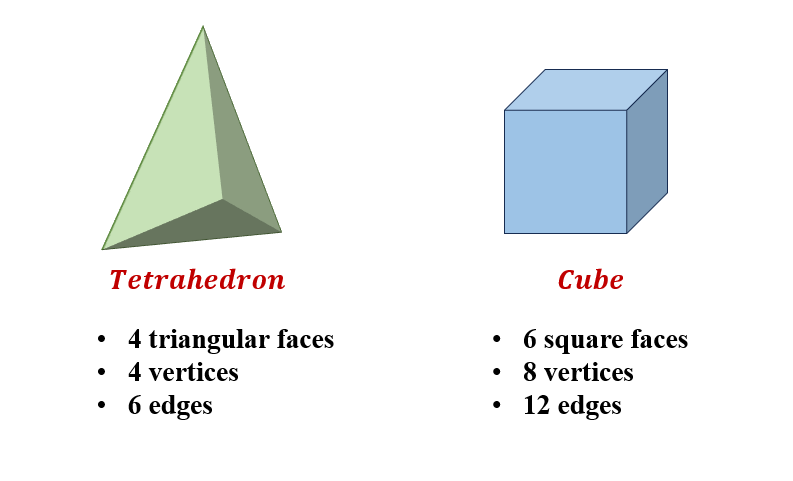
What’s the difference between a tetrahedron and a cube?
A tetrahedron and a cube are both polyhedrons but differ in their structures. A tetrahedron has four vertices, six edges, and four faces that are all equilateral triangles. On the other hand, a cube has eight vertices, 12 edges, and six faces, all of which are squares.
Recommended Worksheets
Tetrahedron (Earth Hour Themed) Math Worksheets
Platonic Solids (Earth Day Themed) Math Worksheets
Icosahedron (Holi Themed) Math Worksheets









