Introduction
Before we begin discussing the factors of 28, let us clarify some confusion between the terms “Factors” and “Multiples”.
By definition, factors are numbers used to multiply to get a product. Whereas multiples are products that are multiplied by factors. This means that to divide a multiple evenly, we need factors. To conclude, factors are needed to get a product, while multiples are products.
The same thing goes with the differences of “Factors of 28” and “Multiples of 28”. But before we discover the numbers that comprise each one of them. Let us now begin discussing the different strategies on how to find the Factors of 28.
Pairs of Factors of 28
Often, pairs of factors come in positive integers. So, let us talk about how to get the pairs of positive integer factors of 28.
Technique 1: Prime Factorization Using Factor Tree and Tabular Division
By using a factor tree, we can break down the factors of 28 by having its smallest prime factor and its partner factor. Since 28 is an even number, 2 is its smallest prime factor by default. This means that 2’s partner factor is 14, because 28 ÷ 2 = 14.
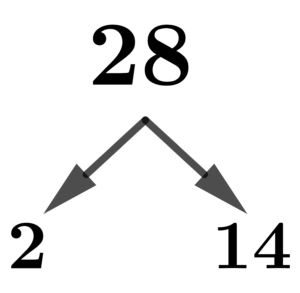
Hence, the first pair of factors of 28 is 2 and 14. But 14 is still a composite number, this means that we can still split it up into factors. Again, 14 is an even number, so we need to divide it also by 2 having 7 as its partner factor.
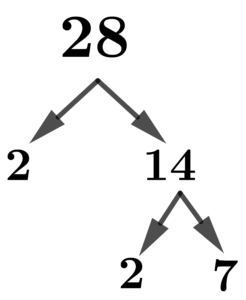
Since 7 is also a prime number, we can now end the process. We can notice that have two levels of branches of the factor tree. This means that we have 2 pairs of factors using the factor tree. But we need to add 1 and 28 as factors as well even it is not formally written, because we can still get 28 by multiplying 1 by 28. 1 was not written in the prime factorization, because it is not a prime number.
Getting the first level as factors, we have:
28 = 2 × 14
As for the second level of the branches, we need to include to first prime factor written in the first level.
28 = 2 x 2 × 7
28 = 4 7
Scraping all of the numbers that we got, we 3 pairs (or 6 in total) of positive integer factors of 28: (1, 28), (2, 14), and (4, 7).
Aside from the Factor Tree, we can also do the Prime Factorization through the Tabular Division Method.
We need to start by drawing a table with 2 columns, putting 28 to the right.
| 28 |
Then, we are going to write the divisor into the left, which needs to be the dividend’s smallest prime factor. Since 28 is an even number, 2 is its lowest prime factor. Thus, we are going to use 2 as 28’s divisor.
| 2 | 28 |
Before dividing 28 by 2, we need to add another row to make space for the quotient.
| 2 | 28 |
28 ÷ 2 = 14. Now that we have a quotient, we are going to put it beneath 28. But since 14 can still be divided by 2, we are going to repeat the process until reaching a quotient of 1.
| 2 | 28 |
| 2 | 14 |
| 7 | 7 |
| 1 |
Now that we have reached the quotient of 1, we can now stop the process and get the factors. The first factors are the first divisor (2) and the first quotient (14).
| 2 | 28 |
| 2 | 14 |
| 7 | 7 |
| 1 |
28 = 2 × 14
Then, the next pair of factors are the first two prime factors (2 and 2) and the second quotient.
| 2 | 28 |
| 2 | 14 |
| 7 | 7 |
| 1 |
28 = 2 x 2 × 7
28 = 4 x 7
Lastly, the last pair of factors are the product of all divisors (2, 2, and 7) and the last quotient (1).
| 2 | 28 |
| 2 | 14 |
| 7 | 7 |
| 1 |
28 = 2 x 2 × 7 x 1
28 = 28 x 1
Gathering all the information, we have 3 pairs of factors (6 in total) of 28 that are positive integers: (2, 14), (4, 7), and (28, 1).
Technique 2: Using the Rules of Divisibility
If a number is divisible by another number, this means that another number can divide the first number evenly or without remainder. And since Division is the inverse of Multiplication, we can identify the pair factors of 28 by dividing it by the number it is divisible by.
Furthermore, by using the Divisibility Rules, we can know immediately the factors of a number without tedious methods. We just need to be familiar with each rule so that we can know whether a number is divisible by 2 until 10.
Here is the list of the Rules of Divisibility from 2 until 10:
| Divisible by | If | So, is it divisible by 28? | Why? |
| 2 | a number is an even number | Yes | 28 is an even number |
| 3 | the sum of the digits is divisible by 3 | No | 2 + 8 = 10; 10 is not divisible by 3. |
| 4 | the last two digits are divisible by 4 | Yes | 28 only 2 digits, and it is divisible by 4. |
| 5 | the number ends with 0 or 5 | No | 28 ends with 8, not 0 nor 5. |
| 6 | the number is divisible by both 2 and 3 | No | 28 is divisible by 2 but not by 3. |
| 7 | we got a difference that is also divisible by 7 by subtracting the last digit’s number and 2’s product | Yes | 28’s last product is 8, so 8 × 2 = 16 Then, 2 – 16 = -14, where -14 is divisible by 7. |
| 8 | the last three digits of the number are also divisible by 8 | No | 28 is not divisible by 8 |
| 9 | the sum of the digits is divisible by 9 | No | 2 + 8 = 10, and 10 is not divisible by 9. |
| 10 | the number ends with 0 | No | 28 does not end with 0. |
Gathering the data above, we found out that 28 is divisible by 2, 4, and 7.
Now, to find the co-factor of each number, we are going to divide 28 by each number.
First pair:
28 ÷ 2 = 14
Thus, the first pair of factors of 28 are 2 and 14, because 2 x 14 = 28.
Second Pair:
28 ÷ 4 = 7
Hence, the second pair of factors of 28 are 4 and 7, because 4 × 7 = 28.
Since we got 7 as quotient by dividing 4 from 28, it is fine to stop the process. The reason for this is the Commutative Property of Multiplication, wherein whatever the arrangement of the factors is, we can still get the same product.
4 × 7 = 28
7 × 4 = 28
With that in mind, we can are going to count them as one pair of factors still.
Lastly, every number is divisible by 1. So, we are going to consider 1 and 28 as the last pair of factors of 28.
Overall, the 3 pairs of positive integer factors of 28 are (2, 14), (4, 7), and (1, 28).
Listing the Factors
The formal convention or way of writing the factors of a number is by listing them as elements starting from least to greatest. It is easy to start with 1 and 28, but sometimes, it is confusing where we should put the other factors. But now that we are familiar with the factors of 28, we can now list them from least to greatest.
The strategy is writing 1 as the first element and 28 as the last element.
28 = {1, 28}
Then, write the pair that is greater than 1 as the second and second to last of the elements.
28 = {1, 2, 14, 28}
Lastly, write the last pair as the inner elements.
28 = {1, 2, 4, 7, 14, 28}
By this convention, we can easily notice that there are 6 factors of 28 that are positive integers.
Prime Factors of 28
For us to know the prime factors of 28, let us go back to the prime factorization using the Tabular Method. This is an easy way to know the prime factors because we are just going to get the numbers in the first column.
| 2 | 28 |
| 2 | 14 |
| 7 | 7 |
28 = 2 x 2 × 7
So, the prime factors of 28 are 2, 2, and 7 or 22 and 7.
Be careful not to consider the list of the factors of 28 to get the prime factors because if we get only 2 and 7, we cannot obtain a product of 28.
28 = {1, 2, 4, 7, 14, 28}
28 ≠ 2 × 7
Proper Factors of 28
Proper Factors are factors of a number without the number itself. Because of that, there are only five proper factors of 28: 1, 2, 4, 7, and 14.
Sum of the Factors 28
Here are the factors of 28:
28 = {1, 2, 4, 7, 14, 28}
Summing all of them, we have:
1 + 2 + 4 + 7 + 14 + 28 = 56
Thus, the sum of the factors of 28 is 56.
Is 28 Abundant, Perfect, or Deficient Number?
An abundant number is a number where the sum of its proper factors is greater than the number. A number is perfect if this number is equal to the sum of its proper factors. On the other hand, a number is deficient if the sum of its proper factors is less than the number itself.
So, in order for us to know what kind of number 28 is, we need to add all of its proper factors.
1 + 2 + 4 + 7 + 14 = 28
Since 28 is the sum of the proper factors of 28, this number is perfect.
Factors of 28 that are Negative Integers
From the factor’s definition, these must be the numbers that when multiplied, will obtain a product. The same thing goes in negative integers. By default, we can get a product that is a positive integer if we multiply integers that are either both negative or positive. So, in order to get the negative integer factors of 28, we must transform each one of the positive factors into negative factors.
28 = {1, 2, 4, 7, 14, 28}
28 = {-1, -2, -4, -7, -14, -28}
Multiplying each pair of the negative integer factors, we can still get a product of 28.
-1 x -28 = 28
-2 x -14 = 28
-4 x -7 = 28
So, there are 3 pairs (6 in total) of factors of 28 that are negative integers.
Factors of 28 that are in Fractions
Unlike integers, fractions are measured without exactness. Because of that, we can have an infinite number of factors that are in fractions. For instance, if we try Tabular Division again, we could have an unending result. Since 28 is an even number, its lowest prime factor is 2. But in this case, we need to reciprocate the prime factor that will serve as the first divisor to make it a fraction.
2 reciprocal -> $\frac{1}{2}$
So, we are going to use $\frac{1}{2}$ as the starting divisor.
| $\frac{1}{2}$ | 28 |
Next, proceed with the process of division of fractions.
28 ÷ $\frac{1}{2}$ → 28 × $\frac{2}{1}$ → 56
28=$\frac{1}{2}$ ×56
Write the quotient beneath 28.
| $\frac{1}{2}$ | 28 |
| 56 |
Then, repeat the process.
| $\frac{1}{2}$ | 28 |
| $\frac{1}{2}$ | 56 |
| ? |
56 ÷ $\frac{1}{2}$ → 56 × $\frac{2}{1}$ → 112
| $\frac{1}{2}$ | 28 |
| $\frac{1}{2}$ | 56 |
| 112 |
So,
28=$\frac{1}{2}$ ×$\frac{1}{2}$ x 112
28=$\frac{1}{4}$ ×112
| $\frac{1}{2}$ | 28 |
| $\frac{1}{2}$ | 56 |
| $\frac{1}{2}$ | 112 |
| ? |
1112 ÷ $\frac{1}{2}$ → 112 × $\frac{2}{2}$ → 224
| $\frac{1}{2}$ | 28 |
| $\frac{1}{2}$ | 56 |
| $\frac{1}{2}$ | 112 |
| 224 |
So,
28=$\frac{1}{2}$ ×$\frac{1}{2}$ x $\frac{1}{2}$ ×224
28=$\frac{1}{8}$×224
Scraping all the information we got, we can get a product of 28 with the pairs of factors of ($\frac{1}{2}$, 56), ($\frac{1}{4}$, 112), and ($\frac{1}{8}$, 224). You may notice that 224 can still be divided by $\frac{1}{2}$. That proves that we can an have infinite number of factors that are in fractions. So the first three we listed are the basic pairs of factors having a fraction for each one of them.
But we can also have a pair of factors that are both fractions. We can obtain them by finding first the pair of factors that are lower than 28. To do that, let us divide 28 into 8 parts.
28
| $\frac{7}{2}$ | 7 | $\frac{21}{2}$ | 14 | $\frac{35}{2}$ | 21 | $\frac{49}{2}$ | 28 |
| ↑$\frac{1}{8}$ | ↑$\frac{1}{4}$ | ↑$\frac{3}{8}$ | ↑$\frac{1}{2}$ | ↑$\frac{5}{8}$ | ↑$\frac{3}{4}$ | ↑$\frac{7}{8}$ | ↑1 |
Then, let us choose a pair above that are both fractions and if one of the pairs is a whole number, its partner factor must not have a numerator of 1.
From the illustration above, we can choose $\frac{7}{2}$ and $\frac{1}{8}$, $\frac{21}{2}$ and $\frac{3}{8}$, $\frac{35}{2}$ and $\frac{5}{8}$, 21 and $\frac{3}{4}$, and $\frac{49}{2}$ and $\frac{7}{8}$. But be careful by not declaring $\frac{7}{2}$ and $\frac{1}{8}$ as factors of 28 right away for instance because it will give an incorrect product. Instead, we are going to reciprocate $\frac{1}{8}$ before multiplying it by $\frac{7}{2}$ to get a product of 28.
$\frac{7}{2}$ and $\frac{1}{8}$
$\frac{1}{8}$ reciprocal 8
$\frac{7}{2}$ ×8 ? = 28
$\frac{56}{2}$ ? = 28
28 ✔ = 28
28=($\frac{7}{2}$, 8)
$\frac{21}{2}$ and $\frac{3}{8}$
$\frac{3}{8}$ reciprocal $\frac{8}{3}$
$\frac{21}{2}$ ×$\frac{8}{3}$ ? = 28
$\frac{168}{6}$ ? = 28
28 ✔ = 28
28=($\frac{21}{2}$ ,$\frac{8}{3}$)
$\frac{35}{2}$ and $\frac{5}{8}$
$\frac{5}{8}$ reciprocal $\frac{8}{5}$
$\frac{35}{2}$ ×$\frac{8}{5}$ ? = 28
$\frac{280}{10}$ ? = 28
28 ✔ = 28
28=($\frac{35}{2}$ ,$\frac{8}{5}$)
21 and $\frac{3}{4}$
$\frac{3}{4}$ reciprocal $\frac{4}{3}$
21 ×$\frac{4}{3}$ ? = 28
$\frac{84}{3}$ ? = 28
28 ✔ = 28
28=(21, $\frac{4}{3}$)
$\frac{49}{2}$ and $\frac{7}{8}$
$\frac{7}{8}$ reciprocal $\frac{8}{7}$
$\frac{49}{2}$ ×$\frac{8}{7}$ ? = 28
$\frac{392}{14}$ ? = 28
28 ✔ = 28
28=($\frac{49}{2}$ ,$\frac{8}{7}$)
Gathering all of the information, we can get also a product of 40 having the pair of factors of $\frac{7}{2}$ and 8, $\frac{21}{2}$ and $\frac{8}{3}$, $\frac{35}{2}$ and $\frac{8}{5}$, 21 and $\frac{4}{3}$, and $\frac{49}{2}$ and $\frac{8}{7}$.
Furthermore, the basic pairs of factors of 28 that are both fractions are $\frac{21}{2}$ and $\frac{8}{3}$, $\frac{35}{2}$ and $\frac{8}{5}$, and $\frac{49}{2}$ and $\frac{8}{7}$.
Factors of 28 that are in Decimal Form
Fractions can also be in Decimal Form since they both express the inexactness of a number. So, to get the pair of factors of 28 that are in decimal form, we have to transform the factors that are fractions we derived earlier into decimal forms.
| 28 = ($\frac{1}{2}$, 56) | 28 = (0.5, 56) | ||
| 28 = ($\frac{1}{4}$, 112) | 28 = (0.25, 112) | ||
| 28 = ($\frac{1}{8}$, 224) | 28 = (0.125, 224) | ||
| 28=($\frac{7}{2}$, 8) | 28=(3.5, 8) | ||
| 28=($\frac{21}{2}$ ,$\frac{8}{3}$) | 28=(10.5 ,2.$\overline{6}$) | ||
| 28=($\frac{35}{2}$ ,$\frac{8}{5}$) | 28=(17.5 ,1.6) | ||
| 28=(21, $\frac{4}{3}$) | 28=(21, 1.$\overline{3}$) | ||
| 28=($\frac{49}{2}$ ,$\frac{8}{7}$) | 28=(24.5 ,1.14…) |
To interpret the data above, we can also get a product of 28 having the factors of 0.5 and 56, 0.25 and 112, 0.125 and 224, 3.5 and 8, 10.5 and 2.$\overline{6}$, 17.5 and 1.6, 21 and 1.$\overline{3}$, and 24.5 and 1.14…
Group Factors of 28
By definition, factors, even though usually are in pairs can also come in groups. With this in mind, the combination of the factors is infinite but the way how to obtain them is having the principle we got from the prime factorization.
28 = 2 x 2 x 7
We can see from the prime factorization of 28 that we can have more than 2 number of factors to get a product. The same thing goes with other groups of factors that have a product of 28. To explore the possible group of factors of 28, let us have some examples by finding the missing factor in each group of factors of 28.
Example 1:
28 = -2 x 14 x ?
Solution:
First, multiply the given factors.
28 = -2 x 14 x ?
28 = -28 x ?
Then, divide 28 by the product obtained to get the missing factor.
28 ÷ -28 = -1
So, the missing factor is -1. This means that we can get 28 by having the factors of -2, 14, and -1.
28 = -2 x 14 x -1
28 = (-2, 14, -1)
Example 2:
28 = 0.25 x 0.5 x ?
Solution:
First, multiply the given factors.
28 = 0.25 x 0.5 x ?
28 = 0.125 x ?
Then, divide 28 by 0.125 to get the missing factor.
28 ÷ 0.125 = 224
Thus, the missing factor is 224. This means that we can get 28 by having the factors of 0.25, 0.5, and 224.
28 = 0.25 x 0.5 x 224
28 = (0.25, 0.5, 224)
The Differences between the Factors of 28 and Multiples of 28
Now that we know the Factors of 28, we can now distinguish this concept from the Multiples of 28. Let us have an illustration of the Factors of 28 and the Multiples of 28 to see their differences.
factors of 28 1×28 x y 1×28
x y =28 multiples of 28 ↓ =28
2×14 =28 2×28 =56
4×7 =28 3×28 =84
4×28 =112
5×28 =140
From the illustration above, it is apparent that the factors of 28 are numbers needed to be multiplied to obtain the same product (i.e. 28). On the other hand, the multiples of 28 are products obtained from multiplying 28 by 1 and so on. So, be careful not to interchange the terms because they are different from any angle.
Key Factors and Summary
- Factors of 28 are pairs or groups of numbers needed to multiply to obtain a product of 28.
- To list the factors of 28, we can use various strategies to get its pairs of factors, namely:
- Prime Factorization Using Factor Tree and Tabular Division
- Using the Rules of Divisibility
- The total amount of the positive integer factors of 28 is 6, namely: 1, 2, 4, 7, 14, and 28.
- By excluding 2, we have 5 proper factors of 28: 1, 2, 4, 7, and 14.
- The sum of the positive integer factors of 28 is 56, while the sum of the proper factors is 28 which makes it a perfect number (where a perfect number is equal to the sum of its proper factors.
- By definition, we can also have factors of 28 that come in negative integers, fractions, and decimals. Aside from being paired, we can also have factors of 28 that come in groups.
- Factors of 28 are pairs or groups of numbers needed to be multiplied to derive a product of 40, while the Multiples of 40 are products that can be obtained by multiplying 40 by 1 and so on.
Recommended Worksheets
Factors and Multiples (Ages 8-10) Worksheets (Space themed)
Understanding Factors and Multiples 4th Grade Math Worksheets
Finding Common Factors Between Two Whole Numbers Within 100 6th Grade Math Worksheets









