Factors of 18

Introduction

In mathematics, we are often faced with the challenge of solving problems that require divisibility of integer numbers and easy recognition of integers into which a number is divisible by integer. Such numbers are called factors and the main purpose of this article is to determine which numbers are divisors of 18 and which are not, to determine whether the factors of an integer, for example for number 18, can be fractional and negative numbers.  

Definition of factors

The factor of a number is the number that divides evenly the given number. Usually when we talk about number factors, we only talk about positive whole factors.

For example, the factors of 6 are 1, 2, 3 and 6. If 6 is divided by any of the numbers 1, 2, 3, 6, the answer will be a whole number:

6÷1=6

6÷2=3

63=2

66=1

The factors of a number are any numbers that divide into it exactly, including 1 and the number itself. Number 1 is always the smallest whole factor of the number, the number itself is always the greatest whole factor of the number. So, each number always has at least two factors.

If a number has exactly two factors, 1 and the number itself, this number is called a prime number. Number 1 is not a prime number. The smallest prime number is number 2 (is evenly divisible by 1 and by 2). To determine whether a number is prime or not, you can search for this number in the table of prime numbers. 

Table of prime numbers up to 1,000

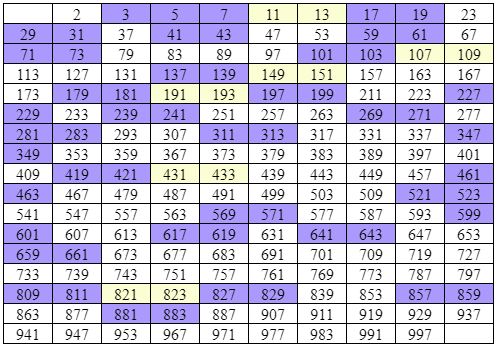
INTERESTING FACT: Two consecutive prime numbers are called twin numbers or twins. All twins from 2 to 1,000 are marked in the table above.

EXAMPLE: Which of the following numbers are prime?

117, 191, 227, 319, 473, 502

SOLUTION: If you need easily and quickly determine whether a number is prime or not, use the table of prime numbers.

Search for number 117 – there are numbers 113 and 127, but there is no number 117. This means number 117 is not a prime number.

Search for number 191 – this number is in the table, so this number is a prime number.

Among numbers 227, 319, 473, 502, only number 227 is in the table of prime numbers, so only this number is a prime number. 

By the way, you can easily state that the number 502 is not a prime number – this number is evenly divisible by 2, so it is even number and even number greater than 2 can never be prime number.

A number that has more than two factors is called a composite number. 

Ways of finding factors of a number

There are three methods of finding factors of a number:

• division method;
• multiplication method;
• prime factorization method.

DIVISION METHOD: the division method is to find all divisors from 1 to the number itself that divide the number without remainder.

MULTIPLICATION METHOD: the multiplication method is to write the number as a product of two numbers in different possible ways.

PRIME FACTORIZATION METHOD: the prime factorization method is to express a composite number as the product of its prime factors.

Division method of finding the factors of 18

Since number 18 is not in the table of prime numbers, number 18 is a composite number, so it has more than two factors.

We can use division to find all positive factors of 18 (start with 1, then check 2, 3, 4, 5, 6 etc. up to 9 (number 9 is exactly half of 18) and the number 18 itself):

18÷1=18

18÷2=9

18÷3=6

18÷4=4 r.2

18÷5=3 r.3

18÷6=3

18÷7=2 r.4

18÷8=2 r.2

18÷9=2

1818=1

Therefore, 18 has a total of 6 positive factors: 1, 2, 3, 6, 9 and 18.

Multiplication method of finding the factors of 18

Represent the number 18 as a product of two numbers in all different possible ways:

18= 1 × 18

18= 2 ×  9

18= 3 ×  6

All the numbers that are used in these products are the factors of 18. Thus, the positive factors of 18 are 1, 2, 3, 6, 9 and 18.

Prime factorization method of finding the factors of 18

Prime factorization is a way of expressing a number as a product of its prime factors. For example,

18=6×3

is not the prime factorization of 18 as number 6 is not a prime number.

The product 

18=2×3×3

is the prime factorization of 18 as numbers 2 and 3 are prime numbers.

There are two possible ways to express number as a product of prime factors:

• division method;
• factor tree method.

PRIME FACTORIZATION USING DIVISION METHOD 

The division method can be used to find the prime factors of a number by dividing the number by prime numbers. To find the prime factors of a number using the division method complete the next steps:

STEP 1: Evenly divide the number by the smallest possible prime number.
STEP 2: Evenly divide the quotient of step 1 by the smallest possible prime number.
STEP 3: Repeat step 2, until the quotient becomes 1.
LAST STEP: Multiply all the prime factors that are the divisors.

EXAMPLE: Write the prime factorization of the number 18 using the division method.

SOLUTION: 

STEP 1: The smallest possible prime number that evenly divides 18 is number 2. Divide 18 by 2:

18 ÷ 2=9

STEP 2:  The smallest possible prime number that evenly divides the quotient 9 is number 3. Divide 9 by 3:

9 ÷ 3=3

STEP 3:  The smallest possible prime number that evenly divides the quotient 3 is number 3. Divide 3 by 3:

3 ÷ 3=1

LAST STEP: Multiply all the prime factors that are the divisors:

18=2×3×3

You can rewrite this prime factorization in the exponent form:

18=2 x 3²

REMARK: Usually this process is not described for so long, but depicted in the form of a column as shown below.

2	18
3	9
3	3
	1

Prime factorization of 18=2x3x3

                                          =2×3² 

PRIME FACTORIZATION USING FACTOR TREE METHOD 

A factor tree is a special diagram, where we draw the factors of a number, then the factors of those factors and so on until we get only prime factors. 

EXAMPLE: Draw a factor tree for the number 18.

SOLUTION: From the multiplication table we know that 18=9×2. Therefore,

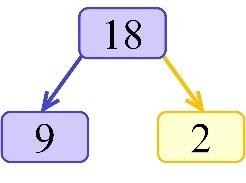
One of these numbers we can represent as products of prime numbers:

9=3×3

So, the final factor tree is 

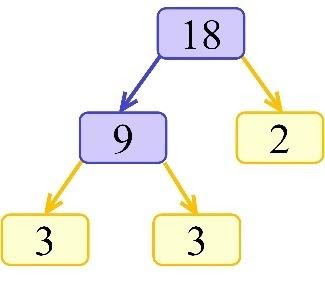
and the prime factorization of 18 is 2×3×3 or 2×3².

REMARK: You can start with arbitrary numbers giving 18 in product, but the final product must be always the same as the prime factorization is unique. For example, you can draw the following two factor trees for the number 18 and see that that the prime factorization for all factor trees are the same. This is provided by the Fundamental Theorem of Arithmetic which states that 

every natural number greater than 1 can be written as a product of prime numbers, and that up to rearrangement of the factors, this product is unique.

To find the prime factors of a number using the factor tree method complete the next steps:

STEP 1: Draw a factor tree starting from arbitrary numbers with product equal to the given number but finishing with only prime numbers.
STEP 2: Multiply all the prime factors that appear in this factor tree.

The method of finding the factors of a number using the prime factorization of the number is to multiply arbitrary combinations of prime factors. 

EXAMPLE: The prime factorization of 18 is 2 x 3². Write down all positive factors of 18 using the prime factorization method.

SOLUTION: To write down all the factors and not lose any, use the following guidance of writing combinations:

• first, write down all possible powers of the first prime factor (starting with exponent of 0 and finishing with the maximum possible exponent defined in the prime factorization of the number):

2⁰=1, 2¹=2

• then write down all possible powers of the second prime factor (starting with exponent of 0 and finishing with the maximum possible exponent defined in the prime factorization of the number):

3⁰=1, 3¹=3, 3²=9

• and then all possible products of powers of both multipliers

2¹ x 3¹=6, 2¹ x 3²=18,

Therefore, the list of all 6 positive factors of 18 written in ascending order is  

1, 2, 3, 6, 9, 18

Note that only 2 and 3 are prime factors of 18.

Finding the number of positive factors

Using the prime factorization of a number, we can find the number of factors of this number. To do this, complete the following steps:

STEP 1: Write the prime factorization of a number in the exponent form.
STEP 2: Add one to each of the exponents.
STEP 3: Multiply all obtained numbers. This product denotes the number of factors of a number.

EXAMPLE: Find the number of factors of 18.

SOLUTION: From the previous topic, the prime factorization of the number 18 in the exponent form is 2 x 3².

Add 1 to each exponent:

1+1=2

2+1=3

and multiply the obtained sums:

2×3=6

Therefore, the number of factors of 18 is 6.

Positive factor pairs of 18

A factor pair of a number is a set of two factors, which, when multiplied, give this number as a product. For example, factors 5 and 6 form a factor pair of 30 because 

30=5×6

EXAMPLE: List all factor pairs of 18.

SOLUTION: Start with 1. Since 18=1×18, put 1 at the beginning of the list and 18 at the end of the list. Factors 1 and 18 form the first factor pair of 18.

1

18

Now, try 2. Since 18=2×9, put 2 at the beginning of the list (after 1) and 9 at the end of the list (before 18). Factors 2 and 9 form the second factor pair of 18.

1

2

9

18

Then, try 3. Since 18=3×6, put 3 at the beginning of the list (after 2) and 6 at the end of the list (before 9). Factors 3 and 6 form the third factor pair of 18.

1

2

3

6

9

18

There are no more whole factors of 18 between 3 and 6 so we are done!

We can graphically represent positive factor pairs as shown below.

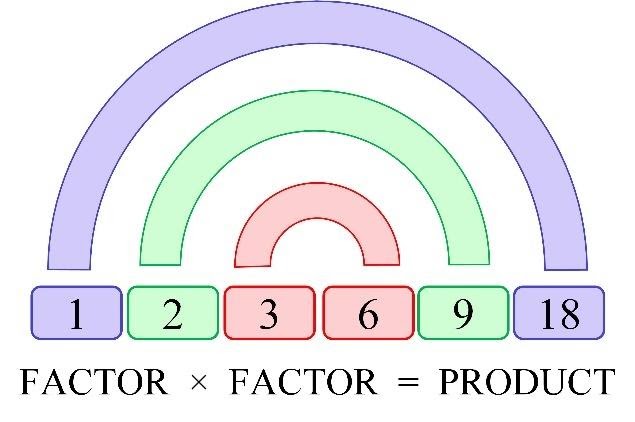
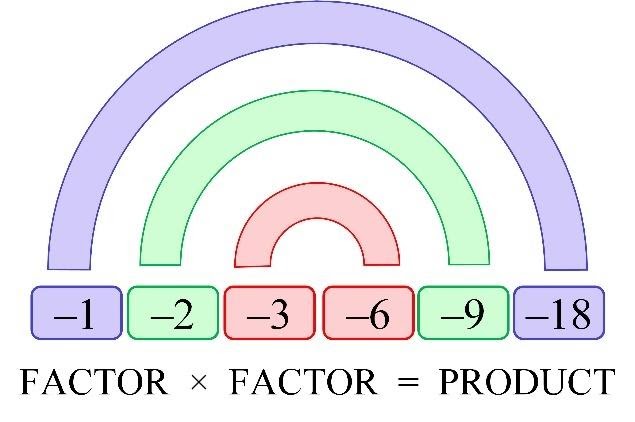
Negative factors of 18

From the previous topic you can see that there are 3 factor pairs of 18. All these pairs consist of positive whole numbers. 

If we note that the product of two negative numbers gives a positive number, then the same pairs of negative numbers will also be factor pairs. 

Therefore, negative factor pairs are 

-1 and -18

-2 and -9

-3 and -6

and list of negative factor pairs is 

-1

-2

-3

-6

-9

-18

Here two numbers colored in one color form a negative factor pair.

Also, we can graphically represent negative factor pairs in the same way as graphical representation of positive factor pairs.

Quiz

1. What is the sum of all positive factors of 18?

SOLUTION: Number 18 has 6 positive factors: 1, 2, 3, 6, 9 and 18. The sum of these factors is 1+2+3+6+9+18=39.

ANSWER: 39

2. How many factor pairs does the number 18 have?

SOLUTION: Number 18 has 3 positive factor pairs: 

(1, 18), (2, 9) and (3, 6)

and 3 positive factor pairs: 

(-1, -18), (-2, -9) and (-3, -6)

Thus, there are 6 factor pairs for number 18.

ANSWER: 6

3. The area of the rectangle is 18 un². If the length and the width of the rectangle are whole numbers, how many different perimeters can this rectangle have? What are the numerical values of these perimeters?

SOLUTION: The area of the rectangle can be found by multiplying the width of the rectangle by its length. If the length and the width of the rectangle are whole numbers, then there are three possibilities:

Width	Length
1 un.	18 un.
2 un.	9 un.
3 un.	6 un.

Note that we are interested in different pairs of widths and lengths that is a pair with the width of 1 un. and length of 18 un. specifies the same rectangle as a pair with the width of 18 un. and length of 1 un.

The perimeter of the rectangle is the doubled sum of its width and length. Fill in the following table to find the perimeter of the rectangle in each case:

Width	Length	Perimeter
1 un.	18 un.	2(1+18)=28 un.
2 un.	9 un.	2(2+9)=22 un.
3 un.	6 un.	2(3+6)=18 un.

ANSWER: 3 different perimeters: 38 un., 22 un. and 18 un. 

4. Which of the following statements is true?

a) Number 18 is a prime number.

b) Number 18 is a composite number.

c) Number -9 is a factor of 18.

d) Number 180 is a factor of 18 because 180⋅$\frac{1}{10}$=18.

SOLUTION: a) Number 18 is between 17 and 19. Numbers 17 and 19 are in the table of prime numbers and number 18 is not in the table of prime numbers. This means number 18 is not a prime number and statement a) is false.

b) Since number 18 is not in the table of prime numbers, this number is a composite number and statement b) is true. 

c) Looking at negative factor pairs, we see that (-2, -9) is a negative factor pair of 18. This means number -9 is a factor of 18 and statement c) is true.

d) Number 180 is not a factor of 18 because the equality 180⋅110=18 contains fractional numbers which cannot be factors. So, statement d) is false.

ANSWER: a) False 

b) True

c) True

d) False

5. CHALLENGE QUESTION: If you know factors of 18, how can you find positive factors of 18²? If number 18 has 6 positive factors, can you tell how many positive factors does number 18² have?

SOLUTION: From the article, the prime factorization of 18 is 2×3². Then, 

18²=(2×3²)²=2² x 3⁴

This helps us to find the number of factors of 18² and the list of these factors.

To find the number of factors, add 1 to each exponent:

2+1=3

4+1=5

and multiply the obtained sums:

3 x 5=15

Therefore, the number of factors of 18² is 15.

Now, use the algorithm from the example in the article to find all factors of 18². 

• first, write down all possible powers of the first prime factor (starting with exponent of 0 and finishing with the maximum possible exponent defined in the prime factorization of the number):

2⁰=1, 2¹=2, 2²=4

• then write down all possible powers of the second prime factor (starting with exponent of 0 and finishing with the maximum possible exponent defined in the prime factorization of the number):

3⁰=1, 3¹=3, 3²=9, 3³=27, 3⁴=81

• and then all possible products of powers of both multipliers

2¹x3¹=6, 2¹x3²=18, 2¹x3³=54, 2¹x3⁴=162,

2²x3¹=12, 2²x3²=36, 2²x3³=108, 2²x3⁴=324

Therefore, the list of all 15 positive factors of 182=324 written in ascending order is  

1, 2, 3, 4, 6, 9, 12, 18, 27, 36, 54, 81, 108, 162, 324

ANSWER: 15 positive factors: 1, 2, 3, 4, 6, 9, 12, 18, 27, 36, 54, 81, 108, 162, 324

Conclusions

1. Number 18 is composite number (it has more than two factors).
2. Number 18 has 6 positive factors: 1, 2, 3, 6, 9, 18 and 6 negative factors: -1, -2, -3, -6, -9, -18.
3. 6 positive factors of 18 form 3 factor pairs as well as 6 negative factors.
4. There are only 3 different factor trees of number 18.

Recommended Worksheets

Factors and Multiples (Ages 8-10) Worksheets (Space themed)
Multiplying Fractions with Whole Numbers with Word Problems (with denominators from 2 to 6) 4th Grade Math Worksheets
GCF: Greatest Common Factor (Valentine’s Day Themed) Math Worksheets