Introduction
Factoring Difference of Two Squares (DOTS) is a crucial technique in the realm of algebra that simplifies expressions and solves equations. With a solid understanding of this method, one can efficiently tackle various mathematical problems, especially at higher levels of algebra and calculus.
This article delves into the definition, key steps, method, examples, and questions related to factoring DOTS, ultimately providing a comprehensive understanding of this essential skill.
Required Knowledge
Students should already be familiar with expanding expressions that result in a difference of two squares, factoring perfect square expressions, and square roots of perfect squares and rational numbers.
Grade Appropriateness
Factoring difference of two squares is typically taught to learners aged 11-13 years old or 7th to 8th grades.
Definition
The Difference of Two Squares (DOTS) refers to a mathematical expression as a² – b², where a and b represent numbers or algebraic expressions, and the square ( 2 ) denotes the power to which they are raised.
Factoring DOTS is breaking mathematical expressions into simpler components using a unique algebraic identity.
Identity and Key Steps
The fundamental identity used for factoring DOTS is:
a² – b² = ( a + b )( a – b )
This identity states that the difference of two squares can be factored into two binomial expressions, (a + b) and (a – b). The key steps in factoring DOTS are:
- Identify the expression in the form of a² – b².
- Determine the values of a and b.
- Apply the DOTS identity by substituting the values of a and b into (a + b)(a – b).
Methods
Let’s delve deeper into the factoring method with a step-by-step breakdown:
Step 1: Identify the expression in the form of a² – b².
Ensure that the given expression has two terms and is in the form of a² – b². If not, try simplifying the expression or rearranging the terms to achieve this form.
Step 2: Determine the values of a and b.
Find the square roots of the first term (a²) and the second term (b²), represented by a and b, respectively.
Step 3: Apply the DOTS identity.
Substitute the values of a and b into the DOTS identity, (a + b)(a – b), to obtain the factored form of the expression.
Examples
Let’s apply the method to some examples:
Example 1
Factor the expression: 16x² – 81y².
- Identify the expression: 16x² – 81y²
- Determine the values of a and b:
a = 4x, since (4x)² = 16x² or $\sqrt(16x^2)$ = 4x
b = 9y, since (9y)² = 81y² or $\sqrt(81x^2)$ = 9y
- Apply the DOTS identity: (4x + 9y)(4x – 9y)
Hence, the factored form of the expression 16x² – 81y² is (4x + 9y)(4x – 9y).
Example 2:
Factor the expression: 25a² – 1.
- Identify the expression: 25a² – 1
- Determine the values of a and b:
a = 5a, since (5a)² = 25a² or $\sqrt(25a^2)$ = 5a
b = 1, since (1)² = 1 or $\sqrt(1)$ = 1
- Apply the DOTS identity: ( 5a + 1 )( 5a – 1 )
Hence, the factored form of the expression 25a² – 1 is (5a + 1)(5a – 1).
Example 3
Factor the expression: 16-4x².
- Identify the expression: 16-4x²
- Determine the values of a and b:
a = 4, since 4² = 16 or $\sqrt(16)$ = 4
b = 2x, since (4x)² = 2x or $4x^2$ = 2x
- Apply the DOTS identity: ( 4+2x )( 4 – 2x ).
Hence, the factored form of the expression -4x² + 16 is (4 + 2x)(4 – 2x).
Practice Test
To enhance your understanding and practice factoring DOTS, try solving the following expressions:
- 49m² – 64n²
- x² – 100
- 4y²- 9z²
- 81p² – 16q²
- 121r2- 36s²
Solutions:
1. 49m² – 64n²
Identify the expression: 49m² – 64n²
Determine the values of a and b:
a = 7m, since (7m)² = 49m² and
b = 8n, since (8n)² = 64n²
Apply the DOTS identity: (7m + 8n)(7m – 8n)
Therefore, the factored form of the expression 49m² – 64n² is (7m + 8n)(7m – 8n).
2. x² – 100
Identify the expression: x² – 100
Determine the values of a and b:
a = x, since $\sqrt(x^2)$ = x
b = 10, since $\sqrt(100)$ = 10
Apply the DOTS identity: (x + 10)(x – 10)
Hence, the factored form of x² – 100 is (x + 10)(x – 10).
3. 4y² – 9z²
Identify the expression: 4y² – 9z²
Determine the values of a and b:
a = 2y, since (2y)² = 4y² and
b = 3z, since (3z)² = 9z²
Apply the DOTS identity: (2y + 3z)(2y – 3z)
Hence, the factored form of 4y² – 9z² is (2y + 3z)(2y – 3z).
4. 81p² – 16q²
Identify the expression: 81p² – 16q²
Determine the values of a and b:
a = 9p, since (9p)² = 81p² and
b = 4q, since (4q)² = 16q²
Apply the DOTS identity: (9p + 4q)(9p – 4q)
Hence, the factored form of the expression is (9p + 4q)(9p – 4q).
5. 121r² – 36s²
Identify the expression: 121r² – 36s²
Determine the values of a and b:
a = 11r, since ( 11r )² = 121r² or $\sqrt(121r^2)$ = 11r
b = 6s, since (6s)² = 36s² or $\sqrt(36s^2)$ = 6s
Apply the DOTS identity: (11r – 6s)(11r – 6s)
Hence, the factored form of 121r² – 36s² is (11r+6s)(11r – 6s).
Real-life Application
Erica must grow flowers on the square garden lot shown in the diagram below. She had already begun planting flowers in the garden. Determine the area of the remaining space where she needs to plant flowers.
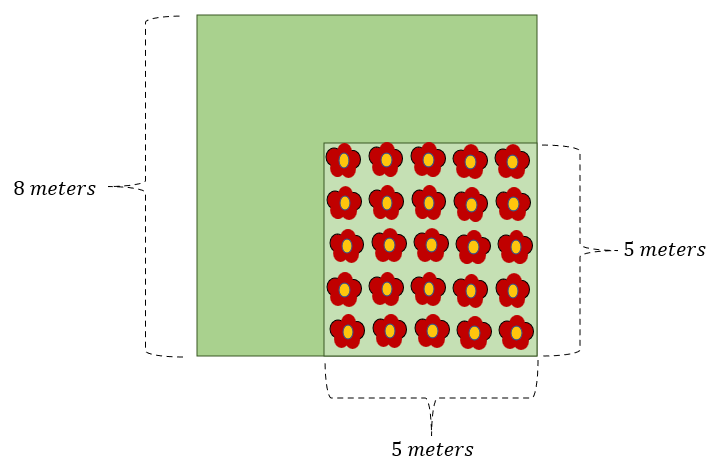
Solution
This problem may be solved using the difference of squares identity a² – b² = ( a + b )( a – b ).
Since we want to find the area of the space without flowers, we must subtract the area of the square space with flowers from the total area of the square lot.
So, we have,
Area of the square garden lot = 8²
Area of garden lot planted with flowers = 5²
Applying factoring DOTS, we will have,
8² – 5² = ( 8 + 5 )( 8 – 5 )
8² – 5² = (13)(3)
8² – 5² = 39
Therefore, the area of the remaining space that Erica needs to plant flowers is 39 m².
Conclusion
Factoring Difference of Two Squares (DOTS) is an essential algebraic technique that simplifies complex expressions and eases the process of solving equations. By mastering the method and practicing with various examples, one can improve their problem-solving skills and succeed in higher-level mathematics.
Frequently Asked Questions (FAQs)
What are the steps in factoring the difference of two squares?
In factoring the difference of two squares, we follow the following steps:
Step 1: Identify the expression in the form of a² – b².
Step 2: Determine the values of a and b by getting the square root of a² and b².
Step 3: Apply the DOTS identity, ( a + b )( a – b ).
Let us say we want to factorize 25x² – 36y².
Step 1: Identify the expression in the form of a² – b².
a² = 25x² and b² = 36y²
Step 2: Determine the values of a and b.
a=5x, since ( 5x )²2 = 25x² or $\sqrt(25x^2)$ = 5x
b=6y, since 6y² = 36y² or $\sqrt(36y^2)$ = 6y
Step 3: Apply the DOTS identity.
( 5x + 6y )( 5x – 6y )
Therefore, the factored form of 25x² – 36y² is ( 5x + 6y )( 5x – 6y ).
What is the formula for the difference of two squares?
The fundamental identity used for factoring DOTS is:
a² – b² = (a + b)(a – b)
This identity states that the difference of two squares can be factored into two binomial expressions, (a + b) and (a – b).
Other ways to express the difference of two squares formula using variables include the following examples:
x² – y² = (x+y) (x-y)
m² – n² = (m+n) (m-n)
When can we factor a mathematical expression using the difference of two squares?
When the terms of a binomial are perfect squares, and the operation involved is subtraction, then we are guaranteed the case of the difference of two squares.
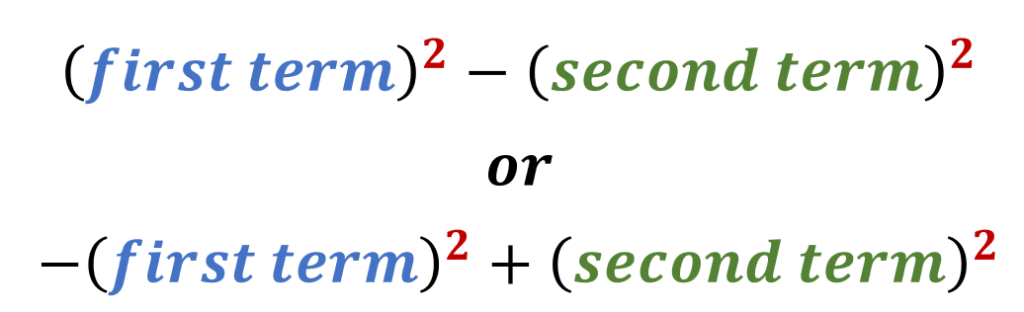
How do you evaluate the difference of two squares?
We will use the formula of the difference of two squares a² – b² = ( a + b )( a – b ).
Let us say; for example, we must evaluate ( 15 )² – ( 10 )².
Since the given expression is in the form a² – b², we know that a=15 and b=10.
Applying the formula, we’ll have,
( 15 )² – ( 10 )² = ( 15+10 )( 15-10 )
( 15 )² – ( 10 )² = ( 25 )( 5 )
( 15 )² – ( 10 )² = 125









