Home » Math Theory » Factors » Factors in Math

Factors in Math

Introduction

Multiplication and division are two of the important operations in mathematics. We can multiply a number by any number. Similarly, a number can be divided by any number. Two important terms that are related to the multiplication and division of numbers are factors and multiples. The understanding of one of these is incomplete without studying the other. Therefore, before we move ahead and learn about factors, let us recall what we mean by multiple of a number. 

What is a multiple?

A multiple of a whole number is the product of the number and any counting number. If we multiply 3 by 1, 2 , 3 , 4, 5 , 6 ….. we get

3 x 1 = 3

3 x 2 = 6

3 x 3 = 9

3 x 4 = 12

3 x 5 = 15

3 x 6 = 18 etc.

Thus 3, 6 , 9 , 12 , 15 , 18  and so on are the multiples of 3.

Now, let us understand the definition of factors.

Definition

A factor of a number is an exact divisor of that number. In other words, a factor of a number is that number that completely divides the number without leaving a remainder. For example, each of the numbers, 1, 2, 3, 4, 6 and 12 is a factor of 12. However, none of the numbers 5, 7, 8, 9, 10 and 11 is a factor of 12. 

Properties of Factors

Following are the properties of factors of a number – 

  1. 1 is a factor of every number. For example, 1 x 1 = 1, 4 x 1 = 4, 7 x 1 = 7 and so on
  2. Every number is a factor of itself. For example, we can write 6 as 6 x 1 = 6 which means that both 6 and 1 are the factor of the number 6. Similarly, we can write 12 as 12 x 1 = 12 which means that both 12 and 1 are the factor of the number 12.
  3. Every factor of a number is an exact divisor of the number itself. For example, the factors of the number 12 are 1, 2, 3, 4, 6 and 12. We can see that each of these factors divides 12. We can check the same for other numbers as well.
  4. Every factor of a number is less than or equal to that number. For example, if we consider the factors of 18, we will have, 1, 2, 3, 6, 9 and 18. Out of these numbers, 18 itself is the largest factor and all other factors are less than 18.
  5. Factors of a given number are finite. We have seen in the previous property that the factors are 18 are 1, 2, 3, 6, 9 and 18 and there cannot be a factor that is greater than the number 18 itself. Since the number is finite, therefore, it will have finite numbers of factors only.

Can we specify a name to a number that has no other factor other than 1 and the number itself? 

Factors and Types of Numbers

We can define different types of numbers based on the number of factors of a number. Some such types of numbers are – 

  1. Prime Numbers
  2. Composite Numbers
  3. Co-Prime Numbers

Prime Numbers

A number having only two factors is called a prime number. The two factors are the number 1 and the number itself. For example, consider the number 7. The number 7 has only factors, 1 and the number 7 itself. Therefore, 7 is a prime number. Similarly, the number 11 is also a prime number as it has only two factors, 1 and the number 11 itself. 

Composite Numbers

A number that has more than two factors is called a composite number. Examples of composite numbers are 4, 6, 8 and 9.

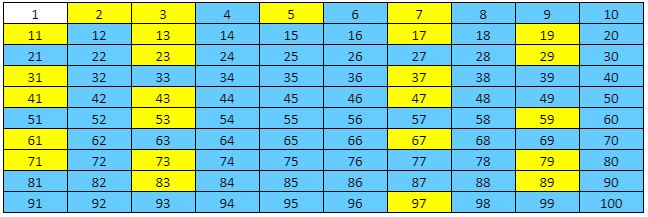
Prime and Composite Numbers Chart

In the following chart, the numbers highlighted in yellow are composite numbers while the numbers highlighted in blue are prime numbers. As stated above, 1 is neither prime nor composite.

Number Patterns of Prime and Composite Numbers

Co-Prime Numbers

Co-Prime numbers are the numbers that have no common factor apart from 1. Co-prime numbers are different from prime numbers. While prime numbers are all odd numbers with the only exception being 2 which is an even number, the co-prime numbers can be both prime and composite with the only condition being that they have no other factor other than 1. Let us consider some examples to understand it better.

Suppose we have two numbers 5 and 7.

Now we can see that the numbers 5 and 7 are both prime numbers. Since they both are prime numbers, we can say that – 

5 = 5 x 1

7 = 7 x 1 

From above, it is clear that both 5 and 7 have no common factors between them other than 1. Hence, we can say that the numbers 5 and 7 are co-prime numbers.

Thus a pair of numbers can both be prime numbers as well as co-prime numbers.

Common Factors

We have now learnt about the factors as well as multiples of a number. Let us now look at the factors of more than one number. Those factors which are common among the factors of two or more numbers are known as common factors. Let us understand it through an example.

Let us consider two numbers, 12 and 18. The factors of 12 and 18 are – 

Factors of 12 are – 1, 2, 3, 4, 6 and 12

Factors of 18 are – 1, 2, 3, 6, 9 and 18.

From above, we can clearly see that 1, 2, 3 and 6 are the common factors of 12 and 18.

Let us consider another example.

Consider the numbers 9, 15 and 21. The factors of 9, 15 and 21 are – 

Factors of 9 – 1, 3 and 9

Factors of 15 – 1, 3, 5 and 15

Factors of 21 – 1, 3, 7 and 21

From above, we can clearly see that 1 and 3 are the common factors of 9, 15 and 21.

Now, that we have understood how to find common factors between numbers, it is clearly understood that there would always be one largest factor among all the common factors. Can we assign a name to this largest factor? Let us find out.  

Highest Common Factor ( H. C. F. )

We now know how to compare factors of two or more numbers. We can also find out the largest factor among these common factors so obtained. For example, we found that the common factors of 9, 15 and 21 are 1, 3, 7 and 21. Out of these 21 is the highest common factor or H.C.F. So, how do we define the highest common factor?

The highest common factor ( H. C. F. ) of two or more numbers is the greatest or the largest among common factors. In other words, the H. C. F. of two or more numbers is the largest number that divides all the given numbers exactly. 

Now let us learn how to find the highest common factor ( H. C. F. ) of two or more numbers.

Finding H. C. F of Two Numbers

There are two ways of finding the highest common factor ( H. C. F. ) or two or more numbers. These methods are – 

  1. Prime Factorisation method
  2. Continued Division Method

Let us learn about them one by one.

Prime Factorisation method

In order to find the highest common factor ( H. C. F. ) of two or more numbers, the following steps are followed- 

  1. Obtain the numbers. 
  2. Write the prime factorisation of all the numbers.
  3. Identify the common factors.
  4. For each common prime factor find the minimum number of times it occurs in the prime factorisation of the given numbers.
  5. Multiply each common prime factor the number of times determine the previous step and find their product to get the highest common factor ( H. C. F. ) of the given numbers. 

Let us understand the above steps through an example.

Suppose we want to find the highest common factor ( H. C. F. ) of 90 and 48. We shall follow the above listed steps for this purpose.

  1. Obtain the numbers. We have the numbers as 90 and 48.
  2. Write the prime factorisation of all the numbers. We have,

90 = 2 x 3 x 3 x 5 and 48 = 2 x 2 x 2 x 2 x 3

  1. Identify the common factors. We can see from above that the common factors of 90 and 48 are 2 and 3.
  2. For each common prime factor find the minimum number of times it occurs in the prime factorisation of the given numbers. We can see that the common factor 2 appears one time in the prime factorisation of 90 while it appears 4 times in the prime factorisation of 48. Similarly, the common factor 3 appears two times in the prime factorisation of 48 while it appears one time in the prime factorisation of 48.
  3. Multiply each common prime factor the number of times determine the previous step and find their product to get the highest common factor ( H. C. F. ) of the given numbers. H. C. F. of 90 and 48 = 2 x 3 = 6

Continued Division Method

Euclid, a Greek mathematician devised an interesting method to find the H. C. F. of two or more numbers. This method is known as the continued division method or the Euclid algorithm. Following are the steps involve for finding the H. C. F. of two numbers using the continued division method – 

  1. Obtain the numbers and identify the greater number.
  2. Take the greater number as a dividend and the smaller number as the divisor. 
  3. Find the quotient and the remainder.
  4. If the remainder is zero, then the divisor is the H. C. F. else go to the next step.
  5. Take the remainder as the new divisor and the divisor as the new dividend.
  6. Repeat the steps 3, 4 and 5 till the remainder zero is obtained. The last divisor for which the remainder is zero is the required H. C. F. 

Let us understand the above steps through an example.

Example

Find the H. C. F. of the numbers 513 and 783

Solution

We have been given the numbers 513 and 783 and we need to find their H. C. F. Let us perform the above stated steps. We shall have, 

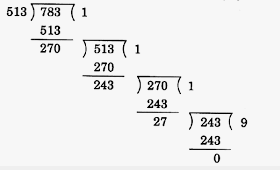
We can see that clearly, the last divisor is 27. Hence, the H. C. F. of the given numbers is 27.

H.C.F of more than two numbers

In order to find the H. C. F of more than two numbers, we proceed as follows – 

  1. Obtain the numbers and choose two numbers to start with and identify the greater number among them.
  2. Take the greater number as a dividend and the smaller number as the divisor. 
  3. Find the quotient and the remainder.
  4. If the remainder is zero, then the divisor is the H. C. F. else go to the next step.
  5. Take the remainder as the new divisor and the divisor as the new dividend.
  6. Repeat the steps 3, 4 and 5 till the remainder zero is obtained. The last divisor for which the remainder is zero is the required H. C. F. of these two numbers.
  7. Find the H. C. F. of the third number and H. C. F. obtained in the previous step.
  8. Take the H. C. F. obtained in the previous step as the required H. C. F. of three numbers.

Let us understand the above steps through an example.

Example

Find the H. C. F. of the numbers 144, 180 and 192

Solution

We have been given the numbers 144, 180 and 192 and we need to find their H. C. F. Let us perform the above stated steps. 

First let us find the H. C. F of 192 and 144

We can see that the H. C. F of 192 and 144 is 48.

Now, let us find the H. C. F of 48 and 180. We will have,

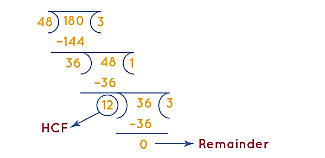
Now, we have obtained remainder as 0, we can see that the last divisor was 12. Hence, we can say that the H. C. F. of the numbers 144, 180 and 192 is 12.

Applications of H.C. F

Let us understand by an example areas where the highest common factor, H.C.F can be used in daily life.

Example

What is the largest number that divides 245 and 1029, leaving the remainder 5 in each case? 

Solution

It is given that the required number that divides 245 and 1029, leaving the remainder 5 in each case. This means that 

245 – 5 = 240 and 1029 – 5 = 1024 are completely divisible by the required number. It follows from this that the required number is a common factor of 240 and 1024. It is also given that the required number is the largest number satisfying the given property. therefore, the required number is the H.C.F of 240 and 1024. We will thus have,

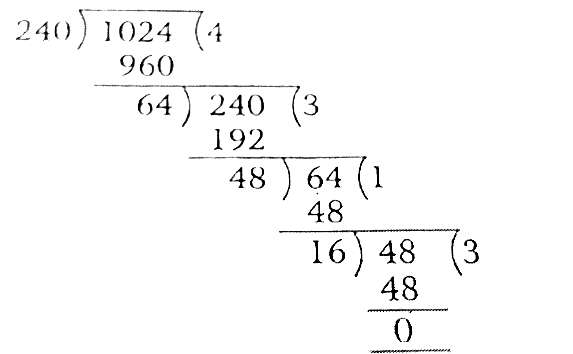
Clearly, the H.C.F of 240 and 1024 is 16. Hence, the required largest number that divides 245 and 1029, leaving the remainder 5 in each case is 16. 

Key Facts and Summary

  1. A multiple of a whole number is the product of the number and any counting number.
  2. A factor of a number is an exact divisor of that number.
  3. 1 is a factor of every number.
  4. Every number is a factor of itself.
  5. Every factor of a number is an exact divisor of the number itself.
  6. Every factor of a number is less than or equal to that number.
  7. Factors of a given number are finite.
  8. A number having only two factors is called a prime number. The two factors are the number 1 and the number itself.
  9. A number that has more than two factors is called a composite number. Examples of composite numbers are 4, 6, 8 and 9.
  10. Co – prime numbers are the numbers that have no common factor apart from 1. Co-prime numbers are different from prime numbers.
  11. The highest common factor ( H. C. F. ) of two or more numbers is the greatest or the largest among common factors. 
  12. There are two ways of finding the highest common factor ( H. C. F. ) or two or more numbers – Prime Factorisation method and Continued Division Method

GCF: Greatest Common Factor (Valentine’s Day Themed) Math Worksheets
Factors and Multiples (Ages 8-10) Worksheets (Space themed)
Understanding Factors and Multiples 4th Grade Math Worksheets

Browse All Worksheets

Link/Reference Us

We spend a lot of time researching and compiling the information on this site. If you find this useful in your research, please use the tool below to properly link to or reference Helping with Math as the source. We appreciate your support!

  • "Factors in Math". Helping with Math. Accessed on April 26, 2024. https://helpingwithmath.com/factors/.

  • "Factors in Math". Helping with Math, https://helpingwithmath.com/factors/. Accessed 26 April, 2024.

  • Factors in Math. Helping with Math. Retrieved from https://helpingwithmath.com/factors/.