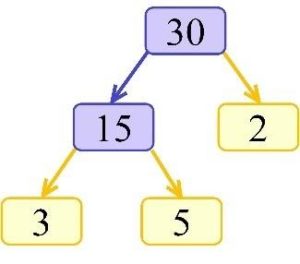
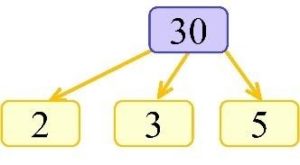
Introduction
Very often in the process of solving the problem we have questions that we do not have answers to at the moment. For example, is it possible to place 30 choir singers in several rows so that each row has the same number of singers and none one is left? This question is answered by the concept of factor.
Do you need to understand what a factor is and what are the factors of 30? You get to the right place at the right time and will get answers to your questions and much more!
Definition of factors
The factor of a number is the integer that divides evenly the given number. These numbers could be positive or negative whole numbers but mostly we talk about positive factors.
For example, the factors of 8 are 1, 2, 4 and 8. If 8 is divided by any of the numbers 1, 2, 4, 8, the answer will be a whole number:
8 ÷ 1=8
8 ÷ 2=4
8 ÷ 4=2
8 ÷ 8=1
In other words, factors of a number are basically the numbers that divide this number evenly or exactly without leaving any remainder. For example, if a number divides 30 with a remainder of 0, then that number is called a factor.
The factors of a number are any numbers that divide into it exactly, including 1 and the number itself. Number 1 is always the smallest whole factor of the number, the number itself is always the greatest whole factor of the number. So, each number always has at least two factors.
Prime numbers
If a number has exactly two factors, 1 and the number itself, this number is called a prime number. A number that has more than two factors is called a composite number.
- Whole number 1 is not a prime number – it has only one factor 1.
- The smallest prime number is number 2 (is evenly divisible by 1 and by 2).
- To determine whether a number is prime or composite, you need to check it with a table of prime numbers or using divisibility rules.
Divisibility rules
| Number | Divisibility rule | Evenly divisible Example | Not evenly divisible Example |
| 1 | Any integer (not a fraction) is divisible by 1 | 1, 2, 15, 100, … | – |
| 2 | The last digit is even (0, 2, 4, 6, 8) | 12, 100, 148,… | 5, 11, 27, … |
| 3 | The sum of the digits is divisible by 3 | 15, 36, 145, … | 7, 49, 115, … |
| 4 | The last two digits form a number divisible by 4 | 16, 128, 464, … | 39, 358, … |
| 5 | The last digit is 0 or 5 | 10, 45, 195,… | 34, 901, … |
| 6 | Is divisible by 2 and by 3 | 18, 42, 168, … | 45, 56, … |
| 7 | Double the last digit and subtract it from a number made by the other digits. The result must be divisible by 7 | 28, 147, … | 37, 109, … |
| 8 | The last three digits form a number divisible by 8 | 144, 2056, … | 242, 4102,… |
| 9 | The sum of the digits is divisible by 9 | 36, 378,… | 93, 805,… |
| 10 | Ends with 0 | 40, 800, 4050,… | 51, 208, … |
EXAMPLE: Check all divisibility rules from 1 to 10 for number 30.
SOLUTION: Check all divisibility rules by numbers from 1 to 10.
By 1: Number 30 is evenly divisible by 1 because any integer number is divisible by 1.
By 2: Number 30 is evenly divisible by 2 because it ends with even number 0.
By 3: Number 30 is evenly divisible by 3 because the sum of its digits 3+0=3 is evenly divisible by 3.
By 4: Number 30 is not evenly divisible by 4 because last two digits do not form number evenly divisible by 4.
By 5: Number 30 is evenly divisible by 5 because it ends with 0.
By 6: Number 30 is evenly divisible by 6 because it is divisible by 2 and by 3.
By 7: Number 30 is not evenly divisible by 7 because 3-2⋅0=3 is not divisible by 7.
By 8: Number 30 is not evenly divisible by 8 because 30÷8=3 r. 6. For this number it is more appropriate to divide the number by 8.
By 9: Number 30 is not evenly divisible by 9 because the sum of its digits 3+0=3 is not evenly divisible by 3.
By 10: Number 30 is evenly divisible by 10 because it ends with 0.
Ways of finding factors of a number
There are three main methods of finding factors of a number:
- division method;
- multiplication method;
- prime factorization method.
DIVISION METHOD: the division method is to find all divisors from 1 to the number itself that divide the number without remainder.
MULTIPLICATION METHOD: the multiplication method is to write the number as a product of two numbers in different possible ways.
PRIME FACTORIZATION METHOD: the prime factorization method is to express a composite number as the product of its prime factors.
Division method of finding the factors of 30
From the example, number 30 has more than two factors, so it is a composite number.
We can use division to find all positive factors of 30 (start with 1, then check 2, 3, 4, 5, 6 etc. up to 15 (number 15 is exactly half of 30) and the number 30 itself):
30÷1=30
30÷2=15
30÷3=10
30÷4=7 r.2
30÷5=6
30÷6=5
30÷7=4 r.2
30÷8=3 r.6
30÷9=3 r.3
30÷10=3
30÷11=2 r.8
30÷12=2 r.6
30÷13=2 r.4
30÷14=2 r.2
30÷15=2
30÷30=1
Therefore, 30 has a total of 8 positive factors: 1, 2, 3, 5, 6, 10, 15 and 30.
Multiplication method of finding the factors of 30
Represent the number 30 as a product of two numbers in all different possible ways:
30= 1 × 30
30= 2 × 15
30= 3 × 10
30= 5 × 6
All the numbers that are used in these products are the factors of 30. Thus, the positive factors of 30 are 1, 2, 3, 5, 6, 10, 15 and 30.
Prime factorization method of finding the factors of 30
Prime factorization is a way of expressing a number as a product of its prime factors. For example,
30=10×3
is not the prime factorization of 30 as number 10 is not a prime number.
Representation
30=2×3×5
is the prime factorization of 30 as numbers 2, 3 and 5 are prime numbers.
There are two possible ways to express number as a product of prime factors:
- division method;
- factor tree method.
PRIME FACTORIZATION USING DIVISION METHOD
The division method can be used to find the prime factors of a number by dividing the number by prime numbers. To find the prime factors of a number using the division method complete the next steps:
STEP 1: Evenly divide the number by the smallest possible prime number.
STEP 2: Evenly divide the quotient of step 1 by the smallest possible prime number.
STEP 3: Repeat step 2, until the quotient becomes 1.
LAST STEP: Multiply all the prime factors that are the divisors.
EXAMPLE: Write the prime factorization of the number 30 using the division method.
SOLUTION:
STEP 1: The smallest possible prime number that evenly divides 30 is number 2. Divide 30 by 2:
30 ÷ 2=15
STEP 2: The smallest possible prime number that evenly divides the quotient 15 is number 3. Divide 15 by 3:
15 ÷ 3=5
STEP 3: The smallest possible prime number that evenly divides the quotient 5 is number 5. Divide 5 by 5:
5 ÷ 5=1
LAST STEP: Multiply all the prime factors that are the divisors:
30=2×3×5
REMARK: Typically, this factorization is performed using a table in which only the simple factors and the corresponding fractions are recorded.
| 2 | 30 |
| 3 | 15 |
| 5 | 5 |
| 1 |
Prime factorization of 30=235
PRIME FACTORIZATION USING FACTOR TREE METHOD
A factor tree is a special diagram, where we draw the factors of a number, then the factors of those factors and so on until we get only prime factors.
EXAMPLE: Draw a factor tree for the number 30.
SOLUTION: From the multiplication table we know that 30=56. Therefore,
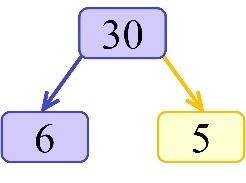
One of these numbers we can represent as a product of prime numbers:
6=2×3
So, the final factor tree is
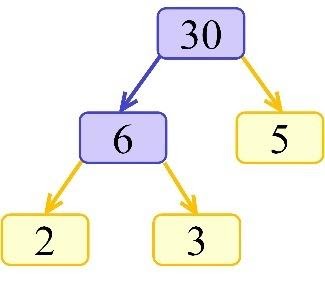
and the prime factorization of 30 is 2×3×5.
REMARK: You can start with arbitrary numbers giving 30 in product, but the final product must be always the same as the prime factorization is unique. For example, you can draw the following two factor trees for the number 30
and see that that the prime factorizations for all factor trees are the same. This is provided by the Fundamental Theorem of Arithmetic which states that
every natural number greater than 1 can be written as a product of prime numbers, and that up to rearrangement of the factors, this product is unique.
To find the prime factors of a number using the factor tree method complete the next steps:
STEP 1: Draw a factor tree starting from arbitrary numbers with product equal to the given number but finishing with only prime numbers.
STEP 2: Multiply all the prime factors that appear in this factor tree.
The method of finding the factors of a number using the prime factorization of the number is to multiply arbitrary combinations of prime factors.
EXAMPLE: The prime factorization of 30 is 2×3×5. Write down all positive factors of 30 using the prime factorization method.
SOLUTION: To write down all the factors and not lose any, use the following guidance of writing combinations:
- first, write down all possible powers of the first prime factor (starting with exponent of 0 and finishing with the maximum possible exponent defined in the prime factorization of the number):
20=1, 21=2
- then write down all possible powers of the second prime factor (starting with exponent of 0 and finishing with the maximum possible exponent defined in the prime factorization of the number):
30=1, 31=3
- then write down all possible powers of the second prime factor (starting with exponent of 0 and finishing with the maximum possible exponent defined in the prime factorization of the number):
50=1, 51=5
- now write all possible products of powers of two factors
21 x 31=6, 21 x 51=10, 31 x 51=15
- and, finally, the product of all three factors
21 x 31 x 51=30
Therefore, the list of all 8 positive factors of 30 written in ascending order is
1, 2, 3, 5, 6, 10, 15, 30
You can see that numbers 2, 3 and 5 are prime factors of 30.
Finding the number of positive factors
Using the prime factorization of a number, we can find the number of factors of this number. To do this, complete the following steps:
STEP 1: Write the prime factorization of a number in the exponent form.
STEP 2: Add one to each of the exponents.
STEP 3: Multiply all obtained numbers. This product denotes the number of factors of a number.
EXAMPLE: Find the number of factors of 30.
SOLUTION: From the previous topic, the prime factorization of the number 30 is 2×3×5. In exponent form this factorization is 21 x 31 x 51.
Add 1 to each exponent:
1+1=2
1+1=2
1+1=2
and multiply the obtained sums:
2×2×2=8
Therefore, the number of factors of 30 is 8.
Positive factor pairs of 30
A factor pair of a number is a set of two factors, which, when multiplied, give this number as a product. For example, factors 8 and 6 form a factor pair of 48 because
48=8×6
EXAMPLE: List all factor pairs of 30.
SOLUTION: Start with 1. Since 30=1×30, put 1 at the beginning of the list and 30 at the end of the list. Factors 1 and 30 form the first factor pair of 30.
| 1 | 30 |
Now, try 2. Since 30=2×15, put 2 at the beginning of the list (after 1) and 15 at the end of the list (before 30). Factors 2 and 15 form the second factor pair of 30.
| 1 | 2 | 15 | 30 |
Then, try 3. Since 30=3×10, put 3 at the beginning of the list (after 2) and 10 at the end of the list (before 15). Factors 3 and 10 form the third factor pair of 30.
| 1 | 2 | 3 | 10 | 15 | 30 |
At last, try 5. Since 30=56, put 5 at the beginning of the list (after 3) and 6 at the end of the list (before 10). Factors 5 and 6 form the last fourth factor pair of 30.
| 1 | 2 | 3 | 5 | 6 | 10 | 15 | 30 |
As there are no more whole factors of 30 between 5 and 6, we are done!
We can graphically represent positive factor pairs as shown below.
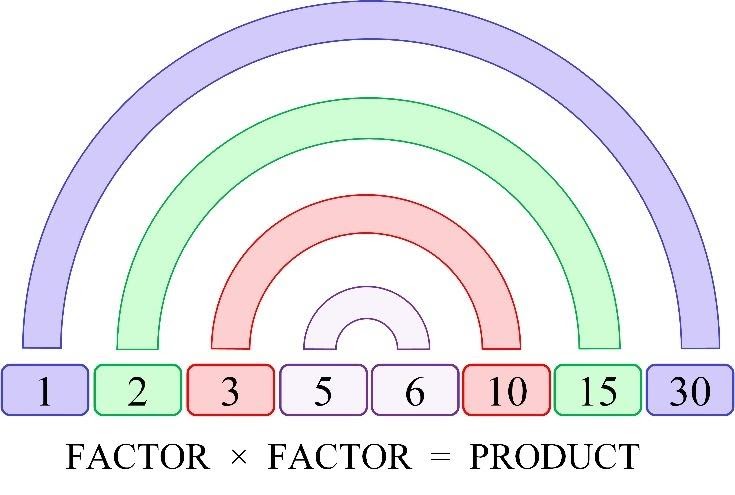
We could also add factor pairs 6, 5, 10, 3, 15, 2, (30 ,1) to the list, but multiplication is commutative, so meaning the order of numbers does not matter – you get the same result.
Negative factors of 30
From the previous topic we know there are 4 positive factor pairs of 30. These pairs are 1, 30,
(2, 15), (3, 10) and 5, 6.
If we note that the product of two negative numbers gives a positive number, then the same pairs of negative numbers will also be factor pairs.
Therefore, 4 negative factor pairs are
-1 and -30
-2 and -15
-3 and -10
-3 and -10
and list of negative factor pairs is
| -1 | -2 | -3 | -5 | -6 | -10 | -15 | -30 |
Here two numbers colored in one color form a negative factor pair.
Also, we can graphically represent negative factor pairs in the same way as graphical representation of positive factor pairs.
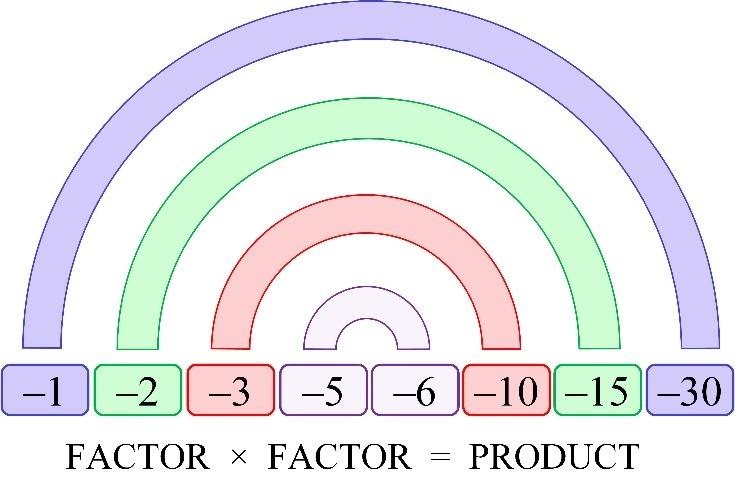
Quiz
- Answer the questions.
a) What is the greatest difference between two factors of 30?
b) What is the smallest positive difference between two factors of 30?
c) What is the smallest difference between two factors of 30?
SOLUTION: a) The greatest difference is between the greatest and the smallest factors. The greatest factor is 30, the smallest factor is … -30 (not 1 as you can think, we do not talk only about positive factors here). So, the greatest difference is
30-(-30)=60
b) The smallest positive difference is between two closest factors. Two closest factors are 5 and 6, so the smallest positive difference is
6-5=1
c) The smallest difference is between the smallest and the greatest factors. The greatest factor is 30, the smallest factor is -30. So, the smallest difference is
-30-30=-60
ANSWER: a) 60, b) 1, c) -60
- a) Can you come up with a divisibility rule by 12? Is 30 evenly divisible by 12?
b) Can you come up with a divisibility rule by 15? Is 30 evenly divisible by 15?
SOLUTION: a) We know that 12 is a product 3 and 4. So, the divisibility rule by 12 is
“Number is divisible by 4 and by 3”
Number 30 is evenly divisible by 3 but not evenly divisible by 4, so it is not evenly divisible by 12.
b) We know that 15 is a product 3 and 5. So, the divisibility rule by 15 is
“Number is divisible by 3 and by 5”
Number 30 is evenly divisible by 3 and by 5, so it is evenly divisible by 15.
ANSWER: a) No, b) Yes
- There are 30 singers in the choir. The choir kapellmeister wants to place them in a certain number of rows so that each row has the same number of singers and no singer is left. How many different ways can the kapellmeister do this?
SOLUTION: To determine the number of rows so that each row contains the same number of singers, we need to find all factors of the number of singers. From the article we know that 30 has 8 positive factors: 1, 2, 3, 5, 6, 10, 15, 30. Fill in the following table:
| Number of rows | Number of singers per row |
| 1 | 30÷1=30 |
| 2 | 30÷2=15 |
| 3 | 30÷3=10 |
| 5 | 30÷5=6 |
| 6 | 30÷6=5 |
| 10 | 30÷10=3 |
| 15 | 30÷15=2 |
| 30 | 30÷30=1 |
It is up to the kapellmeister to determine whether to place singers for example in 30 rows of 1 singer, but formally he has 8 different options for the arrangement of choristers.
ANSWER: 8 different arrangements
- Which of the following statements is true?
a) Number 30 has only prime factors.
b) Number 30 is 4 composite factors.
c) Numbers -2 and 15 form a factor pair of 30.
SOLUTION: a) Number 30 has 8 positive factors: 1, 2, 3, 5, 6, 10, 15, 30. Only three of them (2, 3, 5) are prime factors, so statement a) is false.
b) Number 30 has 8 positive factors: 1, 2, 3, 5, 6, 10, 15, 30. Four of them (6, 10, 15, 30) are composite numbers, so statement b) is true.
c) Statement c) is false because -2×15=-30 not 30.
ANSWER: a) False
b) True
c) False
- CHALLENGE QUESTION: How many different cuboids with volume of 30 un3. can be made from the same cubes with side of 1 un.?
SOLUTION: From the article, the prime factorization of 18 is 2×3×5. Then, the cuboids could be
1 un. × 1 un. × 30 un.

1 un. × 2 un. × 15 un.

1 un. × 3 un. × 10 un.
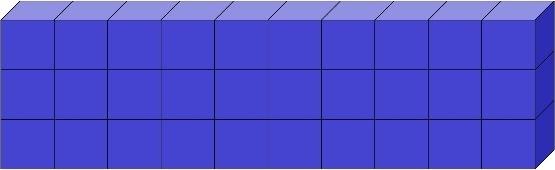
1 un. × 5 un. × 6 un.
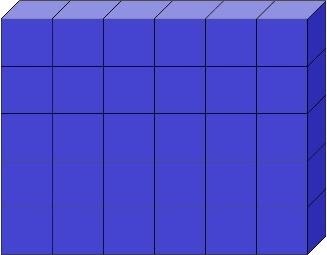
2 un. × 3 un. ×5 un.

ANSWER: 5 different cuboids
Conclusions
- Number 30 is composite number (it has more than two factors).
- Prime factors of 30 are 2, 3, 5.
- Number 30 has 8 positive factors: 1, 2, 3, 5, 6, 10, 15, 30 and 8 negative factors: -1, -2, -3, -5, -6, -10, -15, -30.
- 8 positive factors of 30 form 4 factor pairs as well as 8 negative factors.
- There are only 4 different factor trees of number 30.
Recommended Worksheets
Prime Numbers (Diwali Themed) Math Worksheets
Prime and Composite Numbers (Halloween Themed) Worksheets
Prime and Composite Numbers 4th Grade Math Worksheets