Introduction
When we perform operations involving multiplication or division, we often encounter the term “factors.” But what does this mean? How is this relevant for our arithmetic operations? We will learn about factors in this article and discover more about their properties, types, and how we can find them.
Factors
What are Factors?
A Factor is a number that divides another number without remainders. We can say that a factor is also a divisor of any number such that its quotient is a whole number.
We also recall that for a multiplication operation between two numbers a and b, we have both multiplicand and multiplier:
a×b=ab
In this operation, both a and b are considered factors of the product ab, since dividing the product by either number will result to the other number.
Let us now consider an example using the number 20. If we divide 20 by another number, let’s say 4, we have the following equation:
20÷4=5
Since 4 divides 20 into 5 without any remainder, we can say that the number 4 is a factor of 20.
Conversely, if we multiply 4 and 5 we can get the number 20 as their product:
4×5=20
Hence, we can say that both numbers 4 and 5 are factors of 20.
Properties of Factors
There are also some properties that we observe with factors:
First, all integers have a finite number of factors. This means that we can list down every factor of any given integer.
Second, any given number’s factor is always less than or equal to its value.
Third, any number has the number 1 as a factor.
Fourth, any natural number has itself as its factor.
In relation to the previous properties, any integer except from 0 and 1 has at least two factors: the number 1 and the number itself.
Types of Factors
Furthermore, we can also classify factors into two different types: prime factors and composite factors:
Prime Factors are numbers that only have two factors: the number itself and 1. Some examples are the numbers listed below:
2, 3, 5, 7, 11, 13, 17, 19
Composite Factors, on the other hand, are numbers that have more than two factors. This is because composite numbers can be broken down into prime factors. Some examples are the numbers listed below:
4, 6, 8, 9, 10, 12, 14, 15
Factor Pairs
When we refer to factor pairs, we mean two factors that make up a number when multiplied together. Let us consider the number 24. What pair of factors can we use to get this product?
24×1=24
We see that we can multiply the numbers 24 and 1 to get a product of 24. Hence, we say that 24 and 1 is a factor pair of 24.
But there can be more than one factor pair for this number, as we see below:
12×2=24
8×3=24
4×6=24
In these equations, we see the following factor pairs of 24: 12 and 2, 8 and 3, 4 and 6.
How to Find Factors
Now, we wish to find the factors of any number. To do this, we have multiple ways to determine whether a number is a factor: by multiplication, division, or by factorization using factor trees.
Multiplication
When we perform factorization using multiplication, we take one number and check if the number we are factoring is a multiple of the said number. If we find a multiple that is equal to the number we are factoring, then we say that it is indeed a factor.
As an example, we want to find a factor of 30 and we wish to check if the number 3 is a factor.
By going through the multiples of 3, we see that 30 is one of its multiples:
3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, …
In particular, we have the following multiplication operation that makes up 30:
3×10=30
Therefore, we conclude that 3 is a factor of 30.
But what happens if a number is not a factor? Let’s check whether the number 4 is a factor of 30:
4, 8, 12, 16, 20, 24, 28, 32, 36, 40, …
By listing the multiples of 4, we see that the closest numbers to 30 that are multiples of 4 are the numbers 28 and 32:
4×7=28
4×8=32
Hence, we see that 30 is not a multiple of 4, and thus the number 4 is not a factor of 30.
As a side note, familiarizing ourselves with multiplication tables and multiples of numbers helps find factors using multiplication.
Division
When we perform factorization using division, we pick one number and check whether the number we have chosen is a divisor of the number we are factoring. If there is no remainder in the quotient, then we say that that number is a factor.
We consider an example where we want to find a factor of 25. We choose the number 5 and check whether it is a factor of 25:
25÷5=5
Since the quotient is a whole number and there is no remainder, we know that the number 5 is a divisor of 25. Therefore, we conclude that 5 is a factor of the number 25.
Let’s consider another number 2 and check if it is a factor of 25:
25÷2=12 remainder 1
We note that the quotient obtained has a remainder of 1. Hence, we know that 2 is not a divisor of 25 and ft is not a factor of 25.
To master this method, it is recommended to remember rules on the divisibility of numbers to know quickly if a number is a divisor.
Factor Tree
We can also perform the factorization of numbers using a more visual approach. A factor tree is a diagram listing a number’s factors by up to its prime factors. We construct a factor tree by finding possible factors of a number and then splitting it into two branches containing its factors.
To better understand how we can make factor trees, let’s think of the number 56 and construct a factor tree. We begin by writing the number and we think of a number that is a divisor of 56. Let’s try the number 14:
56÷14=4
Since 14 divides 56 into 4, we can write both numbers below 56 in our factor tree:
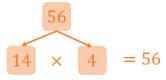
Next, we consider the factor 14 and check if we can still divide it into two factors. In this case, we consider the number 7:
14÷7=2
Since 7 divides 14 into 2, we can write both numbers below 14 in our factor tree:
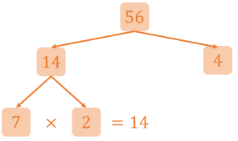
We know that 7 and 2 are prime factors, hence we do not branch further under these factors.
Next, we consider the number 4. We can divide this number into 2 such that:
4÷2=2
Thus, we write the factors below the number 4 in our factor tree:
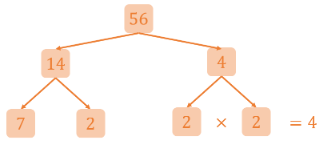
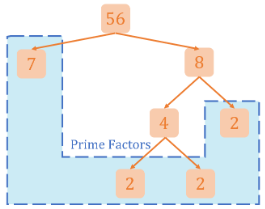
Therefore, we have the completed factor tree listing the factors of 56. We observe that the ends of the factor tree are all prime factors of the number 56. In fact, if we multiply all prime factors we arrive at the original number!
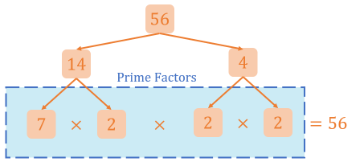
The process of getting the list of prime factors of a number is called prime factorization. This follows that constructing a factor tree is also a method for prime factorization of numbers.
It is also important to note that there can be more than one way of constructing factor trees. This depends on the initial choice of divisors that will make up the primary branches of our factor tree.
For example, another factor tree can be made for the number 56, where we choose 8 as the first divisor:
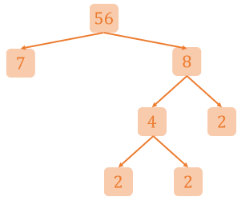
We made a different structure for this second factor tree. However, we can see that the list of prime factors remains the same:
Problem-Solving Examples
We can now proceed to solve sample problems to apply what we have learned so far. Each problem tackles different techniques discussed and gives us a challenge on how to solve through the information given to us.
Finding Factors Using Multiplication
Sample Problem 1:
What are the factors of 60?
Solution:
We know from the properties of factors that there are at least two factors of 60: 1 and 60. This is shown in the equation below:
1 x 60=60
Next, we check the number 2 and check the multiples of 2:
2×30=60
Since 60 is a multiple of 2, we confirm that 2 is a factor of 60.
Moreover, by the Commutative Property of Multiplication we can also show that 30 is a factor of 60:
30×2=60
Next, we check the number 3 and its multiples:
3×20=60
Since 60 is a multiple of 3, we confirm that 3 is a factor of 60.
Commutatively, we can show that 20 is a multiple of 60:
20×3=60
By repeating the same manner for bigger numbers, we can find the following factor pairs using multiplication:
4×15=15×4=60
5×12=12×4=60
6×10=10×6=60
Therefore, the factors of 60 are the following numbers:
{1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60}
Sample Problem 2:
A farmer wants to pack 100 onions into equal groups. In how many ways can he pack these onions?
Solution:
We are given 100 onions that need to be packed equally, and we are asked how many ways this can be done. We can think of the problem as finding how many factor pairs the number 100 has. Hence, we will explore the factors of 100 using multiplication.
We know from the properties of factors that the first factor pair is given by its first two factors: 1 and 60. This is shown in the equation below:
1 x 100=100
Next, we consider the number 2 and check whether 100 is a multiple of 2:
2×50=100
Since 100 is a multiple of 2, we confirm that 2 is a factor of 100.
Moreover, by the Commutative Property of Multiplication we can also show that 50 is a factor of 100:
50×2=100
Hence, we know that 2 and 50 is a factor pair of 100.
Similarly, we can check larger numbers as factor pairs by checking multiples and applying commutativity:
4×25=25×4=100
5×20=20×5=100
1010=100
Now, we can list the factor pairs we have found so far:
{1, 100}, {2, 50}, {4, 25}, {5, 20}, {10,10}, {20, 5}, {25, 4}, {50, 2}, {100, 1}
By counting the number of factor pairs, we have 9 pairs. Therefore, we conclude that the farmer can pack 100 onions equally in 9 ways listed below:
- 1 pack containing 100 onions,
- 2 packs containing 50 onions each,
- 4 packs containing 25 onions each,
- 10 packs containing 10 onions each,
- 20 packs containing 5 onions each,
- 25 packs containing 4 onions each,
- 50 packs containing 2 onions each,
- 100 packs containing 1 onion each
Finding Factors Using Division
Sample Problem 3:
What are the factors of 120?
Solution:
We know from the properties of factors that the first two factors of 120 are given by its first two factors: 1 and 120. This is shown in the equation below:
120÷1=120
120÷120=1
Then, we consider the number 2 and check if it is a divisor of 120:
120÷2=60
Since 2 divides 120 without any remainder, we conclude that the number 2 is a factor of 120.
Furthermore, if we interchange the positions of the quotient 60 and divisor 2, we can also show that 60 is a factor of 120:
120÷60=2
Similarly, we can check larger numbers if they are factors of 120 by dividing them and checking if there are no remainders:
| 120÷3=40 | 120÷40=3 |
| 120÷4=30 | 120÷30=4 |
| 120÷5=24 | 120÷24=5 |
| 120÷6=20 | 120÷20=6 |
| 120÷8=15 | 120÷15=8 |
| 120÷10=12 | 120÷12=10 |
Therefore, the factors of 120 are the following numbers:
{1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 40, 60, 120}
Sample Problem 4:
A group of girl scouts prepared 64 cookies for selling. How many ways can they put these cookies in boxes containing an equal number of cookies?
Solution:
We are given 64 cookies to be boxed equally, and we are asked how many ways this can be done. We can think of the problem as finding how many factor pairs the number 64 has. Hence, we will explore the factors of 64 by finding its divisors.
We know from the properties of factors that the first factor pair of 64 is given by its first two factors: 1 and 64. This is shown in the equation below:
64÷1=64
64÷64=1
Then, we consider the number 2 and check if it is a divisor of 64:
64÷2=32
Since 2 divides 64 without any remainder, we conclude that the number 2 is a factor of 64.
Furthermore, if we interchange the positions of the quotient 32 and divisor 2, we can also show that 32 is a factor of 64:
64÷32=2
Similarly, we can check larger numbers if they are factors of 120 by dividing them and checking if there are no remainders:
64÷4=16
64÷16=4
64÷8=8
Now, we can list the factor pairs we have found so far:
{1, 64}, {2, 32}, {4, 16}, {8, 8}, {16, 4}, {32, 2}, {64, 1}
By counting the number of factor pairs, we have 7 pairs. Therefore, we conclude that the group of girl scouts can box 64 cookies equally in 7 ways listed below:
- 1 box with 64 cookies,
- 2 boxes with 32 cookies each,
- 4 boxes with 16 cookies each,
- 8 boxes with 8 cookies each,
- 16 boxes with 4 cookies each,
- 32 boxes with 2 cookies each,
- 64 boxes with 1 cookie each
Finding Factors Using Factor Trees
Sample Problem 5:
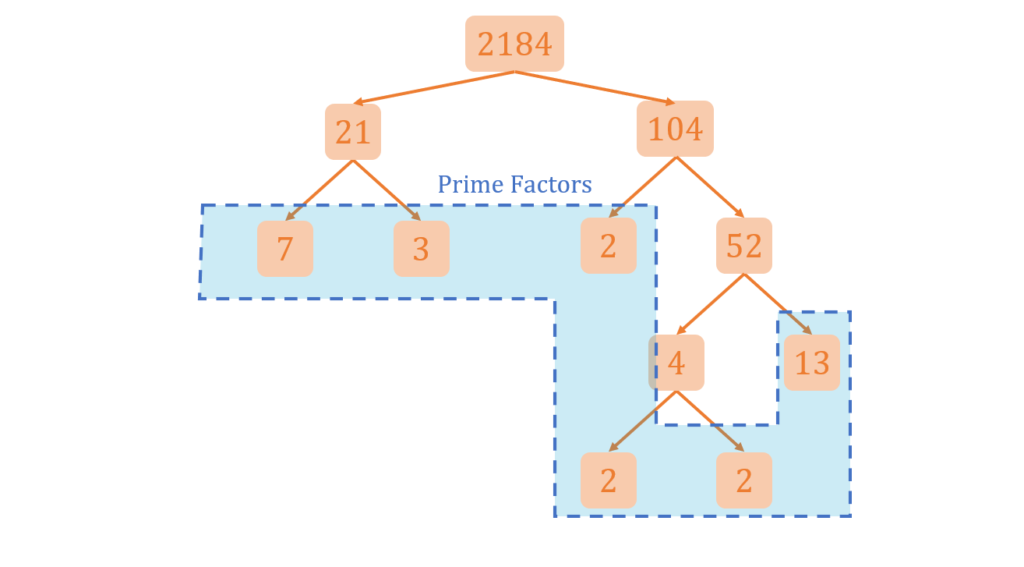
Perform prime factorization of the number 2184 through a factor tree.
Solution:
We first write the number and find a divisor of the number 2184. In this case, we consider the number 21:
7184÷21=104
Since 21 is a divisor of 7184, we can write 21 and the quotient 104 under the original number:

Next, we check whether the factor 21 can be further split into two factors:
21÷7=3
Since 7 is a divisor of 21, we can split the number 21 into 7 and the quotient 3:
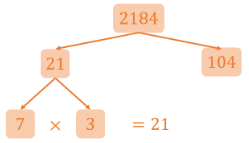
We observe that both are already prime factors, hence we can stop branching our factor tree and move to the next branch.
For the number 104, since it is an even number we can divide it by 2 to get a quotient of 52:
104÷2=52
Hence, we write both numbers under 104 in our factor tree. We note that 2 is already a prime factor so we do not need to branch further below that number:
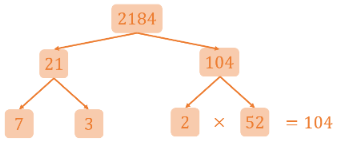
Then, we consider the factor 52. We can divide this by 4 to get a quotient of 13:
52÷4=13
Since both divisor and quotient are factors of 52, we write them under 52. We note that 13 is a prime factor:

Lastly, we take the number 4 and split it into two factors:
4÷2=2
We now finish the factor tree by writing the last two prime factors as shown:

Therefore, we can list the prime factors of 2184:
2184=7×3×2×2×2×13
Summary
A Factor is a number that divides another number without remainders. We can say that a factor is also a divisor of any number such that its quotient is a whole number.
There are also some properties that we observe with factors:
- First, all integers have a finite number of factors.
- Second, any given number’s factor is always less than or equal to its value.
- Third, any number has the number 1 as a factor.
- Fourth, any natural number has itself as its factor.
- Fifth, any integer except from 0 and 1 has at least two factors: the number 1 and the number itself.
Factors can be classified into two types:
Prime Factors are numbers that only have two factors: the number itself and 1.
Composite Factors, on the other hand, are numbers that have more than two factors. This is because composite numbers can be broken down into prime factors.
Factor Pairs are two factors of a number that, when multiplied, result to the number itself.
To find factors, we can use the following methods, multiplication, division, or factorization using factor trees:
When we perform factorization using multiplication, we take one number and check if the number we are factoring is a multiple of the said number.
When we perform factorization using division, we pick one number and check whether the number we have chosen is a divisor of the number we are factoring.
A factor tree is a diagram listing a number’s factors by up to its prime factors. By branching a number into its factors, we can also get the prime factorization of the given number.
Frequently Asked Questions (FAQs)
How do we know if a number is divisibly by 1?
Any number is divisible by 1. By the Identity Property of Division, any number divided by 1 results to the number itself.
How do we know if a number is divisibly by 2?
A number is divisible by 2 if it is an even number. This means any number ending in an even number is divisible by 2. We list below one-digit even numbers as a guide:
Even numbers: 0, 2, 4, 6, 8
How do we know if a number is divisibly by 3?
A number is divisible by 3 if the sum of its digits is a multiple of 3. For example, we consider the number 39. If we add its digits, we get the sum:
3+9=12
Then, we know that 12 is a multiple of 3. Therefore, the number 39 is divisibly by 3.
How do we know if a number is divisibly by 4?
A number is divisible by 4 if its last two digits is a multiple of 4. For example, we consider the number 128. If we check the last two digits 28, we know that it is a multiple of 4:
4×7=28
Therefore, the number 128, or any number ending in 28 is divisible by 4.
How do we know if a number is divisibly by 5?
A number is divisible by 5 if its last digit is either 5 or 0. For example, we list the following numbers ending in either 5 or 0 that are divisible by 5:
5, 10, 15, 20, 25, 100, 125, 150
How do we know if a number is divisibly by 10?
A number is divisible by 10 if its last digit is 0. For example, we list the following numbers ending in 0 that are divisible by 10:
10, 20, 30, 100, 150, 170, 1110, 12340
How do we know if a number is divisibly by a composite number?
To know whether a number is divisible by a composite number, we can check divisibility by its prime factors. For example, we wish to know if the number 120 is divisible by 6.
We know that the composite number 6 can be expressed as a product of its prime factors 3×2. Hence, we check if the number 120 is divisible by both 3 and 2.
Since the number 120 is an even number ending in 0, we know that it is divisibly by 2:
120÷2=60
Also, since the sum of the digits of the number 120 adds up to 3, we know that it is divisible by 3:
1+2+0=3
∴120÷3=20
Therefore, since 120 is divisible by both 3 and 2, we conclude that the number is divisible by 6.
Recommended Worksheets
Factorization (Amelia Earhart Day Themed) Math Worksheets
Factoring Simple Polynomials (International Nurses’ Day Themed) Math Worksheets
Divisibility Rules (Groundhog Day Themed) Math Worksheets









